Roc eğrisi nasıl yorumlanır (örneklerle)

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullandığımız istatistiksel bir yöntemdir. Lojistik regresyon modelinin bir veri kümesine ne kadar iyi uyduğunu değerlendirmek için aşağıdaki iki ölçüme bakabiliriz:

• Duyarlılık: Sonuç gerçekten olumluyken modelin bir gözlem için olumlu bir sonuç tahmin etme olasılığı.
• Özgüllük: Sonuç gerçekte negatif olduğunda modelin bir gözlem için negatif bir sonuç öngörme olasılığı.

Bu iki ölçümü görselleştirmenin basit bir yolu, lojistik regresyon modelinin duyarlılığını ve özgüllüğünü gösteren bir grafik olan ROC eğrisi oluşturmaktır.

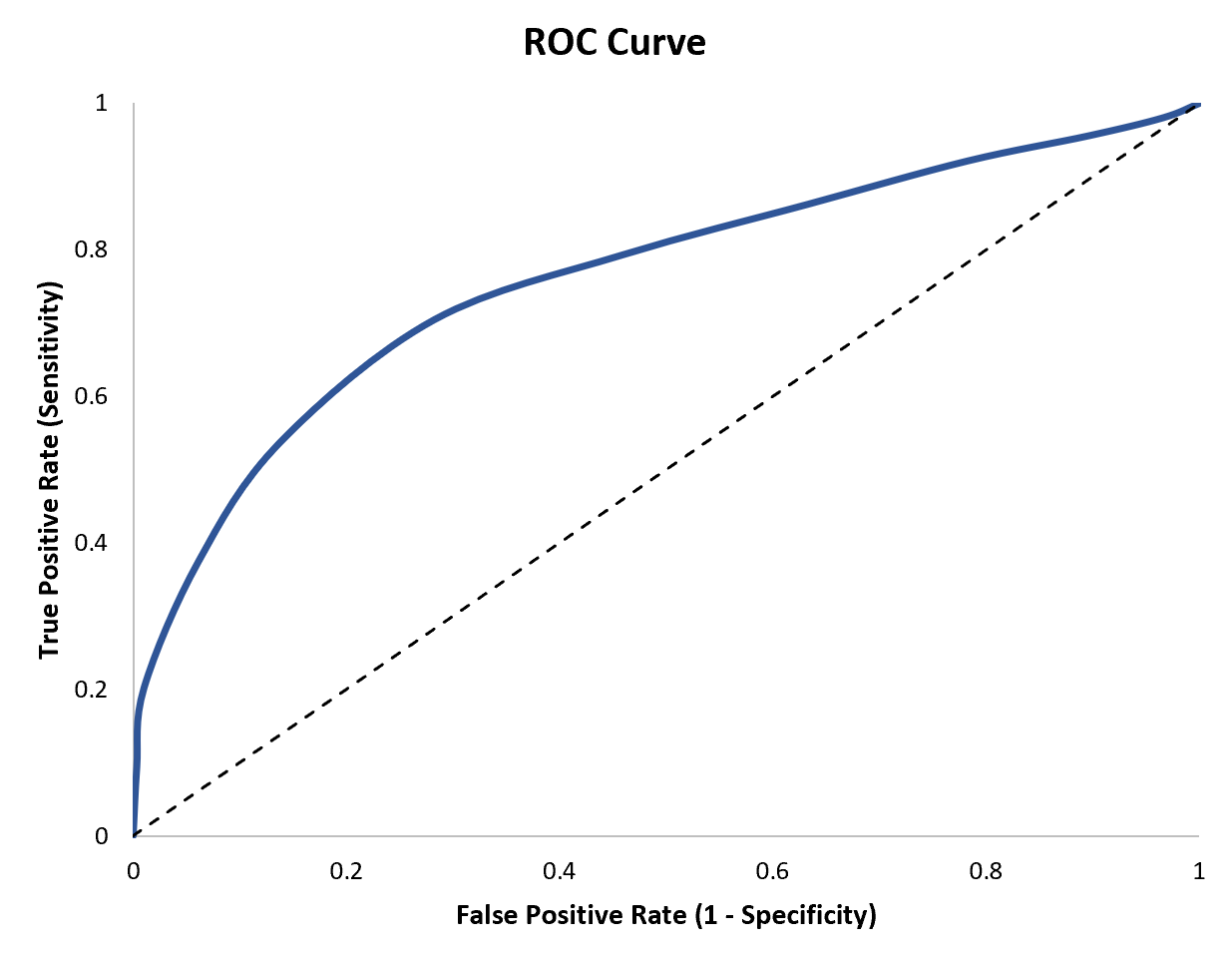
Bu eğitimde bir ROC eğrisinin nasıl oluşturulacağı ve yorumlanacağı açıklanmaktadır.

ROC Eğrisi Nasıl Oluşturulur

Lojistik regresyon modelini yerleştirdikten sonra bu modeli gözlemleri iki kategoriden birinde sınıflandırmak için kullanabiliriz.

Örneğin gözlemleri “olumlu” veya “olumsuz” olarak sınıflandırabiliriz.

Gerçek pozitif oran, gerçekte pozitif olması gereken gözlemlerin oranını temsil eder.

Tersine, yanlış pozitif oranı, pozitif olması gereken ancak gerçekte negatif olan gözlemlerin oranını temsil eder.

Bir ROC eğrisi oluşturduğumuzda, lojistik regresyon modelinin her olası karar eşiği için gerçek pozitif oran ile yanlış pozitif oran çiftlerini çizeriz.

ROC eğrisi nasıl yorumlanır?

ROC eğrisi grafiğin sol üst köşesine ne kadar yakın olursa, model verileri kategorilere göre o kadar iyi sınıflandırabilir.

Bunu ölçmek için, bize grafiğin ne kadarının eğrinin altında olduğunu söyleyen AUC’yi (eğrinin altındaki alan) hesaplayabiliriz.

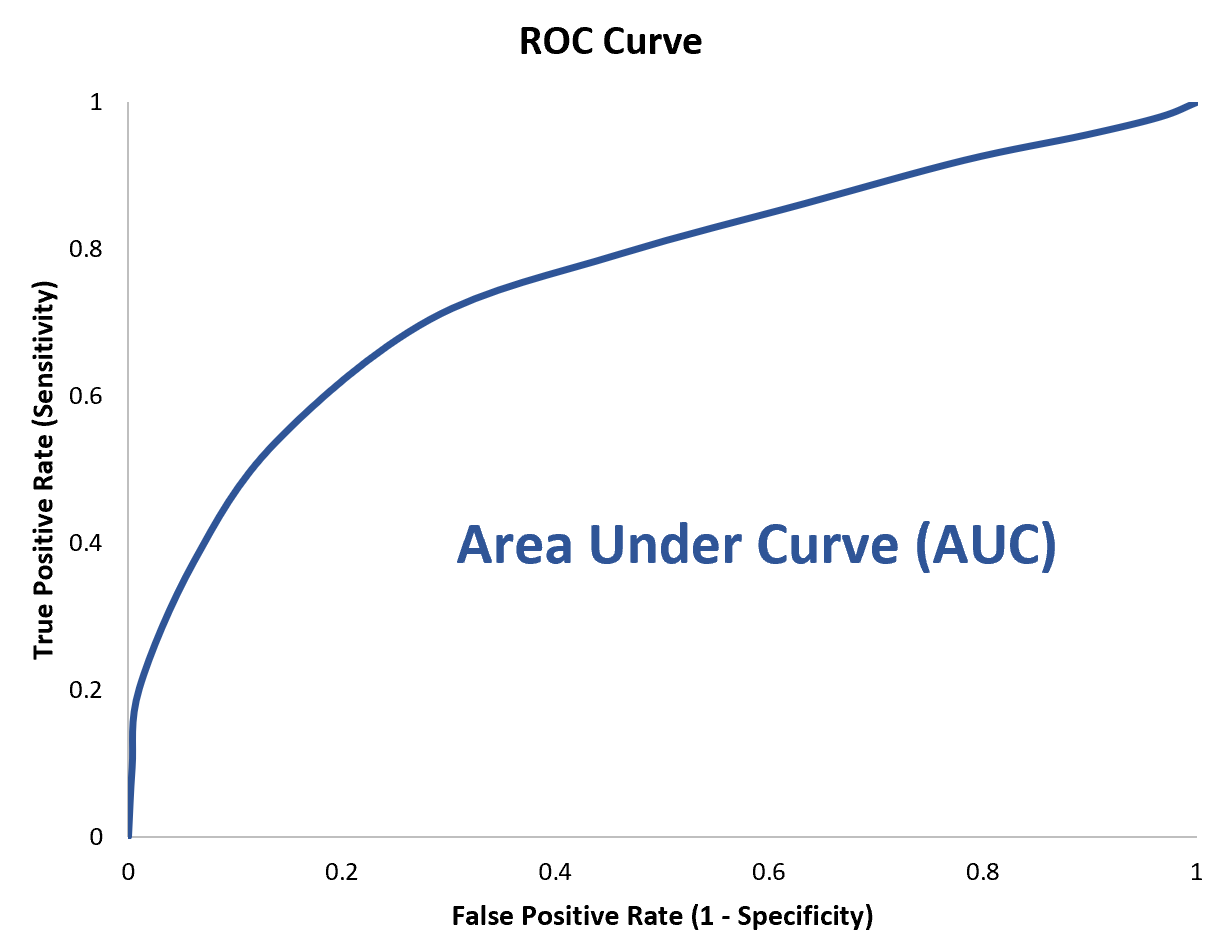
AUC 1’e ne kadar yakınsa model o kadar iyidir.

AUC değeri 0,5’e eşit olan bir model mükemmel bir çapraz çizgi olacaktır ve rastgele sınıflandırma yapan bir modelden daha iyi olmayan bir modeli temsil edecektir.

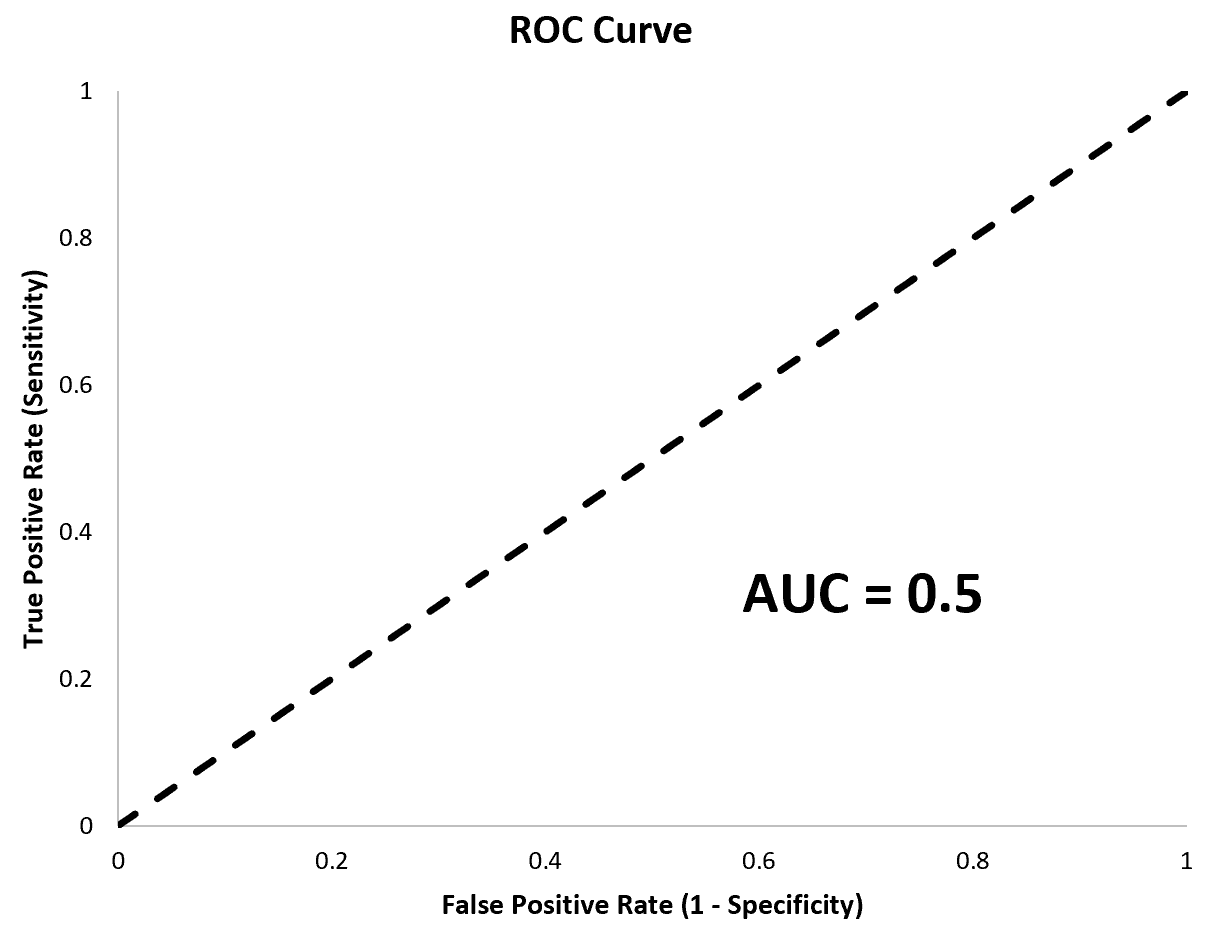
Çoklu lojistik regresyon modelleri için AUC’yi hesaplamak özellikle yararlıdır çünkü hangi modelin tahmin yapmada en iyi olduğunu görmemize olanak tanır.

Örneğin, üç farklı lojistik regresyon modeli uydurduğumuzu ve her model için aşağıdaki ROC eğrilerini çizdiğimizi varsayalım:

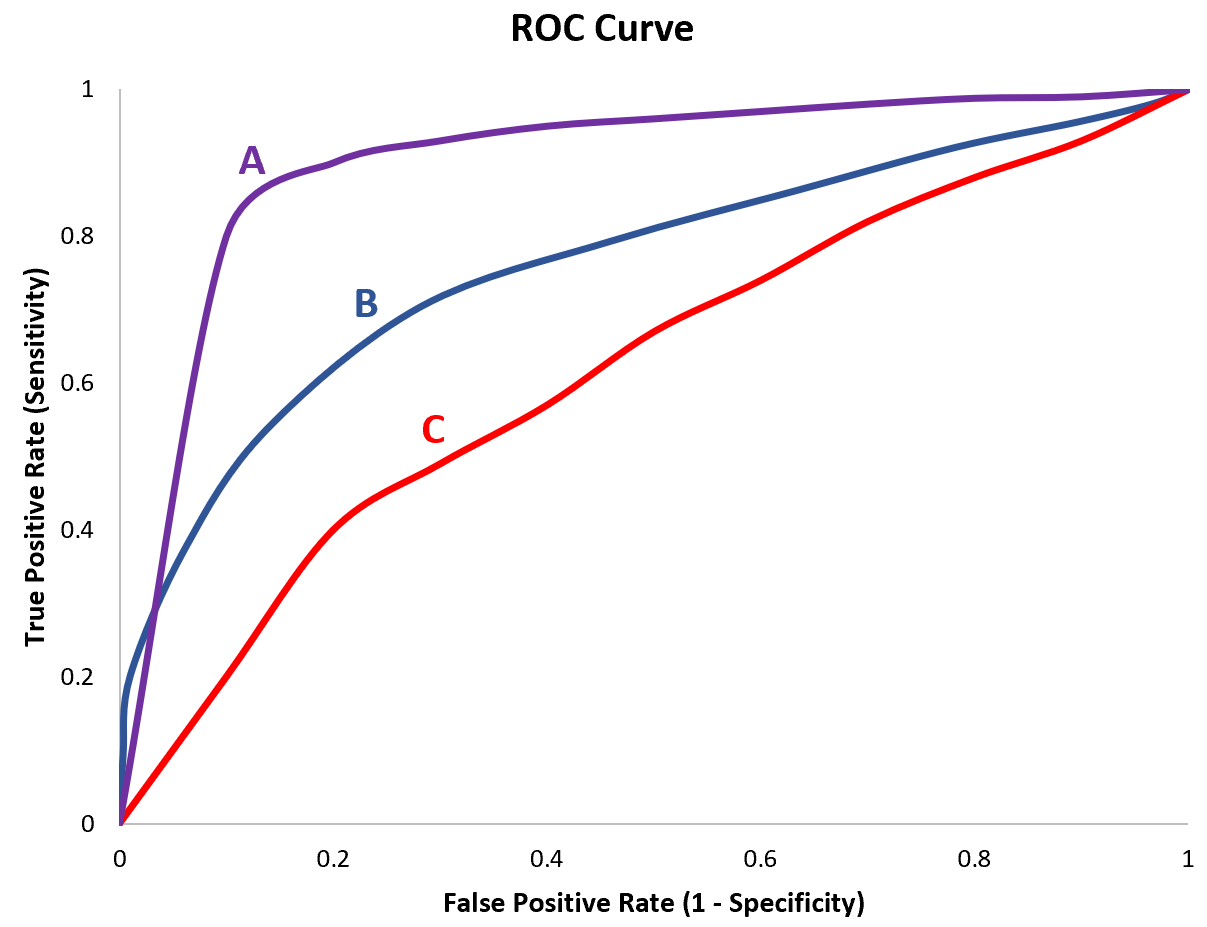
Her model için AUC’yi aşağıdaki şekilde hesapladığımızı varsayalım:

• Model A: AUC = 0,923
• Model B: AUC = 0,794
• Model C: AUC = 0,588

Model A, en yüksek AUC’ye sahiptir; bu, onun eğri altında en yüksek alana sahip olduğunu ve gözlemleri kategoriler halinde doğru bir şekilde sınıflandırmak için en iyi model olduğunu gösterir.

Ek kaynaklar

Aşağıdaki eğitimlerde farklı istatistiksel yazılımlar kullanılarak ROC eğrilerinin nasıl oluşturulacağı açıklanmaktadır:

• R’de bir ROC eğrisi nasıl çizilir
• Python’da bir ROC eğrisi nasıl çizilir
• Excel’de ROC Eğrisi Nasıl Oluşturulur
• SPSS’de ROC Eğrisi Nasıl Oluşturulur ve Yorumlanır
• Stata’da ROC eğrisi nasıl oluşturulur ve yorumlanır