Kendall's tau: tanım + örnek

İstatistikte korelasyon , iki değişken arasındaki ilişkinin gücünü ve yönünü ifade eder. Korelasyon katsayısının değeri -1 ile 1 arasında değişebilir; -1, mükemmel bir negatif ilişkiyi, 0, hiçbir ilişkinin olmadığını ve 1, mükemmel bir pozitif ilişkiyi belirtir.

En sık kullanılan korelasyon katsayısı, iki sayısal değişken arasındaki doğrusal ilişkiyi ölçen Pearson korelasyon katsayısıdır .

Daha az kullanılan bir korelasyon katsayısı, sıralanmış verilerin iki sütunu arasındaki ilişkiyi ölçen Kendall’s Tau’dur .

Genellikle τ olarak kısaltılan Kendall Tau’yu hesaplama formülü aşağıdaki gibidir:

τ = (CD) / (C+D)

Altın:

C = eşleşen çiftlerin sayısı

D = uyumsuz çiftlerin sayısı

Aşağıdaki örnek, sıralanmış verilerin iki sütunu için Kendall’ın Tau sıra korelasyon katsayısını hesaplamak amacıyla bu formülün nasıl kullanılacağını gösterir.

Kendall’s Tau’yu hesaplama örneği

İki basketbol koçunun oyuncularını en kötüden en iyiye doğru 12. sırada sıraladığını varsayalım. Aşağıdaki tabloda her antrenörün oyunculara atadığı sıralamalar gösterilmektedir:

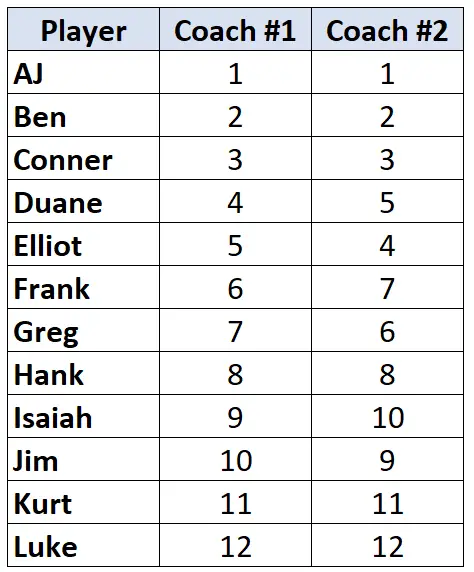
İki sütun dereceli veriyle çalıştığımızdan, iki antrenörün sıralaması arasındaki korelasyonu hesaplamak için Kendall’ın Tau’sunu kullanmak uygundur. Kendall’s Tau’yu hesaplamak için aşağıdaki adımları izleyin:

Adım 1: Eşleşen çiftlerin sayısını sayın.

Sadece 2 numaralı antrenörün sıralamasına bakın. İlk oyuncudan başlayarak, onun altındaki kaç sıranın daha uzun olduğunu sayın. Örneğin “1”in altında daha büyük 11 sayı var, dolayısıyla 11 yazacağız:

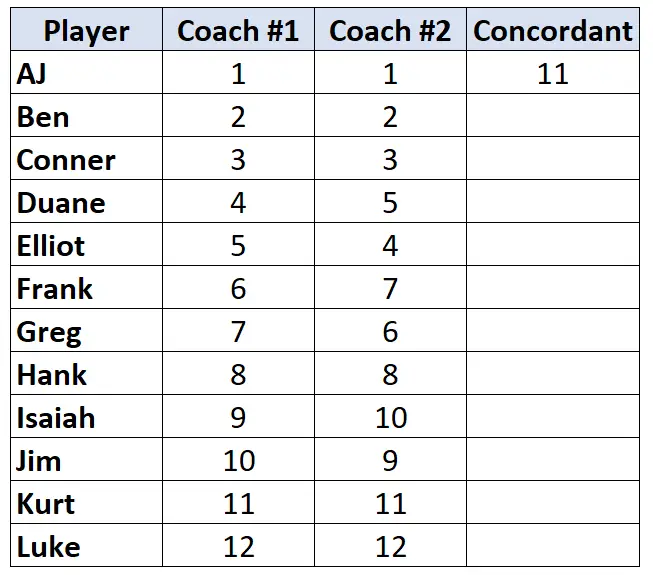
Bir sonraki oyuncuya geçin ve işlemi tekrarlayın. “2”nin altında daha büyük 10 sayı var, dolayısıyla 10 yazacağız:

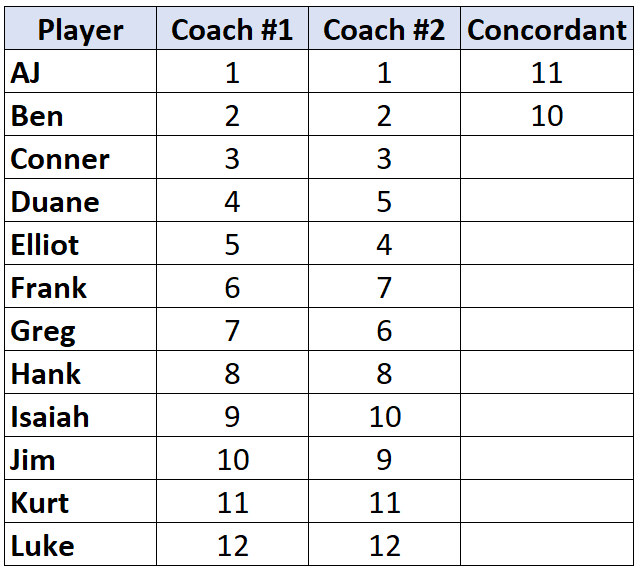
Sıralaması kendisinden önceki oyuncudan daha düşük olan bir oyuncuya ulaştığımızda, ona basitçe kendisinden önceki oyuncuyla aynı değer atanır. Örneğin, Elliot’ın sıralaması “4”tür ve bu, önceki oyuncunun “5” olan sıralamasından daha düşüktür, dolayısıyla kendisine, kendisinden önceki oyuncuyla aynı değer atanır:

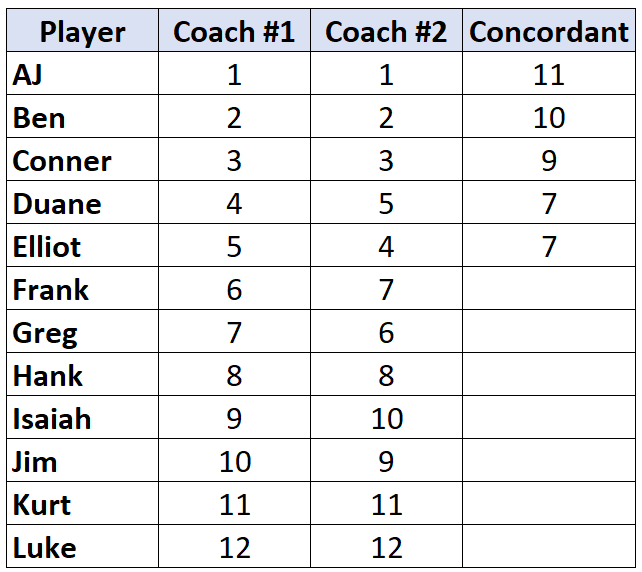
Bu işlemi tüm oyuncular için tekrarlayın:

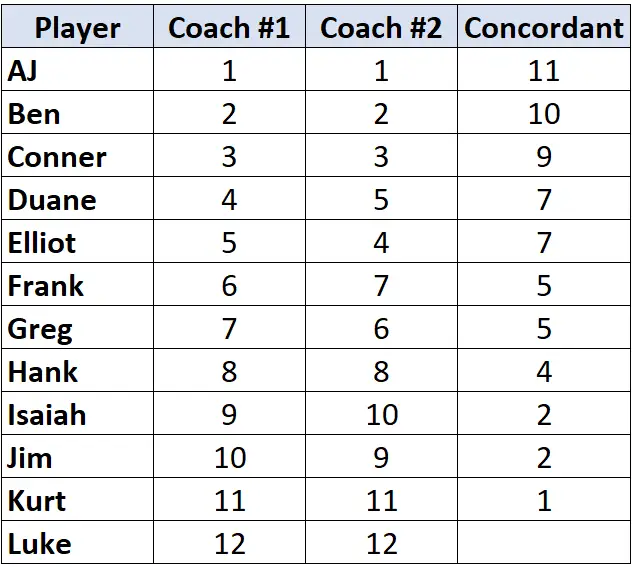
Adım 2: Uyumsuz çiftlerin sayısını sayın.

Tekrar ediyorum, sadece 2 numaralı Koçun sıralamasına bakın. Her oyuncu için, kendisinin altındaki kaç sıranın daha küçük olduğunu sayın. Örneğin, 2 numaralı Koç AJ’ye sıralamayı “1” olarak atadı ve onun altındaki hiçbir oyuncunun daha düşük bir sıralaması yok. Böylece ona 0 değerini atadık:

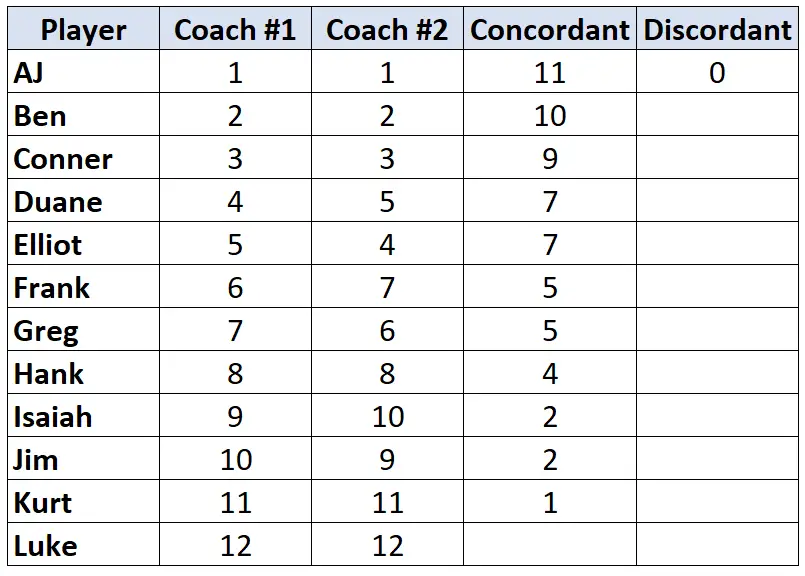
Bu işlemi her oyuncu için tekrarlayın:

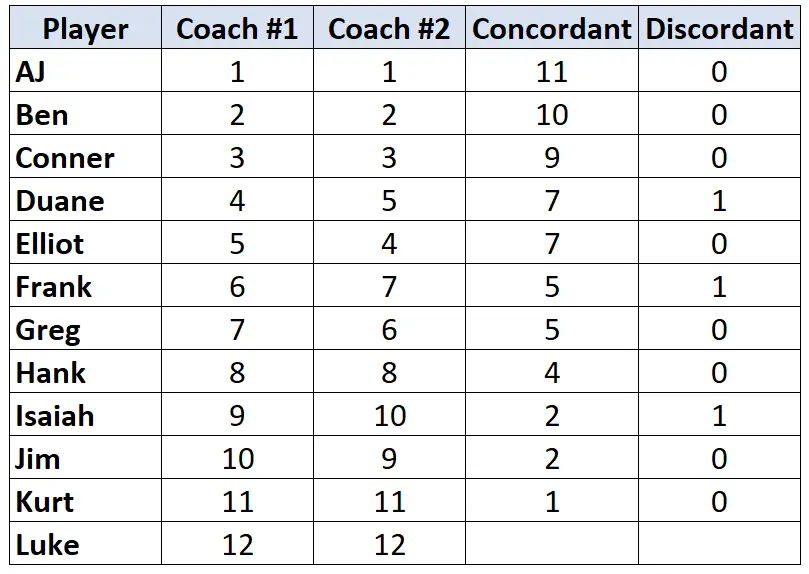
Adım 3: Her sütunun toplamını hesaplayın ve Kendall’ın Tau’sunu bulun.

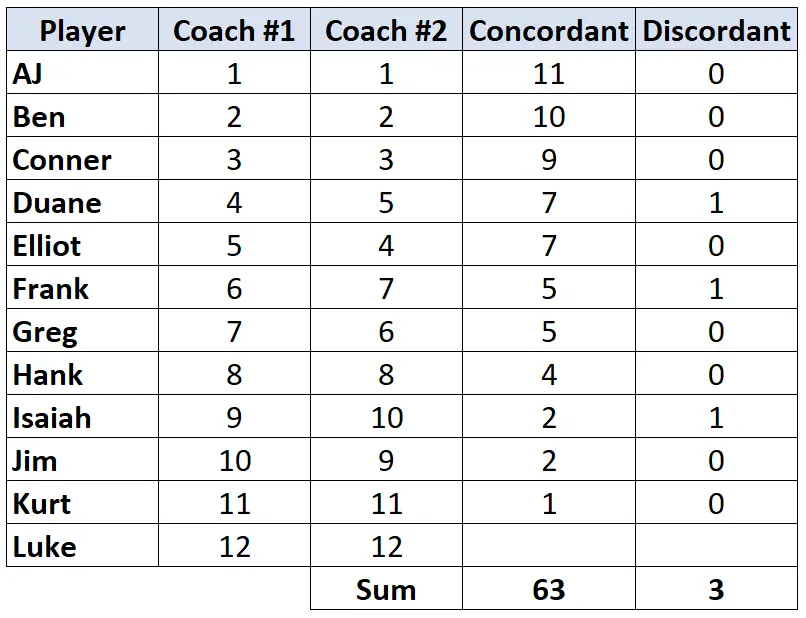
Kendall’ın Tau’su = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Kendall Tau’nun istatistiksel önemi

N=10’dan fazla çiftiniz olduğunda Kendall’s Tau genellikle normal bir dağılım izler. Kendall’s Tau’nun z-puanını hesaplamak için aşağıdaki formülü kullanabilirsiniz:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Altın:

τ = Kendall’s Tau için hesapladığınız değer

n = çift sayısı

Önceki örnek için z’nin nasıl hesaplanacağı aşağıda açıklanmıştır:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4,11 .

P-değeri Z-puanı hesaplayıcısını kullanarak, bu z-puanı için p-değerinin 0,00004 olduğunu ve bunun 0,05 alfa seviyesinde istatistiksel olarak anlamlı olduğunu görüyoruz. Dolayısıyla iki antrenörün oyunculara verdiği sıralamalar arasında istatistiksel olarak anlamlı bir korelasyon bulunmaktadır.

Bonus: R’de Kendall’s Tau nasıl hesaplanır?

R istatistik yazılımında, aşağıdaki sözdizimini kullanan iki vektör için Kendall Tau’sunu hesaplamak amacıyla VGAM kitaplığındaki kendall.tau() işlevini kullanabilirsiniz:

kendall.tau(x, y)

burada x ve y eşit uzunlukta iki dijital vektördür.

Aşağıdaki kod, önceki örnekte kullandığımız veriler için Kendall Tau’nun nasıl hesaplanacağını göstermektedir:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Kendall’ın Tau değerinin manuel olarak hesapladığımız değerle nasıl eşleştiğine dikkat edin.