Excel'de ortalama karekök hatası (rmse) nasıl hesaplanır?

İstatistikte regresyon analizi , yordayıcı değişken x ile yanıt değişkeni y arasındaki ilişkiyi anlamak için kullandığımız bir tekniktir.

Regresyon analizi yaptığımızda, yordayıcı değişkenin değerine bağlı olarak bize yanıt değişkeninin tahmin edilen değerini söyleyen bir model elde ederiz.

Modelimizin belirli bir veri kümesine ne kadar iyi uyduğunu değerlendirmenin bir yolu, tahmin edilen değerlerimizin gözlemlenen değerlerimizden ortalama olarak ne kadar uzakta olduğunu bize söyleyen bir ölçüm olan ortalama karesel hatanın hesaplanmasıdır.

Daha yaygın olarak RMSE olarak bilinen ortalama kare hatasını bulma formülü şöyledir:

RMSE = √[ Σ(P _ben – Ö _ben ) ² / n ]

Altın:

• Σ “toplam” anlamına gelen süslü bir semboldür
• P _i , veri kümesindeki ^i’inci gözlem için tahmin edilen değerdir
• _Oi veri kümesindeki ^i’inci gözlem için gözlemlenen değerdir
• n örneklem büyüklüğüdür

Teknik notlar :

• Ortalama kare hatası, tahmin edilen değerleri üreten herhangi bir model türü için hesaplanabilir ve bu daha sonra bir veri setinin gözlemlenen değerleriyle karşılaştırılabilir.
• Ortalama kare hatası bazen ortalama kare sapma olarak da adlandırılır ve genellikle RMSD olarak kısaltılır.

Daha sonra, Excel’de ortalama kare hatasının nasıl hesaplanacağına dair bir örneğe bakalım.

Excel’de Ortalama Kare Hatası Nasıl Hesaplanır?

Excel’de RMSE’yi hesaplamak için yerleşik bir işlev yoktur, ancak bunu tek bir formülle oldukça kolay bir şekilde hesaplayabiliriz. İki farklı senaryo için RMSE’nin nasıl hesaplanacağını göstereceğiz.

Senaryo 1

Bir senaryoda, modelinizden tahmin edilen değerleri içeren bir sütuna ve gözlemlenen değerleri içeren başka bir sütuna sahip olabilirsiniz. Aşağıdaki resimde bu senaryonun bir örneği gösterilmektedir:

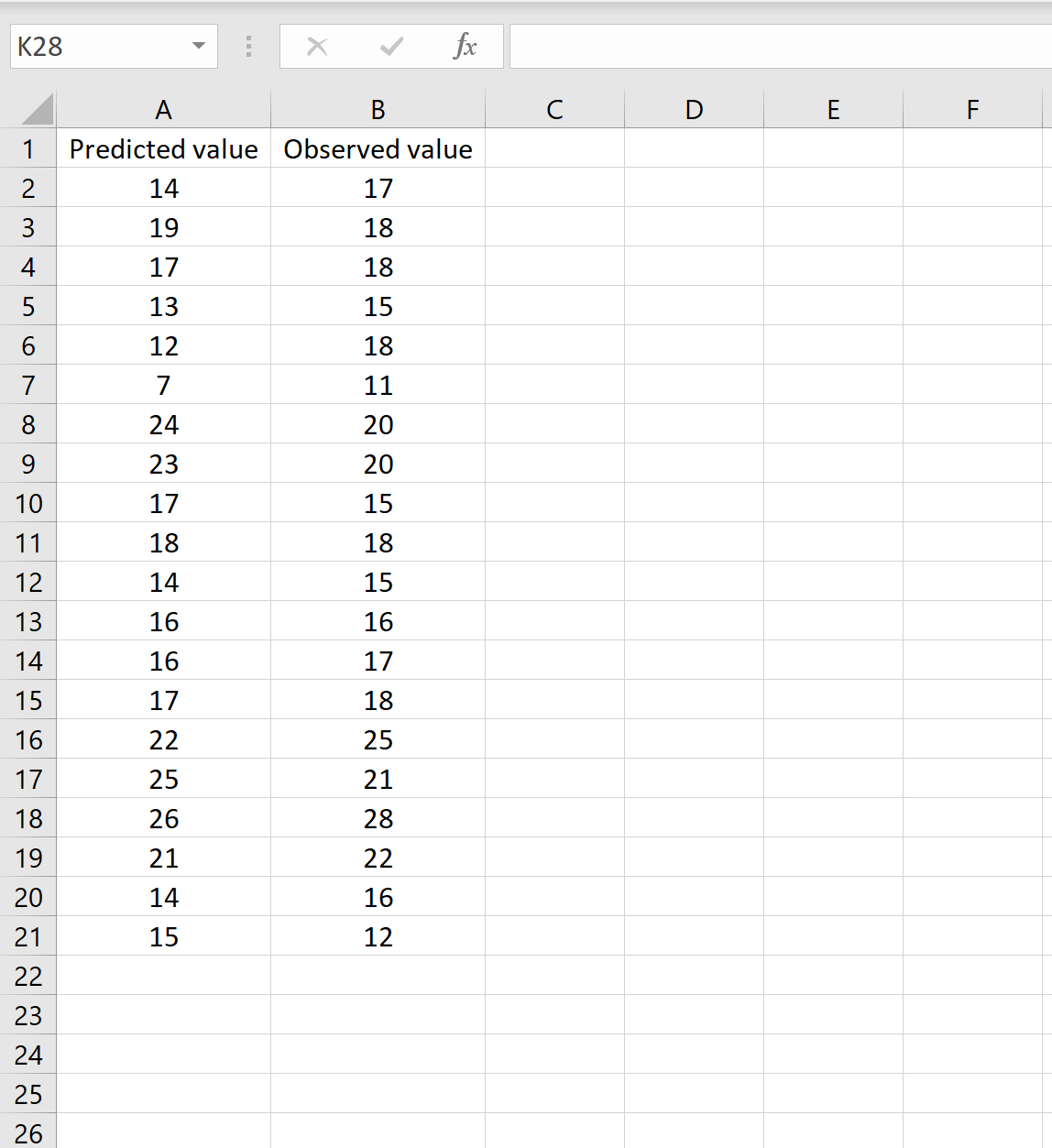
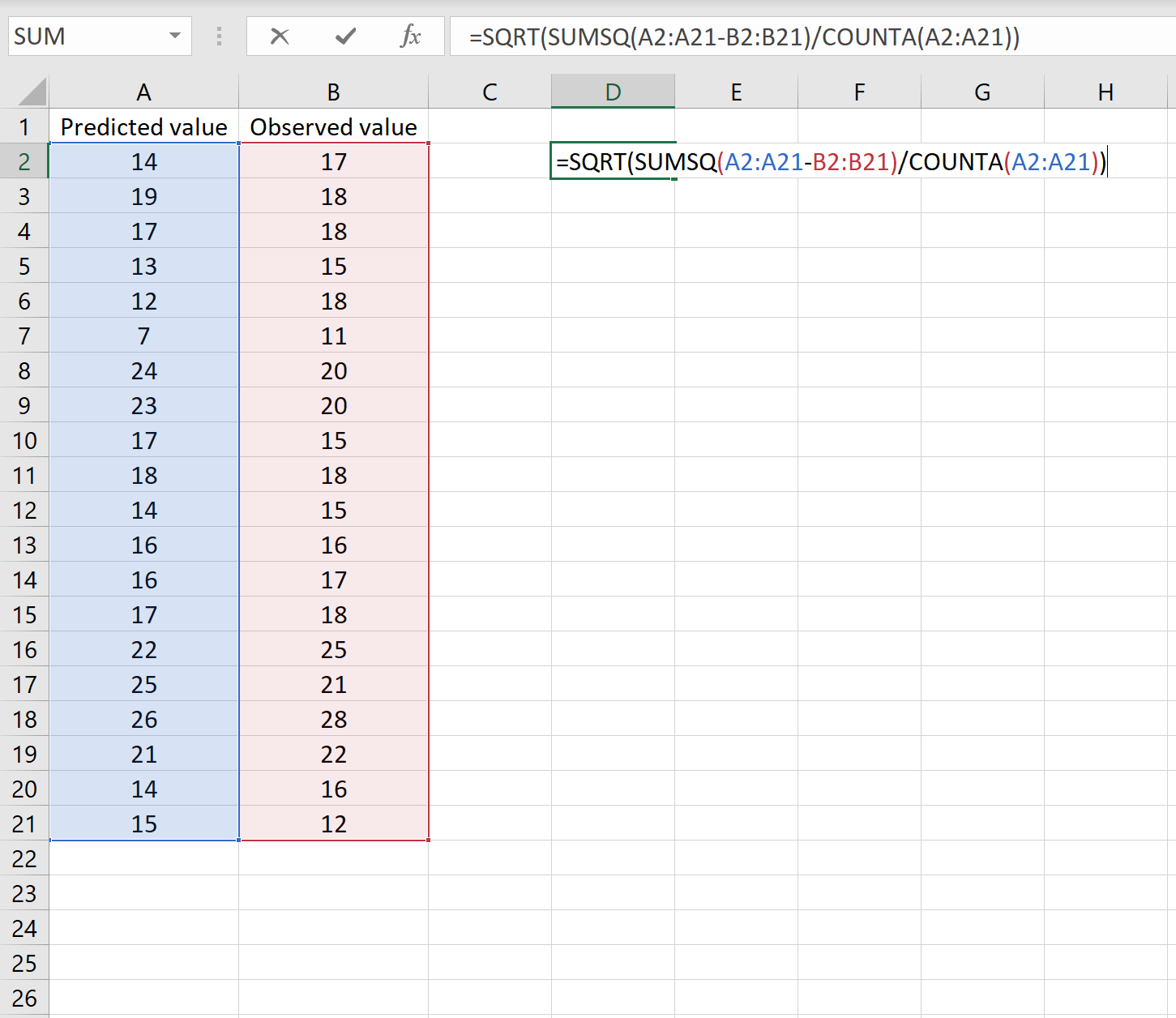
Öyleyse, aşağıdaki formülü herhangi bir hücreye yazıp CTRL+SHIFT+ENTER tuşlarına basarak RMSE’yi hesaplayabilirsiniz:

=KARE(TOPLA(A2:A21-B2:B21) / SAYIM(A2:A21))

Bu bize ortalama kare hatasının 2,6646 olduğunu söyler.

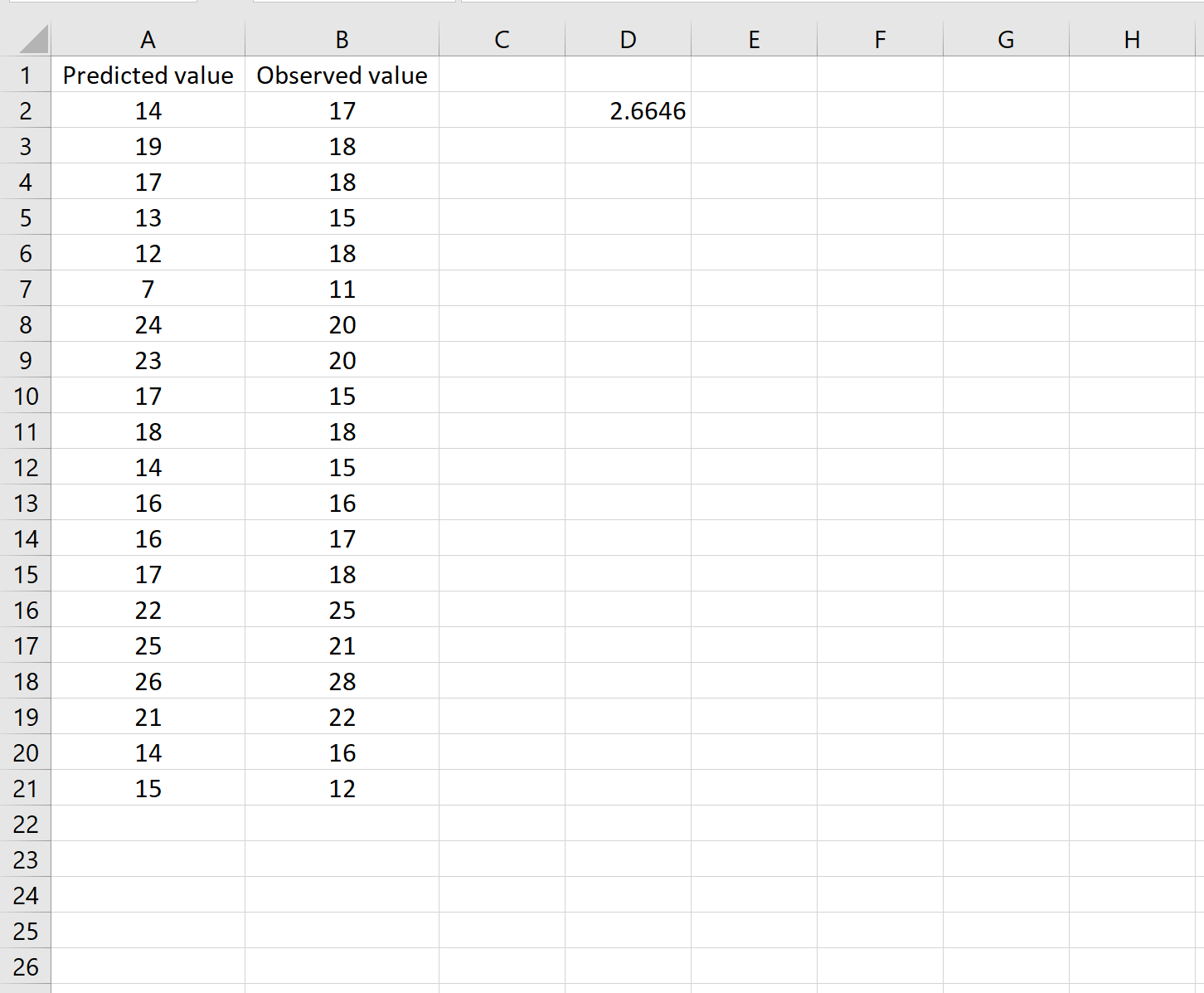
Formül biraz karmaşık görünebilir, ancak parçalara ayrıldığında anlamlıdır:

= KARE( TOPLAM(A2:A21-B2:B21) / SAYIM(A2:A21) )

• Öncelikle SUMSQ() fonksiyonunu kullanarak tahmin edilen ve gözlemlenen değerler arasındaki farkların karelerinin toplamını hesaplıyoruz.
• Daha sonra, bir aralıktaki boş olmayan hücrelerin sayısını sayan COUNTA() işlevini kullanarak veri kümesinin örnek boyutuna böleriz.
• Son olarak SQRT() fonksiyonunu kullanarak tüm hesaplamanın karekökünü alıyoruz.

Senaryo 2

Başka bir senaryoda, tahmin edilen ve gözlemlenen değerler arasındaki farkları zaten hesaplamış olabilirsiniz. Bu durumda farklılıkları gösteren yalnızca bir sütununuz olacaktır.

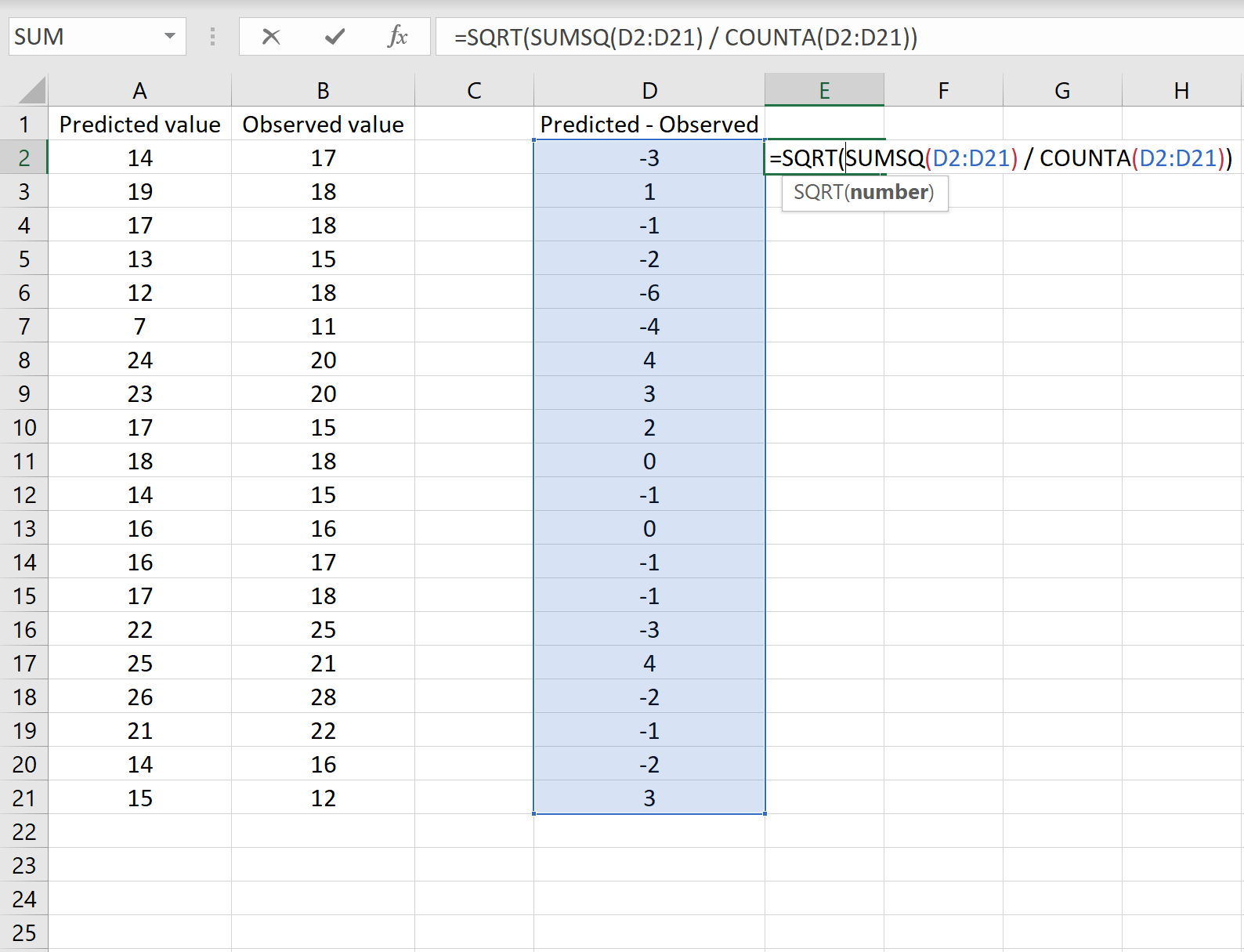
Aşağıdaki resimde bu senaryonun bir örneği gösterilmektedir. Tahmin edilen değerler A sütununda, gözlemlenen değerler B sütununda ve tahmin edilen ve gözlemlenen değerler arasındaki fark D sütununda gösterilir:

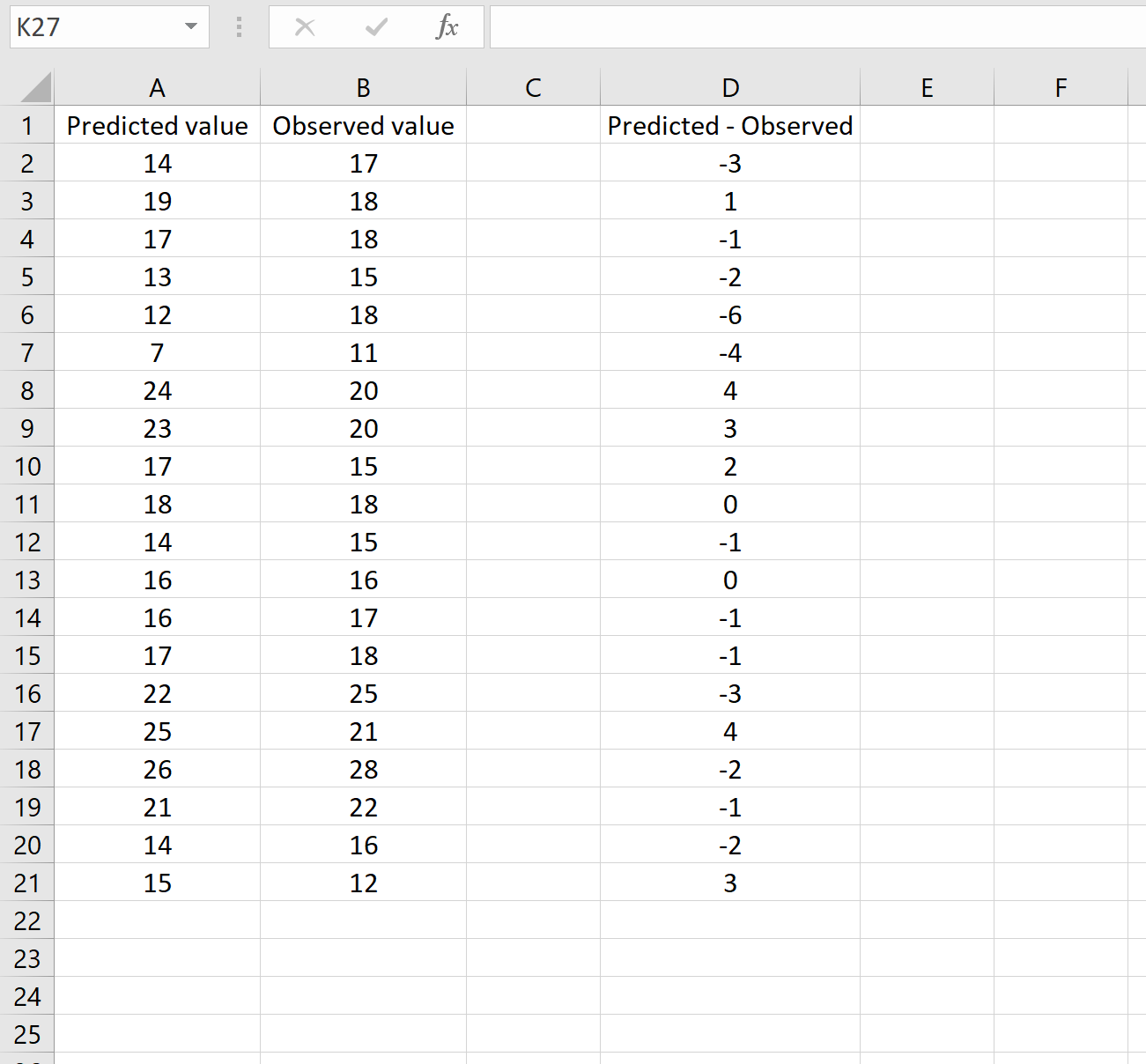
Öyleyse, aşağıdaki formülü herhangi bir hücreye yazıp CTRL+SHIFT+ENTER tuşlarına basarak RMSE’yi hesaplayabilirsiniz:

=KARE(TOPLA(D2:D21) / SAYIM(D2:D21))

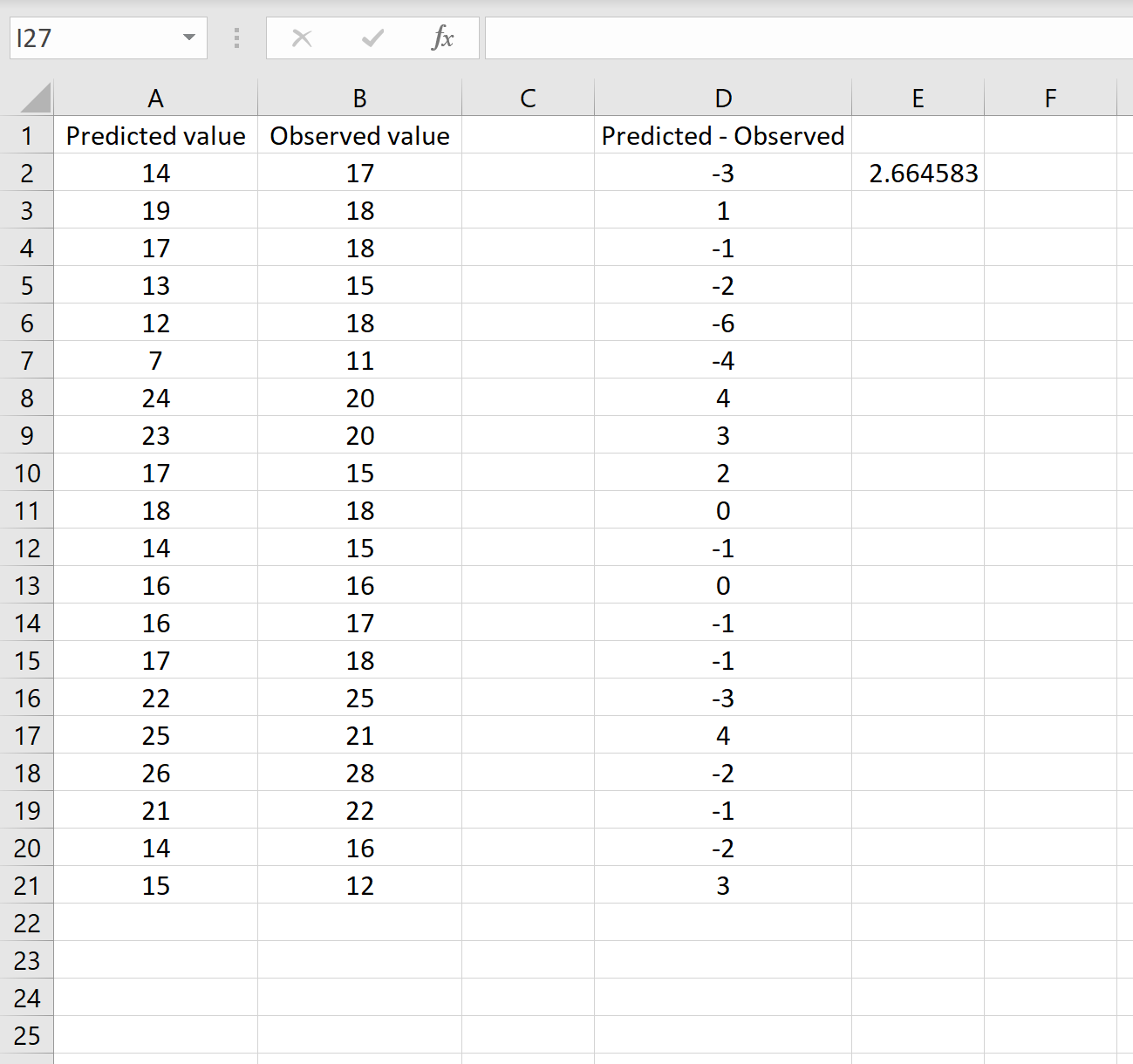
Bu bize ortalama kare hatasının 2,6646 olduğunu söyler ve bu da birinci senaryoda elde edilen sonuca karşılık gelir. Bu, RMSE’nin hesaplanmasına yönelik bu iki yaklaşımın eşdeğer olduğunu doğrulamaktadır.

Bu senaryoda kullandığımız formül, önceki senaryoda kullandığımızdan yalnızca biraz farklıdır:

= KARE( TOPLA(D2:D21) / SAYIM(D2:D21) ) )

• Tahmin edilen ve gözlemlenen değerler arasındaki farkları zaten D sütununda hesapladığımız için SUMSQ() fonksiyonunu kullanarak kareleri alınmış farkların toplamını hesaplayabiliriz .   yalnızca D sütunundaki değerlerle çalışır.
• Daha sonra, bir aralıktaki boş olmayan hücrelerin sayısını sayan COUNTA() işlevini kullanarak veri kümesinin örnek boyutuna böleriz .
• Son olarak SQRT() fonksiyonunu kullanarak tüm hesaplamanın karekökünü alıyoruz .

RMSE nasıl yorumlanır?

Daha önce de belirtildiği gibi RMSE , bir regresyon modelinin (veya tahmin edilen değerleri üreten herhangi bir modelin) bir veri kümesine ne kadar iyi “uyabildiğini” görmenin yararlı bir yoludur.

RMSE ne kadar büyük olursa, tahmin edilen ve gözlemlenen değerler arasındaki fark da o kadar büyük olur; bu da regresyon modelinin verilere uymasının o kadar kötü olduğu anlamına gelir. Tersine, RMSE ne kadar küçük olursa model verilere o kadar iyi uyum sağlayabilir.

Hangi modelin verilere en iyi şekilde uyduğunu görmek için iki farklı modelin RMSE’sini karşılaştırmak özellikle yararlı olabilir.

Excel’de daha fazla eğitim için istatistiklerle ilgili tüm Excel eğitimlerini listeleyen Excel Kılavuzları sayfamıza göz atmayı unutmayın.