Kökenden regresyon: tanım ve örnek

Basit doğrusal regresyon, bir veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanılabilen bir yöntemdir.

Basit bir doğrusal regresyon modeli aşağıdaki formu alır:

y = β ₀ + β ₁ x

Altın:

• y : Yanıt değişkeninin değeri
• β ₀ : x = 0 olduğunda yanıt değişkeninin değeri (“kesişme” terimi olarak adlandırılır)
• β ₁ : x’teki bir birimlik artışla ilişkili yanıt değişkenindeki ortalama artış
• x : Tahmin değişkeninin değeri

Bu modelin değiştirilmiş bir versiyonu, x 0’a eşit olduğunda y’yi 0’a eşit olmaya zorlayan orijin üzerinden regresyon olarak bilinir.

Bu tür bir model aşağıdaki formu alır:

y = _β1x

Kesişme teriminin modelden tamamen kaldırıldığını unutmayın.

Bu model bazen araştırmacıların, yordayıcı değişken sıfır olduğunda yanıt değişkeninin de sıfır olması gerektiğini bildiği durumlarda kullanılır.

Gerçek dünyada bu tür modeller çoğunlukla ormancılık veya ekolojik çalışmalarda kullanılır.

Örneğin araştırmacılar ağaç yüksekliğini tahmin etmek için ağaç çevresini kullanabilirler. Belirli bir ağacın çevresi sıfırsa yüksekliği de sıfır olmalıdır.

Dolayısıyla bu verilere bir regresyon modeli uydururken orijinal terimin sıfırdan farklı olmasının bir anlamı olmayacaktır.

Aşağıdaki örnek, sıradan bir basit doğrusal regresyon modelinin yerleştirilmesi ile regresyonu orijin aracılığıyla uygulayan bir modelin yerleştirilmesi arasındaki farkı göstermektedir.

Örnek: orijinden regresyon

Bir biyoloğun ağaç yüksekliğini tahmin etmek için ağaç çevresini kullanarak bir regresyon modeli uydurmak istediğini varsayalım. Dışarı çıkıyor ve 15 ağaçtan oluşan bir örnek için aşağıdaki ölçümleri topluyor:

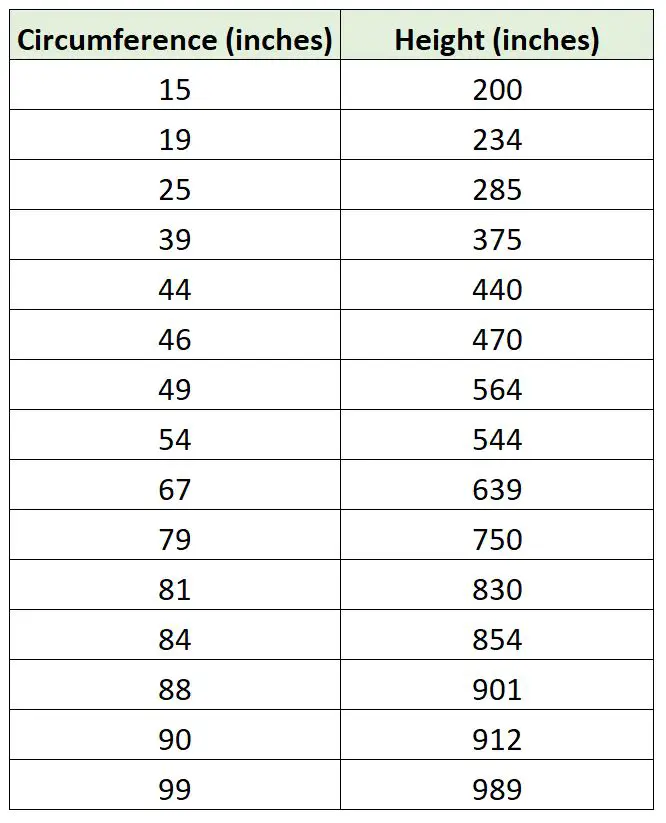
Basit bir doğrusal regresyon modelini hiçbir kesişme kullanmayan ve iki regresyon çizgisini çizen bir regresyon modeliyle eşleştirmek için R’de aşağıdaki kodu kullanabiliriz:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

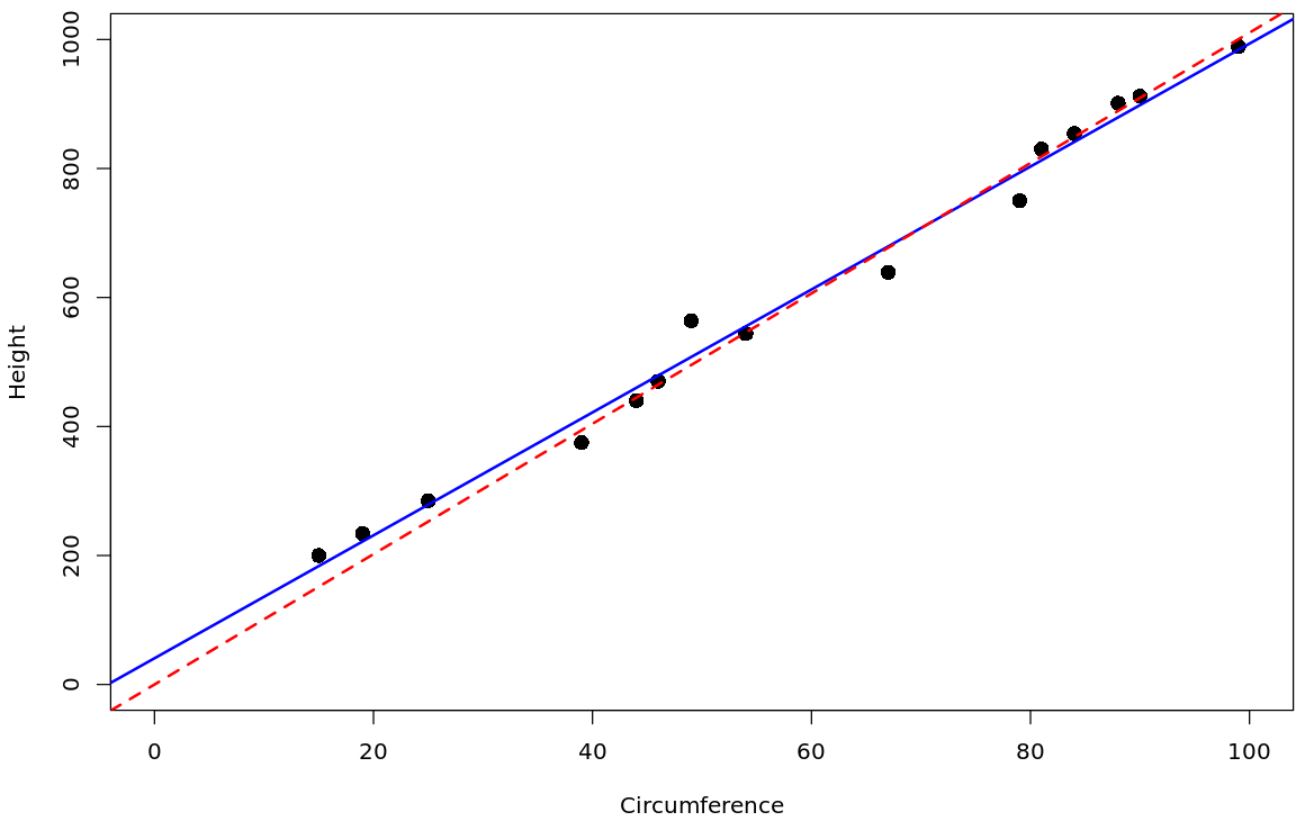
Kırmızı noktalı çizgi orijinden geçen regresyon modelini, mavi düz çizgi ise sıradan basit doğrusal regresyon modelini temsil eder.

Her model için katsayı tahminlerini elde etmek amacıyla R’de aşağıdaki kodu kullanabiliriz:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

Basit doğrusal regresyon modeli için uygun denklem şöyledir:

Yükseklik = 40,6969 + 9,5296 (çevre)

Ve orijine göre regresyon modeli için uygun denklem şu şekildedir:

Yükseklik = 10,1057 (çevre)

Çevre değişkenine ilişkin katsayı tahminlerinin biraz farklı olduğunu unutmayın.

Köken Yoluyla Regresyon Kullanımına İlişkin Önlemler

Kesişme regresyonunu kullanmadan önce, tahmin değişkeni için 0 değerinin, yanıt değişkeni için 0 değerini ima ettiğinden kesinlikle emin olmalısınız. Birçok senaryoda kesin olarak bilmek neredeyse imkansızdır.

Ve eğer orijini tahmin etmede bir miktar özgürlükten tasarruf etmek için orijin üzerinden regresyon kullanırsanız, örneklem boyutunuz yeterince büyükse, bu nadiren önemli bir fark yaratır.

Köken üzerinden regresyon kullanmayı tercih ederseniz, nihai analizinizde veya raporunuzda gerekçenizi ana hatlarıyla belirttiğinizden emin olun.

Ek kaynaklar

Aşağıdaki eğitimler doğrusal regresyon hakkında ek bilgi sağlar:

Basit Doğrusal Regresyona Giriş
Çoklu Doğrusal Regresyona Giriş
Regresyon Tablosu Nasıl Okunmalı ve Yorumlanmalı