P kontrol kartı
Bu yazıda P kontrol grafiklerinin ne olduğunu ve ne için kullanıldığını öğreneceksiniz. Ayrıca bir P kontrol grafiğinin nasıl oluşturulacağını da açıklıyoruz ve ayrıca adım adım çözülmüş bir alıştırmayı görebileceksiniz.
P kontrol şeması nedir?
P kontrol grafiği veya basitçe P grafiği , kusurlu birimlerin oranının ve bunların kontrol sınırlarının gelişimini temsil eden bir grafiktir. Bu nedenle P kontrol grafiği, kusurlu birimlerin oranını kontrol etmek için kullanılan bir grafiktir.
Kalite yönetiminde sıklıkla üretim sürecinde birimlerin doğru şekilde üretilip üretilmediğini veya tam tersine çok fazla kusurun meydana gelip gelmediğini araştırmak zorundayız. Böylece kontrol grafiği P, kusurlu birimlerin yüzdesinin gelişimini analiz etmeyi ve üretim sürecinin ne zaman kontrol altında olup olmadığını görmeyi mümkün kılar.
Bununla birlikte, P kontrol şeması yalnızca bir üretim sürecini kontrol etmek için kullanılmaz, aynı zamanda hasta oranının kontrol edilmesi veya ikili bir deneyin başarı oranının kontrol edilmesi gibi başka uygulamalara da sahiptir. Esas olarak üretim süreçlerini kontrol etmek için kullanılmasına rağmen.
P kontrol grafiğinin özelliklerinden biri, analiz edilen farklı numunelerin boyutunun mutlaka eşit olmasının gerekmemesidir, böylece istatistiksel çalışmayı gerçekleştirmek için farklı boyutlarda numuneler alınabilir.
Kısacası, P kontrol şeması iki olası sonucun olduğu durumları analiz etmemizi sağlar: “başarı” (iyi üretilmiş birim) ve “başarısızlık” (kusurlu birim). Yani, P kontrol grafiği binom dağılımını takip eden durumlar için kullanışlıdır.
P Kontrol Tablosu Nasıl Oluşturulur
Bir P kontrol grafiği oluşturmak için aşağıdaki adımları izlemelisiniz:
- Örnek al : Öncelikle grafikte oranın nasıl değiştiğini görmek için farklı örnekler almanız gerekiyor. Numuneler farklı boyutlarda olabilir ancak minimum 20 numune alınması tavsiye edilir.
- Oranı hesaplayın p : Her örnek için eksik bireylerin oranını hesaplamanız gerekir.
- Oranın ortalama değerini hesaplayın : İncelenen tüm unsurlardan kusurlu birimlerin toplam oranını hesaplamanız gerekir.
- P-grafiği kontrol limitlerini hesaplayın : Test edilen her numune için aşağıdaki formülleri kullanarak kontrol limitlerini bulmanız gerekir. Her numunenin boyutu farklıysa kontrol limitlerinin değerinin değişeceğini unutmayın.
- Değerleri grafik üzerinde çizin : Artık elde edilen numune oranlarının değerlerini ve hesaplanan kontrol limitlerini grafik üzerinde çizmeniz gerekiyor.
- P kontrol grafiğini analiz edin : son olarak geriye kalan tek şey, oranların hiçbir değerinin kontrol limitlerini aşmadığını ve dolayısıyla sürecin kontrol altında olduğunu kontrol etmektir. Aksi takdirde üretim sürecini düzeltecek önlemlerin alınması gerekir.
![]()
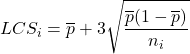
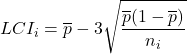
Altın
![]()
Ve
![]()
sırasıyla numune i’nin üst ve alt kontrol limitleridir,
![]()
kusur oranının ortalama değeridir ve
![]()
örneklem büyüklüğü i’dir.
P kontrol grafiği örneği
Konsepti özümsemeyi tamamlamak için, P kontrol kartı oluşturmanın çözülmüş bir örneğini göreceğiz.
- Bir şirket 25 ürün numunesi topladı ve her numuneye numunenin boyutunu ve bulunan kusurlu parça sayısını kaydetti. Toplanan verileri aşağıdaki tabloda görebilirsiniz:
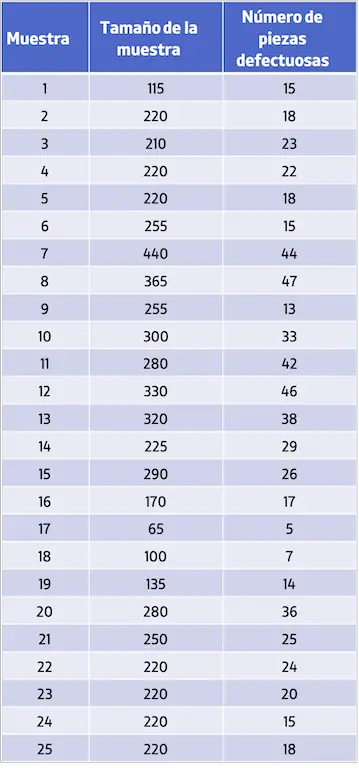
P kontrol grafiğini oluşturmak için öncelikle kusurlu birimlerin toplam oranının hesaplanması gerekir. Bunu yapmak için toplam kusur sayısını üretilen toplam birim sayısına bölmeniz yeterlidir:
![]()
Şimdi her numune için kusur oranını ve her numune için kontrol limitlerini hesaplayalım. Örnek olarak, ilk örneği hesaplamaya devam ediyoruz:
![]()
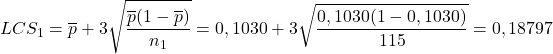
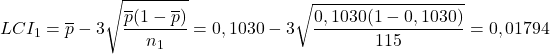
Böylece her numune için kusurların oranı ve kontrol limitleri aşağıdaki gibidir:
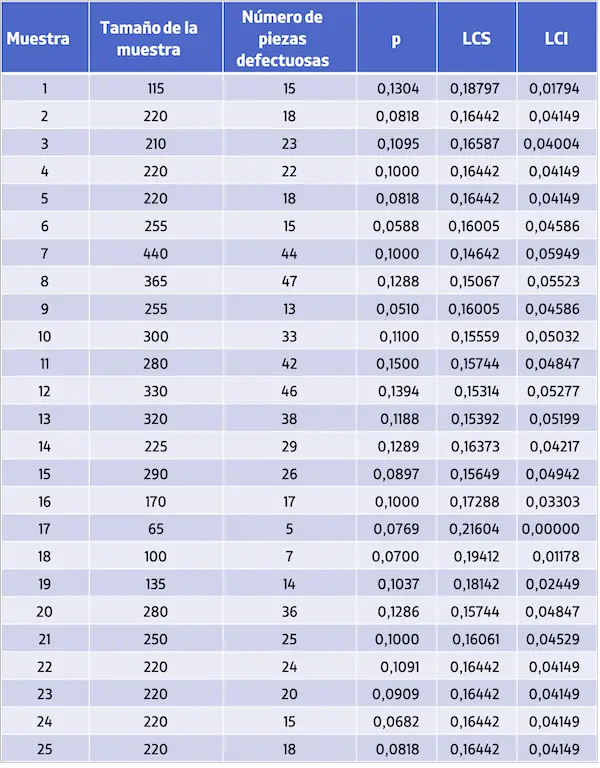
Tüm kontrol limitlerini hesapladıktan sonra, P kontrol grafiğini elde etmek için kusur oranlarının değerlerini ve bunların kontrol limitlerini bir grafik üzerinde temsil ederiz:
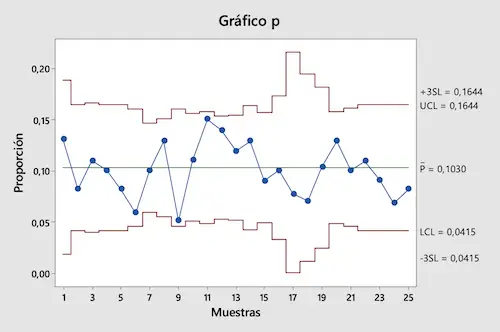
Grafikten de görebileceğiniz gibi tüm orantı değerleri kontrol sınırları içerisindedir. Bu nedenle incelenen üretim sürecinin kontrol altında olduğu sonucuna vardık.
Diğer Kontrol Tablosu Türleri
P şeması bir tür nitelik kontrol şemasıdır. Diğer mevcut özellik kontrol grafikleri şunları içerir:
- NP kontrol kartı – P kartından farklı olarak kusurlu ürünlerin oranı değil, kusurlu ürünlerin sayısı kontrol edilir.
- Kontrol kartı C : Oluşan arıza sayısı izlenir.
- Kontrol grafiği U : Kusur sayısı C tablosundaki gibi kontrol edilir, ancak örneklem büyüklüğü değişkendir.