Kontrol limitleri

İle Dr.benjamin anderson Ağustos 2, 2023 Kalite yönetimi 0 Yorum

Bu makalede, kontrol limitinin ne olduğu ve bir kontrol grafiğinin farklı kontrol limitlerinin neler olduğu açıklanmaktadır. Ayrıca kontrol limitlerinin nasıl hesaplandığını ve bir prosesin kontrol limitlerinin belirlendiği çalışılmış bir örneği de göreceksiniz.

Kontrol sınırları nedir?

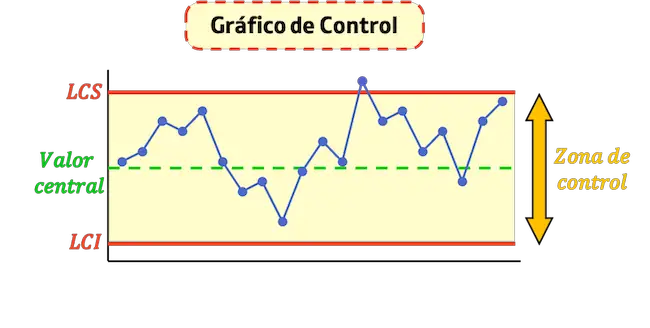
Kontrol limitleri, bir prosesin kontrol edilip edilmediğini belirlemek için kullanılan kontrol grafiğindeki yatay çizgilerdir.

Bir kontrol grafiğinin iki kontrol limiti vardır: sırasıyla kontrol alanını üstte ve altta sınırlayan üst ve alt kontrol limitleri.

Yani kontrol limitleri bir sürecin kontrol alanını belirtmek için kullanılan değerlerdir. Bir prosesten elde edilen ölçüm kontrol limitleri içerisinde ise proses kontrol ediliyor demektir. Aksi takdirde makine veya prosesin sapmış olma ihtimali olduğundan kontrol edilmesi gerekir.

Kontrol limiti türleri

Kontrol sınırları şunlardır:

Üst Kontrol Limiti (LCS) : Proseste kabul edilen maksimum değeri gösteren çizgidir.
Alt Kontrol Limiti (LCI) : Süreçte kabul edilen minimum değeri gösteren çizgidir.
Merkezi kontrol çizgisi : Grafiğin ortalama değerini temsil eden çizgidir. Noktalar bu doğruya ne kadar yakınsa süreç o kadar istikrarlı olur.

Kontrol Limitleri Nasıl Hesaplanır?

Günümüzde bir prosesin kontrol limitleri genellikle prosesin kontrol edilmesini sağlayan bilgisayar yazılımları ile hesaplanmaktadır. Ancak, bunları manuel olarak bulmanız gerekebileceğinden bunların nasıl hesaplandığını bilmeniz de önemlidir.

Bir kontrol grafiğinin kontrol limitlerinin hesaplanması, yapmak istediğiniz grafiğin türüne bağlıdır çünkü değerler, bunun ortalama veya aralık için bir kontrol grafiği olmasına bağlı olarak değişecektir.

Ortalama kontrol grafiği, bir sürecin ortalamasının gelişiminin değerlendirildiği bir grafiktir. Dolayısıyla, bir dizi değerin ortalaması aşağıdaki formül kullanılarak hesaplanır:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Altın:

$x_i$

ölçü numarası i’dir.
$n$

alınan ölçümlerin sayısıdır.

Ortalama için kontrol grafiğinin merkezi değerini şu şekilde belirleyeceğiz:

$\overline{\overline{X}}$

örneklerin ortalaması olan ve aşağıdaki ifadeyle hesaplanır:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Altın:

$\overline{X}_j$

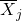
j örneğinin ortalamasıdır.
$m$

alınan numunelerin sayısıdır.

➤ Bakınız: Aritmetik ortalamanın hesaplanması

Buna karşılık, kapsam kontrol tablosunun merkezi değeri, alınan tüm numunelerin kapsamlarının ortalamasıdır:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Altın:

$R_j$

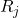
j örneğinin aralığıdır.
$m$

alınan numunelerin sayısıdır.

➤ Bakınız: İstatistiksel aralığın hesaplanması

Dolayısıyla bir kontrol grafiğinin kontrol limitlerini hesaplamaya yönelik formüller aşağıdaki gibidir:

kontrol kartı

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

R kontrol kartı

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

A ₂ , D ₃ ve D ₄ parametrelerinin değerleri aşağıdaki tabloda bulunur:

Boyut (no.)	_2’de	_3. Gün	_J4
2	1.880	0,000	3.267
3	1.023	0,000	2.575
4	0,729	0,000	2.282
5	0,577	0,000	2.115
6	0,483	0,000	2004
7	0,419	0,076	1.924
8	0,373	0,136	1.864
9	0,337	0,184	1.816
on	0,308	0,223	1.777

Kontrol limitlerinin hesaplanmasına örnek

Bir sanayi şirketi, üretim sürecinin kontrol altında olup olmadığını görmek için bir silindirin çapının ölçümünü kontrol etmek istiyor. Bunu yapmak için her 15 dakikada bir 5 silindirden numune alın ve çaplarını ölçün. Aşağıdaki tabloda ölçüm kaydı gösterilmektedir.

Kontrol limitlerini bulmak için öncelikle her ölçüm grubunun aritmetik ortalamasını ve aralığını almalıyız:

kontrol grafiği hesaplamalarına örnekler

Şimdi sırasıyla ortalama ve aralık için kontrol grafiğinin merkezi değerleri olacak ortalama ve aralıkların ortalamasını hesaplayalım:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

Bu durumda her numune 5 ölçümden oluşur, dolayısıyla kontrol limit formüllerinin katsayıları aşağıdaki gibidir:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Ortalama ve genişletilmiş kontrol grafiğinin üst ve alt kontrol limitlerini hesaplıyoruz:

Kontrol Grafiği Kontrol Limitleri

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Kontrol limitleri R kontrol kartı

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Bu nedenle egzersiz kontrol kartları aşağıdaki gibidir:

kontrol limitlerinin hesaplanması örneği

İlk kontrol grafiğinde iki değerin alt kontrol limitinden küçük olduğunu görebiliyoruz. Ayrıca ikinci kontrol grafiğinde de üst kontrol limitinin üzerinde bir değer bulunmaktadır. Bu nedenle süreç kontrol edilmez.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Kontrol sınırları nedir?

Kontrol limiti türleri

Kontrol Limitleri Nasıl Hesaplanır?

Kontrol limitlerinin hesaplanmasına örnek

yazar hakkında

Dr.benjamin anderson

Yorum ekle