Korelasyon matrisi

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede korelasyon matrisinin ne olduğunu, formülünün ne olduğunu ve korelasyon matrisinin nasıl yorumlanacağını keşfedeceksiniz. Ek olarak korelasyon matrisinin yorumlanmasına ilişkin somut bir örnek görebileceksiniz.

Korelasyon matrisi nedir?

Korelasyon matrisi, i,j konumunda i ve j değişkenleri arasındaki korelasyon katsayısını içeren bir matristir.

Dolayısıyla korelasyon matrisi, ana köşegen üzerindekilerle dolu bir kare matris olup, i satırı ve j sütununun elemanı, i değişkeni ile j değişkeni arasındaki korelasyon katsayısının değerinden oluşur.

Korelasyon matrisinin formülü bu nedenle aşağıdaki gibidir:

Altın

$r_{ij}$

değişkenler arasındaki korelasyon katsayısıdır

$i$

$j.$

Dolayısıyla bir veri setinin korelasyon matrisini bulmak için korelasyon katsayısının nasıl hesaplandığını bilmeniz önemlidir. Hatırlamıyorsanız, aşağıdaki bağlantıda bunu çevrimiçi hesap makinesiyle nasıl yapacağınızı öğreneceksiniz:

➤ Bakınız: korelasyon katsayısı hesaplayıcısı

Korelasyon katsayısının bir özelliği, değişkenlerin sırasının hesaplanmasında önemli olmamasıdır, yani korelasyon katsayısı

$r_{ij}$

eşdeğerdir

$r_{ji}.$

Bu nedenle korelasyon matrisi simetriktir.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

Bir korelasyon matrisinin anlamlı olabilmesi için istatistiksel veri setinin ikiden fazla değişkene sahip olması gerekir. Aksi takdirde tek bir korelasyon katsayısının belirlenmesi yeterli olacaktır ve korelasyon matrisi anlamlı olacaktır.

Korelasyon matrisi nasıl yapılır

Korelasyon matrisinin tanımı göz önüne alındığında, bu tür istatistiksel matrisin nasıl oluşturulduğunu görelim:

Her değişken çiftinin korelasyon katsayısını hesaplayın. Değişkenlerin sırasının sonucu değiştirmediğini, dolayısıyla her değişken çifti için yalnızca bir kez hesaplanması gerektiğini unutmayın.
Veri serisindeki değişken sayısıyla aynı boyutta bir kare matris oluşturun. Bu matris korelasyon matrisi olacaktır.
Korelasyon matrisinin ana köşegeninin her bir elemanına 1 koyun.
i , j değişkenlerinin korelasyon katsayısını i , j ve j , i konumlarına yerleştirin.
Korelasyon matrisi oluşturulduktan sonra geriye kalan tek şey değerlerinin yorumlanmasıdır.

Korelasyon matrisini çalıştırmanın yeterli olmadığını, daha sonra değerlerini yorumlayıp ne anlama geldiğini anlamanız gerektiğini unutmayın. Aşağıdaki bölümde bir korelasyon matrisinin nasıl yorumlanacağı açıklanmaktadır.

Korelasyon matrisinin yorumlanması

Korelasyon matrisini doğru bir şekilde yorumlamak için korelasyon katsayısının değerinin -1 ile +1 arasında değişebileceğini dikkate almak gerekir:

r=-1 : iki değişken mükemmel bir negatif korelasyona sahiptir, dolayısıyla tüm noktaların birbirine bağlandığı negatif eğimli bir çizgi çizebiliriz.
-1<r<0 : iki değişken arasındaki korelasyon negatiftir, yani bir değişken arttığında diğeri azalır. Değer -1’e ne kadar yakınsa değişkenler o kadar negatif ilişkilidir.
r=0 : İki değişken arasındaki korelasyon çok zayıftır, aslında aralarındaki doğrusal ilişki sıfırdır. Bu, değişkenlerin bağımsız olduğu anlamına gelmez çünkü doğrusal olmayan bir ilişkiye sahip olabilirler.
0<r<1 : İki değişken arasındaki korelasyon pozitiftir, değer +1’e ne kadar yakınsa değişkenler arasındaki ilişki o kadar güçlüdür. Bu durumda değişkenlerden biri artarken diğeri de değerini artırma eğilimindedir.
r=1 : iki değişken mükemmel pozitif korelasyona sahiptir, yani pozitif doğrusal ilişkiye sahiptirler.

Bu nedenle korelasyon matrisini yorumlamak için her bir korelasyon katsayısının yorumlanması ve farklı sonuçların karşılaştırılması gerekir.

Bu şekilde hangi değişkenlerin birbiriyle en çok ilişkili olduğunu, hangi değişkenlerin en önemli olduğunu, hangi değişkenlerin birbiriyle neredeyse hiç ilişkisi olmadığını vb. görebileceksiniz.

Korelasyon Matrisi Örneği

Korelasyon matrisinin nelerden oluştuğunu ve nasıl yorumlandığını tam olarak anlamak için bu bölümde bir korelasyon matrisi örneğini analiz edeceğiz:

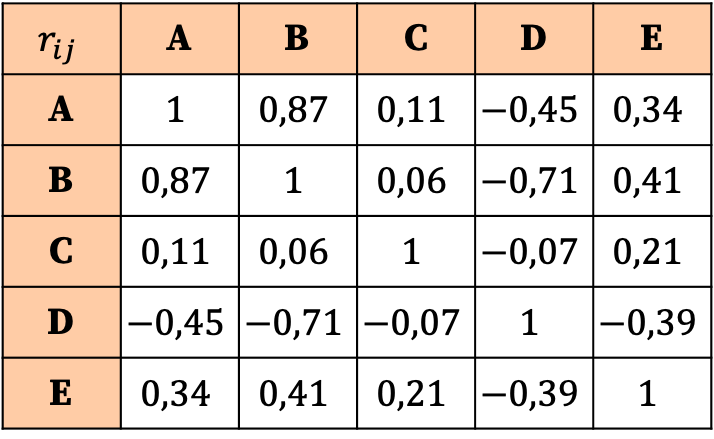
Korelasyon matrisinin yorumlanması katsayıların değerlerine dayanmaktadır. Böylece, en güçlü korelasyonun, A değişkeni ile B değişkeni arasındaki ilişki olduğunu görebiliriz, çünkü buna karşılık gelen katsayı en büyüktür (0,87).

Öte yandan, C değişkeninin neredeyse hiçbir değişkenle korelasyonu yoktur, çünkü tüm katsayıları sıfıra çok yakındır ve bu nedenle çok düşüktür. Dolayısıyla analizi basitleştirmek için bu değişkeni istatistiksel çalışmadan çıkarmayı bile düşünebiliriz.

Benzer şekilde D değişkeninin diğer değişkenlerle olan tüm ilişkileri negatiftir, yani D değişkeni ile diğer değişkenler arasındaki korelasyon terstir. Bu, değişkenin ortadan kaldırılması gerektiği anlamına gelmez, sadece D değişkeninin negatif korelasyona sahip olduğu anlamına gelir.

Gördüğünüz gibi korelasyon matrisi, verileri özetlemek ve veri kümesindeki farklı değişkenler arasındaki ilişkinin genel analizini yapmak için oldukça kullanışlıdır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil