Korelasyon matrisi nasıl okunur

İstatistikte sıklıkla iki değişken arasındaki ilişkiyi anlamaya çalışırız.

Örneğin bir öğrencinin ders çalıştığı saat ile sınavda aldığı not arasındaki ilişkiyi anlamak isteyebiliriz.

Bu ilişkiyi ölçmenin bir yolu, iki değişken arasındaki doğrusal ilişkinin bir ölçüsü olan Pearson korelasyon katsayısını kullanmaktır . -1 ile 1 arasında bir değere sahiptir; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Korelasyon katsayısı sıfırdan ne kadar uzaksa, iki değişken arasındaki ilişki o kadar güçlüdür.

İlgili: Ne “güçlü” bir korelasyon olarak kabul edilir?

Ancak bazı durumlarda birden fazla değişken çifti arasındaki korelasyonu anlamak isteriz. Bu durumlarda, çeşitli değişkenler arasındaki korelasyon katsayılarını gösteren kare bir tablo olan bir korelasyon matrisi oluşturabiliriz.

Korelasyon Matrisi Örneği

Aşağıdaki korelasyon matrisi, eğitimle ilgili çeşitli değişkenler arasındaki korelasyon katsayılarını sunmaktadır:

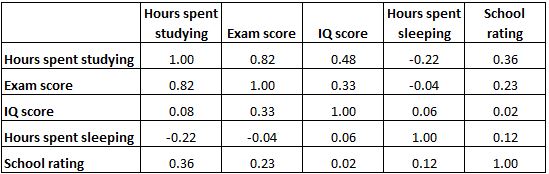
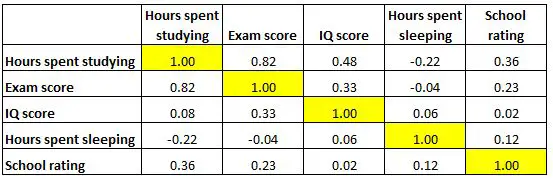
Tablodaki her hücre, iki spesifik değişken arasındaki korelasyonu gösterir. Örneğin, aşağıda vurgulanan hücre, “çalışmaya harcanan saat” ile “sınav notu” arasındaki korelasyonun 0,82 olduğunu gösterir; bu da bunların güçlü bir pozitif korelasyona sahip olduğunu gösterir. Çalışmaya harcanan daha fazla saat, daha yüksek sınav puanlarıyla yakından bağlantılıdır.

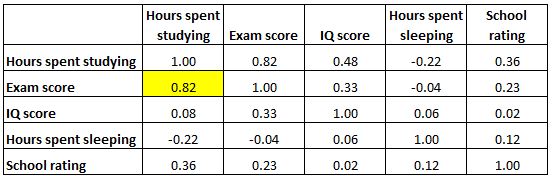
Aşağıda vurgulanan hücre, “çalışmaya harcanan saat” ile “uykuya harcanan saat” arasındaki korelasyonun -0,22 olduğunu gösteriyor, bu da bunların zayıf negatif korelasyona sahip olduğunu gösteriyor. Çalışmaya harcanan daha fazla saat, uykuya harcanan saatlerin azalmasıyla ilişkilidir.

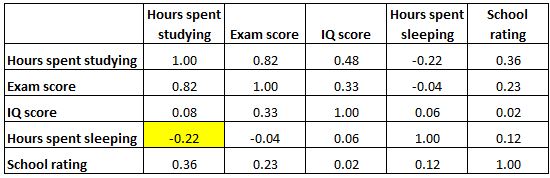
Aşağıda vurgulanan hücre, “uykuda harcanan saat” ile “IQ puanı” arasındaki korelasyonun 0,06 olduğunu gösteriyor, bu da bunların temelde korelasyonsuz olduğunu gösteriyor. Bir öğrencinin uyuduğu saat sayısı ile IQ puanı arasında çok az bir ilişki vardır.

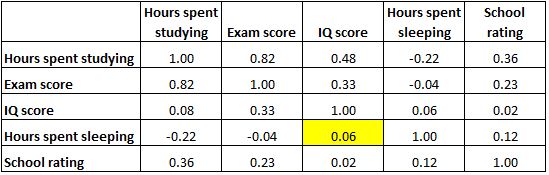
Ayrıca tablonun köşegeni boyunca korelasyon katsayılarının hepsinin 1’e eşit olduğuna dikkat edin, çünkü her değişken kendisi ile mükemmel bir korelasyona sahiptir. Bu hücreler yorumlama için kullanışlı değildir.

Korelasyon matrisinin varyasyonları

Bir korelasyon matrisinin tamamen simetrik olduğunu unutmayın. Örneğin, sağ üst hücre, sol alt hücreyle tam olarak aynı değeri gösterir:

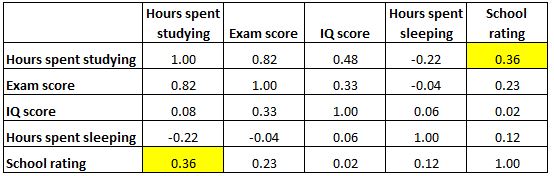
Gerçekten de iki hücre, “çalışmaya harcanan saat” ile “okul notu” arasındaki ilişkiyi ölçer.

Korelasyon matrisi simetrik olduğundan matriste görüntülenen korelasyon katsayılarının yarısı gereksiz ve gereksizdir. Yani bazen korelasyon matrisinin yalnızca yarısı görüntülenecektir:

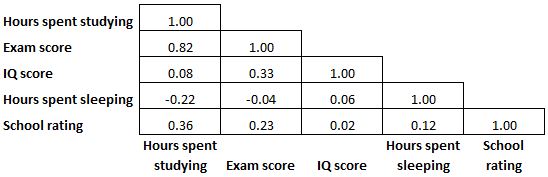
Bazen korelasyon matrisi, korelasyon katsayılarının okunmasını daha da kolaylaştırmak için ısı haritası gibi renklendirilir:

Korelasyon matrisi ne zaman kullanılır?

Uygulamada, bir korelasyon matrisi genellikle üç nedenden dolayı kullanılır:

1. Korelasyon matrisi bir dizi veriyi uygun şekilde özetler.

Korelasyon matrisi, bir veri setindeki tüm değişkenler arasındaki korelasyonları özetlemenin basit bir yoludur. Örneğin, 1000 öğrenciye ait aşağıdaki bilgileri içeren aşağıdaki veri kümesine sahip olduğumuzu varsayalım:

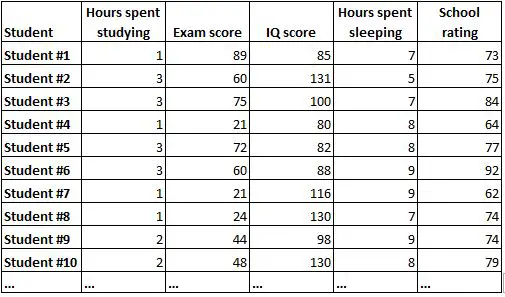
Sadece ham verilere bakarak her değişken arasındaki ilişkiyi anlamak çok zor olacaktır. Neyse ki bir korelasyon matrisi, her değişken çifti arasındaki korelasyonu hızlı bir şekilde anlamamıza yardımcı olabilir.

2. Korelasyon matrisi regresyonun tanısına hizmet eder.

Çoklu doğrusal regresyonun temel varsayımlarından biri, modeldeki hiçbir bağımsız değişkenin, modeldeki diğer herhangi bir değişkenle güçlü bir korelasyona sahip olmamasıdır.

İki bağımsız değişkenin yüksek korelasyona sahip olması çoklu doğrusallık adı verilen bir problemle sonuçlanır ve regresyon sonuçlarının yorumlanmasını zorlaştırabilir.

Potansiyel bir çoklu bağlantı sorununu tespit etmenin en basit yollarından biri, bir korelasyon matrisine bakmak ve değişkenlerden herhangi birinin birbiriyle yüksek düzeyde korelasyona sahip olup olmadığını görsel olarak kontrol etmektir.

3. Korelasyon matrisi diğer analizlere girdi olarak kullanılabilir.

Açımlayıcı faktör analizi ve yapısal eşitlik modelleri gibi diğer karmaşık analizler için girdi olarak bir korelasyon matrisi kullanılır.

Ek kaynaklar

Aşağıdaki eğitimlerde çeşitli istatistiksel yazılımlar kullanılarak bir korelasyon matrisinin nasıl oluşturulacağı açıklanmaktadır:

Excel’de Korelasyon Matrisi Nasıl Oluşturulur
SPSS’de Korelasyon Matrisi Nasıl Oluşturulur
Stata’da korelasyon matrisi nasıl oluşturulur
Python’da Korelasyon Matrisi Nasıl Oluşturulur