Korelasyonu ne zaman kullanmalısınız? (açıklama ve örnekler)

Korelasyon, iki değişken arasındaki doğrusal ilişkiyi ölçmek için kullanılır.

Korelasyon katsayısı her zaman -1 ile 1 arasında bir değer alır; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Öğrencilerin sıklıkla sorduğu soru şudur: Korelasyonu ne zaman kullanmalıyım?

Kısa cevap: İki değişken arasındaki doğrusal ilişkiyi ölçmek istediğinizde ve değişkenlerin hiçbiri bir yanıt veya “sonuç” değişkenini temsil etmediğinde korelasyonu kullanın .

Aşağıdaki örnekler pratikte korelasyonu ne zaman kullanmanız gerektiğini ve kullanmamanız gerektiğini göstermektedir.

Örnek 1: Korelasyon ne zaman kullanılmalı?

Bir profesörün sınıfındaki öğrencilerinin matematik sınavı puanları ile fen bilimleri sınavı puanları arasındaki doğrusal ilişkiyi anlamak istediğini varsayalım.

Örneğin matematik sınavında iyi performans gösteren öğrenciler fen sınavında da başarılı oluyor mu? Yoksa matematikte yüksek puan alan öğrenciler fen alanında da düşük puan alma eğiliminde midir?

Bu senaryoda, matematik sınavı puanları ile fen bilimleri sınavı puanları arasındaki korelasyonu hesaplayabilir çünkü sadece iki değişken arasındaki doğrusal ilişkiyi anlamak ister ve her iki değişken de bir yanıt değişkeni olarak kabul edilemez.

Pearson korelasyon katsayısını hesapladığını ve bunun r = 0,78 olduğunu bulduğunu varsayalım. Bu güçlü bir pozitif korelasyondur, yani matematikte iyi performans gösteren öğrencilerin fen bilimlerinde de iyi performans gösterme eğiliminde olduğu anlamına gelir.

Örnek 2: Korelasyon ne zaman kullanılmamalıdır?

Diyelim ki bir şirketin pazarlama departmanı, reklam harcamalarının toplam gelir üzerindeki etkisini ölçmek istiyor.

Örneğin, reklama harcanan her ek dolar için şirket ne kadar ek gelir elde etmeyi bekleyebilir?

Bu senaryoda, “gelir” değişkeni yanıt değişkeni olduğundan, departmanın reklam harcamaları ile toplam gelir arasındaki ilişkiyi ölçmek için doğrusal bir regresyon modeli kullanması gerekir.

Departmanın basit bir doğrusal regresyon modeli uyguladığını ve aşağıdaki denklemin reklam harcamaları ile toplam gelir arasındaki ilişkiyi en iyi şekilde tanımladığını bulduğunu varsayalım:

Toplam gelir = 145,4 + 0,34*(reklam giderleri)

Bunu, reklamlara harcanan her ek doların toplam gelirde ortalama 0,34 dolar artışa yol açtığı şeklinde yorumlayabiliriz.

Korelasyonu Kullanmaya İlişkin Önlemler

Korelasyonun yalnızca iki değişken arasındaki doğrusal ilişkiyi ölçmek için kullanılabileceğini unutmamak önemlidir.

Ancak bazı durumlarda korelasyon katsayısı, doğrusal olmayan bir ilişkiyi paylaşan iki değişken arasındaki ilişkiyi etkili bir şekilde yakalayamayacaktır.

Örneğin, iki değişken arasındaki ilişkiyi görselleştirmek için aşağıdaki dağılım grafiğini oluşturduğumuzu varsayalım:

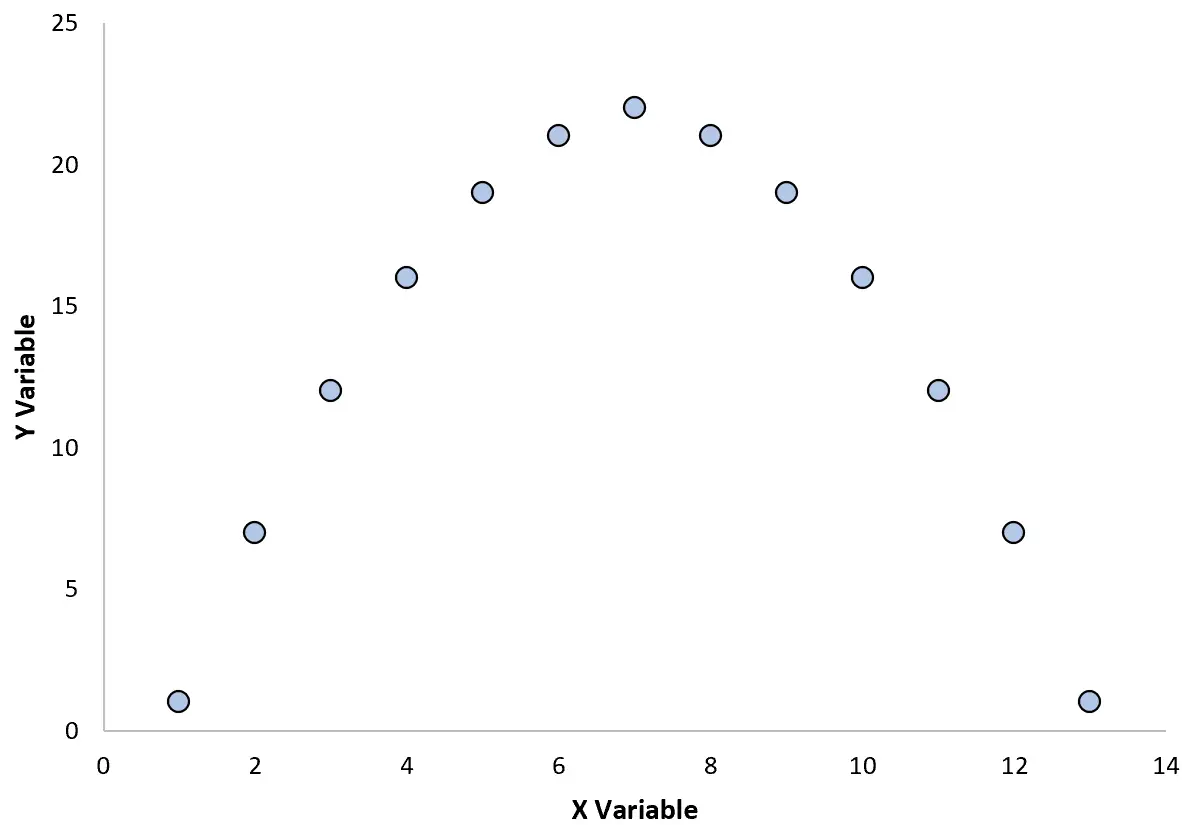
Bu iki değişken arasındaki korelasyon katsayısını hesaplarsak r=0 çıkar. Bu da iki değişken arasında doğrusal bir ilişkinin olmadığı anlamına gelir.

Ancak grafikten iki değişkenin gerçekten de bir ilişkisi olduğunu görebiliriz; bu doğrusal bir ilişki yerine sadece ikinci dereceden bir ilişkidir.

Bu nedenle, iki değişken arasındaki korelasyonu hesaplarken, değişkenler arasındaki ilişkiyi görselleştirmek için bir dağılım grafiği oluşturmanın da yararlı olabileceğini unutmayın.

İki değişkenin doğrusal bir ilişkisi olmasa bile, dağılım grafiğinde ortaya çıkacak doğrusal olmayan bir ilişkiye sahip olmaları mümkündür.

Ek kaynaklar

Aşağıdaki eğitimlerde korelasyonun farklı durumlarda nasıl kullanıldığı daha ayrıntılı olarak açıklanmaktadır:

6 gerçek hayattan korelasyon örneği
“Güçlü” bir korelasyon olarak kabul edilen şey nedir?
Korelasyon vs. dernek: fark nedir?
Korelasyon ve regresyon: fark nedir?