Koşullu olasılık (veya koşullu olasılık)

İle Dr.benjamin anderson Ağustos 6, 2023 Olasılık 0 Yorum

Burada koşullu olasılığın (veya koşullu olasılığın) ne olduğunu öğreneceksiniz. Koşullu olasılığın nasıl hesaplandığını ve bu olasılık türünün özelliklerini bir örnekle açıklıyoruz. Ayrıca adım adım çözülen koşullu olasılık alıştırmaları ile pratik yapabileceksiniz.

Koşullu olasılık nedir?

Koşullu olasılık , aynı zamanda koşullu olasılık olarak da adlandırılır, başka bir B olayının meydana gelmesi durumunda A olayının meydana gelme olasılığını gösteren istatistiksel bir ölçüdür. Yani koşullu olasılık P(A|B), A olayının B olayı gerçekleştikten sonra meydana gelme olasılığını ifade eder.

Koşullu olasılık, iki olay arasında dikey bir çubukla yazılır: P(A|B) ve şunu okur: “B olayı verildiğinde A olayının koşullu olasılığı”.

Koşullu olasılık değerinin 0 ile 1 arasında bir sayı olduğuna dikkat edin. Koşullu olasılık ne kadar yüksek olursa, B olayı meydana geldiğinde A olayının meydana gelme olasılığı da o kadar yüksek olur, ancak koşullu olasılık ne kadar düşük olursa, A olayının gerçekleşme olasılığı da o kadar düşük olur. B olayı gerçekleştiğinde gerçekleşecektir.

Koşullu Olasılık Formülü

Belirli bir B olayının A olayının koşullu olasılığı, A olayı ile B olayı arasındaki kesişme olasılığının B olayının olasılığına bölünmesine eşittir.

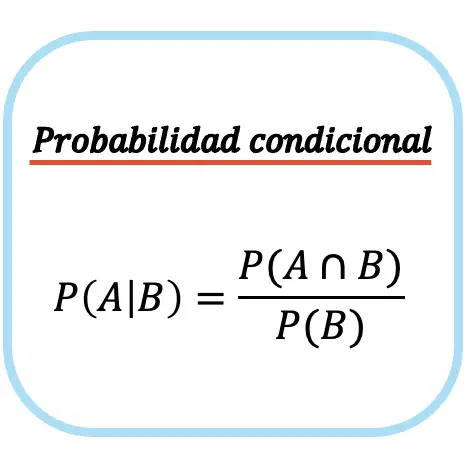
Koşullu olasılık (veya koşullu olasılık) formülünün yalnızca koşulsuz olayın meydana gelme olasılığı sıfır değilse, yani P(B)≠0 ise kullanılabileceğini unutmayın. Veya başka bir deyişle B olayının gerçekleşmesi mümkün ise.

Koşullu olasılık bunun tersinden de hesaplanabilir, yani P(B|A) biliniyorsa P(A|B) belirlenebilir. Ancak bunu yapmak için Bayes teoremini uygulamanız gerekir; bu teoremin nelerden oluştuğunu burada görebilirsiniz:

➤ Bakınız: Bayes teoremi nedir?

Koşullu Olasılık Örneği

Koşullu olasılığın tanımı ve formülünün ne olduğunu gördükten sonra, anlamını tam olarak anlamak için bu tür olasılıkların bir örneğini adım adım çözeceğiz.

30 kişilik bir sınıfta sınava girdikten sonra kaç öğrencinin okuduğunu ve kaçının geçtiğini öğrenmek için veriler toplandı. Sonuçlar aşağıdaki beklenmedik durum tablosunda sunulmaktadır. Toplanan verilerden, daha önce çalışmışsanız, sınavı geçmenin koşullu olasılığını hesaplayın.

Koşullu olasılığı elde etmek için daha önce gördüğümüz formülü uygulamalıyız:

$P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}$

Bu nedenle öncelikle bir öğrencinin okuyup çalışıp geçme olasılığını bulmamız gerekiyor. Bir öğrencinin çalışma olasılığını bulmak için Laplace kuralını kullanmamız yeterlidir, yani çalışan öğrenci sayısını toplam gözlem sayısına bölmemiz gerekir:

$P(\text{estudiado})=\cfrac{23}{30}=0,77$

Ve bir öğrencinin aynı anda çalışıp geçme olasılığını, çalışıp geçen öğrenci sayısını toplama bölerek olasılık tablosundan bulabiliriz:

$P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63$

Buna göre, bir öğrencinin çalışmış olması durumunda sınavı geçme olasılığı:

$\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}$

Bağımlı ve bağımsız olayların koşullu olasılığı

Bu bölümde koşullu olasılık ile bağımlı ve bağımsız olaylar (veya bağımlı ve bağımsız olaylar) arasındaki ilişkinin ne olduğunu göreceğiz. Çünkü her ne kadar farklı kavramlar olsa da bu iki olay türü koşullu bir olasılığa bağlıdır.

İki olay (veya oluşum), gerçekleşme olasılıkları birbirine bağlı olmadığında bağımsızdır. Böyle bir durumda iki olayın kesişimi, her bir olayın ayrı ayrı olasılığının çarpımına eşdeğerdir. Ve bu nedenle koşullu olasılık formülü basitleştirilmiştir:

$P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)$

Kısacası, eğer A ve B olayları bağımsızsa, belirli bir B olayı için A olayının koşullu olasılığı, A olayının meydana gelme olasılığına tam olarak eşittir.

Öte yandan, iki olayın birbirine bağlı olması, bir olayın olasılığının diğer olayın olasılığına bağlı olduğu anlamına gelir. Bu nedenle, iki A ve B olayı bağımlı olduğunda, belirli bir B olayı için A olayının koşullu olasılığı, A olayının meydana gelme olasılığından farklıdır.

$P(A|B)\neq P(A)$

Çözülmüş koşullu olasılık egzersizleri

1. Egzersiz

Toplarla dolu bir torbanın yarısının turuncu, diğer yarısının ise yeşil olduğunu biliyoruz. Ayrıca topların üçte biri turuncu renktedir ve aynı zamanda bir işaretle işaretlenmiştir. Turuncu bir top çektiğinizde sinyali alma olasılığı nedir?

Çözümü görün

Alıştırmayı çözmek için koşullu olasılık formülünü uygulamalıyız:

$P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}$

Sorun ifadesi bize torbanın yarısının portakal olduğunu söylüyor. Bu nedenle turuncu bir topun alınmasının teorik olasılığı %50’dir.

$P(\text{naranja})=\cfrac{1}{2}=0,5$

Öte yandan, toplamın üçte birinin turuncu top olduğunu ve sinyale sahip olduğunu biliyoruz, dolayısıyla sinyalli turuncu bir top elde etme olasılığı:

$P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33$

Son olarak, değerini bulmak için hesaplanan olasılıkları koşullu olasılık formülünde yerine koyarız:

$\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}$

Özetle, turuncu ise sinyalli bir topun çekilme olasılığı %66’dır.

Alıştırma 2

Bir kutuda altı mavi kalem ve üç siyah kalem varsa, tek bir mavi kalem çekme olasılığını ve art arda iki mavi kalem çekme olasılığını hesaplayın.

Çözümü görün

Mavi kalemi bir kez elinize alma olasılığını belirlemek için Laplace yasasını kullanmanız yeterlidir:

$P(\text{azul})=\cfrac{6}{6+3}=0,67$

Problem ayrıca bizden art arda iki mavi kalem alma olasılığını, yani daha önce mavi bir kalem almışsak mavi kalem almanın koşullu olasılığını bilmemizi istiyor.

Mavi kalem çekersek daha az avantajlı bir durumla karşı karşıya kalırız ama toplamda bir kalem daha eksik olur. Bu nedenle koşullu olasılık:

$P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63$

Alıştırma 3

Yazı-tura atıldığında tura gelmesi koşuluyla zarın 4 rakamına gelme koşullu olasılığı nedir?

Çözümü görün

Bu alıştırmayı çözmek için koşullu olasılık teorisini hesaba katmalısınız çünkü “zar atarak 4 sayısını elde etme” ve “para atarak tura gelme” olayları bağımsızdır. Bu nedenle koşullu olasılık formülünü kullanmak gerekli değildir ancak aşağıdaki eşitlik sağlanır:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})$

Dolayısıyla koşullu olasılığı bulmak için Laplace kuralını kullanmanız yeterlidir:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167$

Alıştırma 4

Bir ülkedeki 25 şirketin mali yılı incelendi ve hisse senedi fiyatlarının o yılın ekonomik sonuçlarına göre nasıl değiştiği incelendi. Toplanan verileri aşağıdaki acil durum tablosunda görebilirsiniz:

Bir şirketin geçen yıl kar elde etmesi durumunda hisse senedi fiyatının artma olasılığı nedir?

Çözümü görün

Alıştırma bize, şirketin olumlu bir ekonomik sonuç elde etmesi durumunda hisse senetlerinin artacağı koşullu olasılığını soruyor. Dolayısıyla bu olasılığı hesaplamak için koşullu olasılık formülünü kullanmalıyız:

$P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}$

Bu nedenle öncelikle bir şirketin kâr etme olasılığını, ikinci olarak da bir şirketin hisse başına fiyatını artırırken ekonomik kâr elde etme olasılığını hesaplıyoruz:

$P(\text{beneficio})=\cfrac{14}{25}=0,56$

$P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4$

Daha sonra bulunan değerleri formülde yerine koyarız ve koşullu olasılığı hesaplarız:

$\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}$

Koşullu olasılığın özellikleri

Koşullu olasılığın veya koşullu olasılığın özellikleri aşağıdaki gibidir:

A olayının belirli bir B olayının koşullu olasılığı artı tamamlayıcı A olayının belirli bir B olayının koşullu olasılığının toplamı bire eşittir.

$P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1$

A olayı B olayının bir alt kümesi ise, B doğru olduğunda A her zaman meydana gelecektir. Dolayısıyla bu durumlarda B olayı verildiğinde A olayının koşullu olasılığı 1’dir.

$B\subseteq A \ \longrightarrow \ P(A|B)=1$

İki farklı olay göz önüne alındığında, koşullu olasılığa göre aşağıdaki eşitlik her zaman geçerlidir:

$P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Koşullu olasılık nedir?

Koşullu Olasılık Formülü

Koşullu Olasılık Örneği

Bağımlı ve bağımsız olayların koşullu olasılığı

Çözülmüş koşullu olasılık egzersizleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Koşullu olasılığın özellikleri

yazar hakkında

Dr.benjamin anderson

Yorum ekle