Kovaryans matrisi

Bu makalede kovaryans matrisinin ne olduğu ve formülünün ne olduğu açıklanmaktadır. Somut bir örnekle kovaryans matrisinin nasıl oluşturulacağını ve kovaryans matrislerinin özelliklerini keşfedeceksiniz.

Kovaryans matrisi nedir?

Kovaryans matrisi, elemanları incelenen değişkenlerin varyansları ve kovaryansları olan bir kare matristir. Böylece kovaryans matrisinin ana köşegeninin elemanları her bir değişkenin varyansını, geri kalan elemanlar ise değişkenler arasındaki kovaryansları oluşturur.

İstatistikte kovaryans matrisi, iki veya daha fazla rastgele değişken arasındaki ilişkiyi analiz etmek için kullanılır. Kovaryans matrisi çok kullanışlıdır çünkü değişkenlerin tüm kovaryanslarının değerlerini aynı anda görebildiğiniz için birçok değişken arasındaki korelasyonu hızlı bir şekilde yorumlamanıza olanak tanır.

Kovaryans matrisinin sembolü, büyük Yunan harfi sigma’dır (Σ).

Kovaryans matrisi nasıl hesaplanır

Çeşitli istatistiksel değişkenlerin kovaryans matrisini hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

1. Tüm değişkenlerin varyanslarını hesaplayın.
2. Her değişken çiftinin kovaryansını hesaplayın.
3. Kovaryans matrisini oluşturun:
• i değişkeninin varyansı matrisin ana köşegenine, daha doğrusu i,i konumuna yerleştirilmelidir.
• i ve j değişkenleri arasındaki kovaryans matrisin i,j konumuna yerleştirilmelidir.

Dolayısıyla kovaryans matrisinin formülü aşağıdaki gibidir:

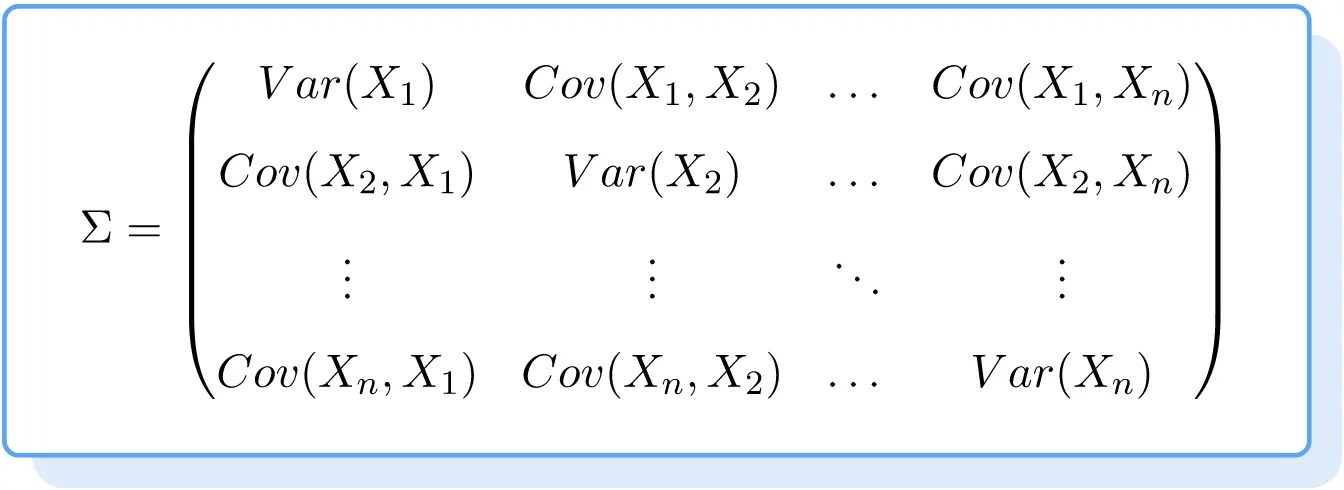
Kovaryans Matrisi Örneği

Kovaryans matrisinin tanımını gördükten sonra aşağıda adım adım bir alıştırma bulacaksınız, böylece bu tür matrislerin nasıl yapıldığını görebilirsiniz.

Değerleri aşağıdaki gibi olan X, Y ve Z değişkenlerinin kovaryans matrisini hesaplar:

• X: 4, 7, 12, 5, 7
• Ve: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

Yapmamız gereken ilk şey tüm değişkenlerin varyanslarını belirlemektir:

İkinci olarak, her bir değişken çifti arasındaki kovaryansı buluyoruz:

Ve tüm varyansları ve kovaryansları hesapladıktan sonra geriye kalan tek şey kovaryans matrisini oluşturmaktır. Bunu yapmak için varyans değerlerini matrisin ana köşegenine ve kovaryans değerlerini karşılık gelen konumlarına yerleştiririz:

Gördüğünüz gibi varyansları ve kovaryansları bir matriste temsil ederek değişkenleri yorumlamak çok kolaydır. En büyük dağılıma sahip değişken Y’dir (23.44), diğer taraftan X ve Y değişkenleri arasında doğrudan ilişki bulunurken, X ve Z (dolayısıyla Y ve Z) değişkenleri arasında ters ilişki bulunmaktadır.

İki değişken arasındaki kovaryans değişkenlerin sırasına bağlı olmadığından kovaryans matrisinin her zaman simetrik olduğunu unutmayın. Örneğin,

eşittir

Ayrıca kovaryans matrisi her zaman kare bir matris olacak ve boyutu değişken sayısına eşit olacaktır. Bu durumda üç değişkenimiz vardı ve bu yüzden bu 3×3’lük bir matris, ancak yalnızca iki değişkenimiz olsaydı kovaryans matrisi 2×2 olurdu.

Kovaryans matrisinin özellikleri

Kovaryans matrisi aşağıdaki özelliklere sahiptir:

• Kovaryans matrisi, değişken sayısı mertebesinde bir kare matristir.
• Kovaryans matrisi simetriktir, yani matrisin ana köşegeni bir simetri eksenidir.
• Kovaryans matrisi her zaman pozitif yarı tanımlıdır.
• Kovaryans matrisinin determinantı sıfıra eşit veya sıfırdan büyüktür.