Google e-tablolarda kovaryans matrisi nasıl oluşturulur

Kovaryans , bir değişkendeki değişikliklerin ikinci bir değişkendeki değişikliklerle nasıl ilişkilendirildiğinin bir ölçüsüdür. Daha spesifik olarak, iki değişkenin doğrusal olarak ilişkili olma derecesinin bir ölçüsüdür.

İki değişken ( X ve Y) arasındaki kovaryansı hesaplamak için kullanılan formül:

COV( X , Y ) = Σ(x- x )(y- y ) / n

Kovaryans matrisi, birçok farklı değişken arasındaki kovaryansı gösteren bir kare matristir. Bu, bir veri kümesinde farklı değişkenlerin nasıl ilişkili olduğunu anlamanın yararlı bir yolu olabilir.

Aşağıdaki örnek, belirli bir veri kümesi için Google E-Tablolar’da kovaryans matrisinin nasıl oluşturulacağını gösterir.

Google E-Tablolarda Kovaryans Matrisi Nasıl Oluşturulur

Diyelim ki 10 farklı öğrencinin üç dersteki (matematik, fen bilimleri ve tarih) test puanlarını gösteren aşağıdaki veri setine sahibiz.

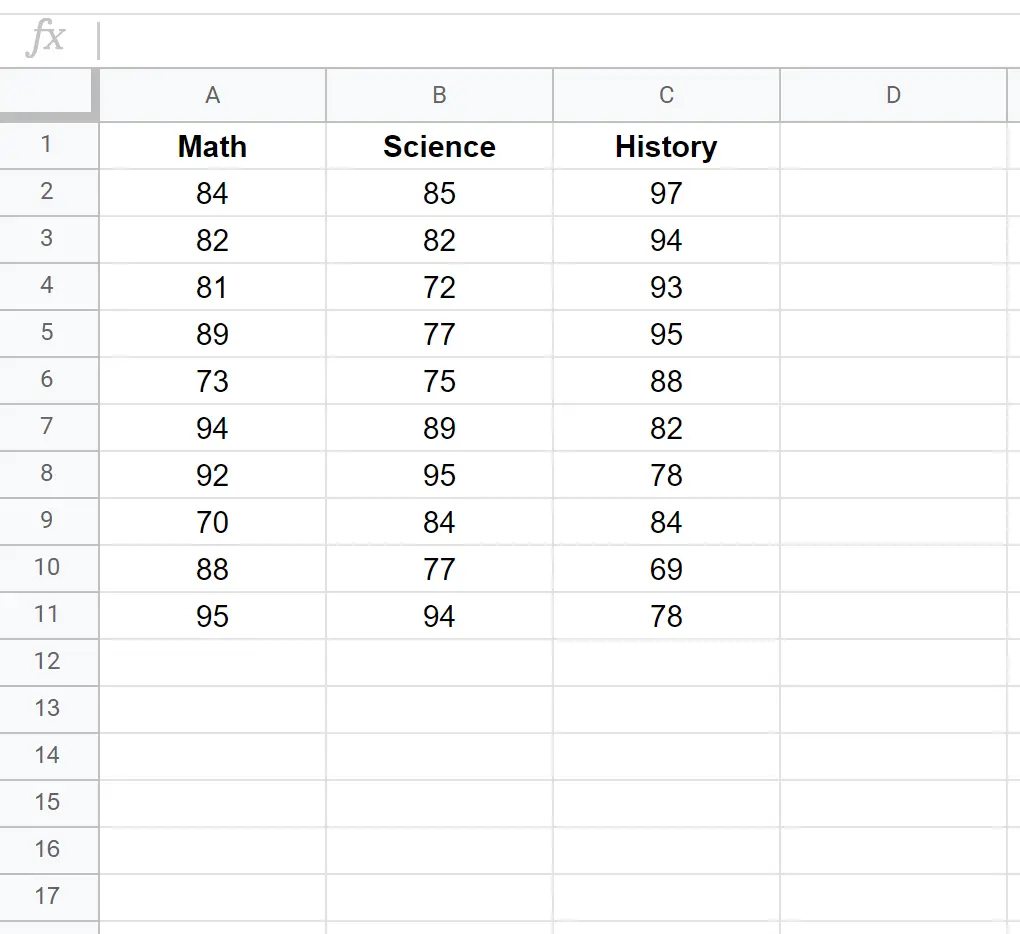
Bu veri kümesi için bir kovaryans matrisi oluşturmak amacıyla COVAR() işlevini aşağıdaki sözdizimiyle kullanabiliriz:

COVAR(veri_y; veri_x)

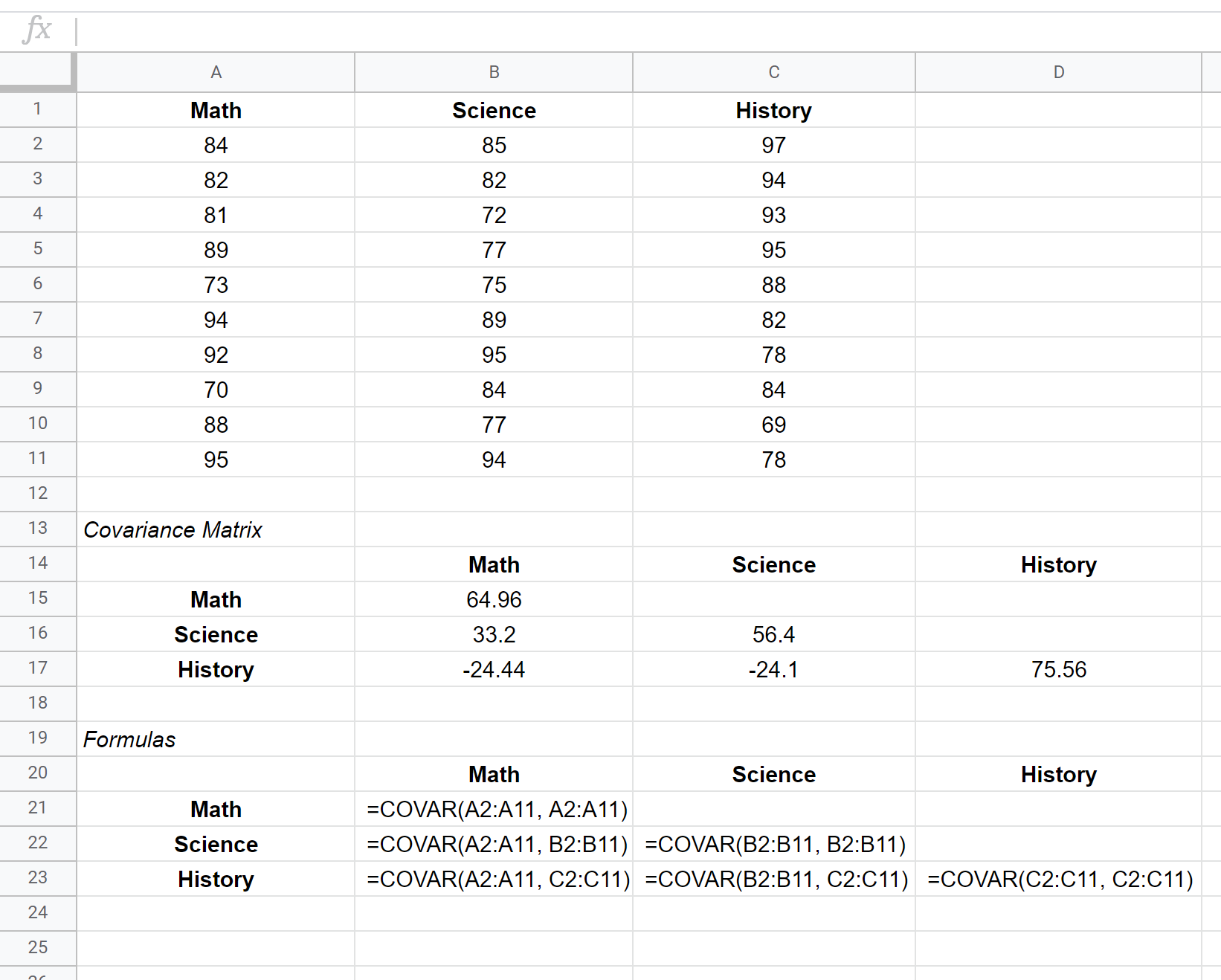
Bu veri kümesinin kovaryans matrisi B15:D17 hücrelerinde gösterilirken, kovaryans matrisini oluşturmak için kullanılan formüller aşağıdaki B21:D23 hücrelerinde gösterilmektedir:

Kovaryans matrisi nasıl yorumlanır?

Bir kovaryans matrisimiz olduğunda matris değerlerini yorumlamak kolaydır.

Matrisin köşegenleri boyunca yer alan değerler, her bir konunun basitçe varyanslarıdır. Örneğin:

• Matematik puanlarının varyansı 64,96
• Fen puanlarının varyansı 56,4
• Geçmiş puan farkı 75,56

Matrisin diğer değerleri farklı konular arasındaki kovaryansları temsil eder. Örneğin:

• Matematik ve fen bilimleri puanları arasındaki kovaryans 33,2’dir.
• Matematik ve tarih puanları arasındaki kovaryans -24,44’tür.
• Fen ve tarih puanları arasındaki kovaryans -24,1’dir.

Kovaryans için pozitif bir sayı, iki değişkenin art arda artma veya azalma eğiliminde olduğunu gösterir. Örneğin matematik ve fen bilimleri arasında pozitif bir kovaryans (33.2) vardır; bu da matematikte yüksek puan alan öğrencilerin fen bilimlerinde de yüksek puan alma eğiliminde olduğunu gösterir. Benzer şekilde matematikte zayıf performans gösteren öğrenciler fen alanında da düşük performans gösterme eğilimindedir.

Kovaryans için negatif bir sayı, bir değişken artarken ikinci bir değişkenin azalma eğiliminde olduğunu gösterir. Örneğin, matematik ve tarihin negatif bir kovaryansı (-24,44) vardır, bu da matematikte yüksek puan alan öğrencilerin tarihte düşük puan alma eğiliminde olduğunu gösterir. Benzer şekilde, matematikte düşük puan alan öğrenciler tarihte de yüksek puan alma eğilimindedir.

Ek kaynaklar

Excel’de Kovaryans Matrisi Nasıl Oluşturulur
R’de kovaryans matrisi nasıl oluşturulur
Python’da Kovaryans Matrisi Nasıl Oluşturulur
SPSS’de Kovaryans Matrisi Nasıl Oluşturulur