Kritik değer
Bu makale istatistikte kritik değerin ne olduğunu ve hipotez testinde nasıl yorumlanması gerektiğini açıklamaktadır. Aynı şekilde kritik değerin nasıl hesaplandığını ve birkaç somut örneği görebileceksiniz.
Kritik değer nedir?
Kritik değer , test istatistiğinin dağılımında sıfır hipotezinin reddedildiği bölgeyi kabul edildiği bölgeden ayıran noktadır. Başka bir deyişle kritik değer, ret bölgesinin (veya kritik bölgenin) sınırını işaret eden istatistiksel testin dağılım değeridir.
Normalde kritik değer Zα /2 sembolüyle temsil edilir, çünkü en yaygın referans dağılımı genellikle standart normal dağılımdır .
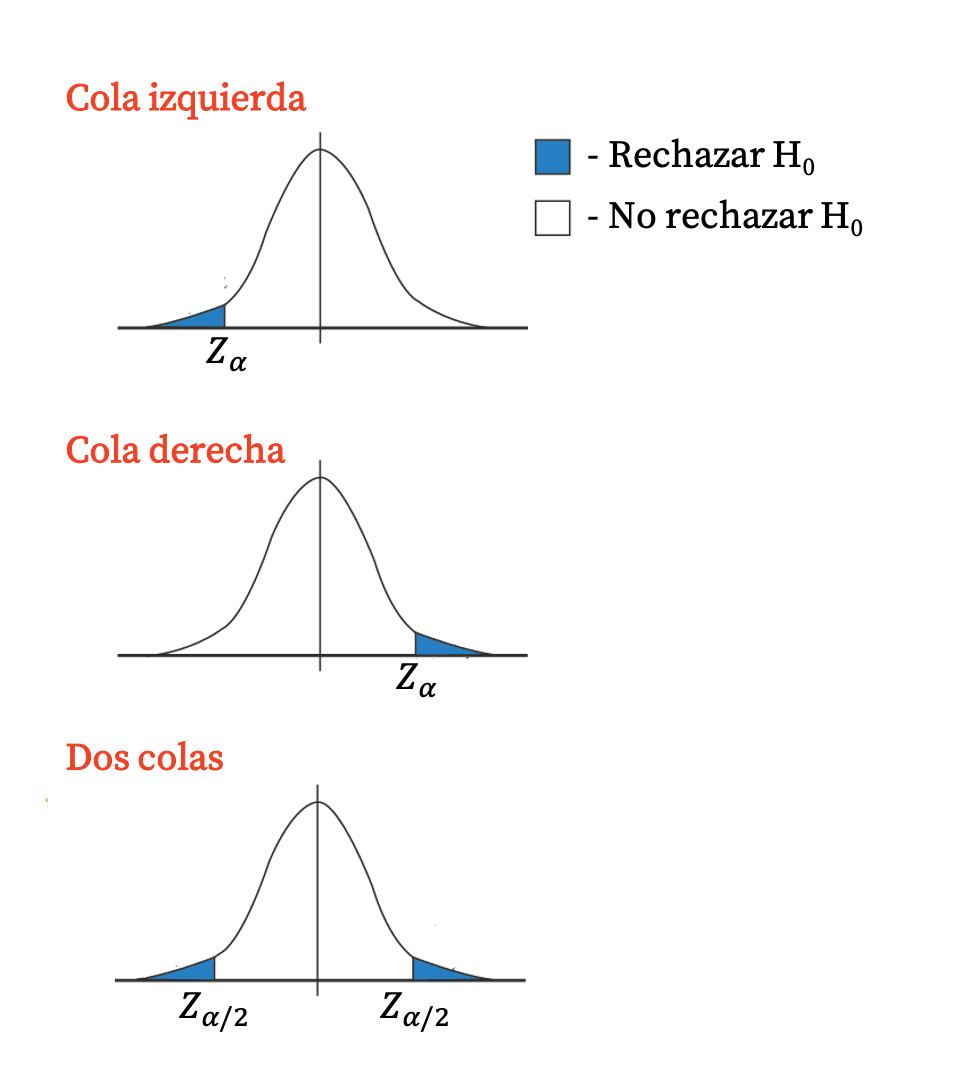
Reddetme bölgesi dağılımın tek kuyruğunu oluşturduğundan genel olarak tek taraflı testler kritik değere sahiptir. Öte yandan, iki kuyruklu testlerin iki kritik değeri vardır çünkü red bölgesi, dağılımın her iki kuyruğuna da karşılık gelir.
Güven aralıklarında kritik değerler, referans dağılımında güven aralığının sınırlarını işaretleyen noktalardır.
Kritik değer nasıl hesaplanır
Daha sonra en yaygın kritik değerlerin nasıl hesaplandığını göreceğiz. Ortalamanın güven aralığı için Z’nin kritik değeri ve t’nin kritik değeri hesaplanır, tek fark Z’nin kritik değerinin popülasyon standart sapması bilindiğinde hesaplanmasıdır ve bunun yerine t’nin kritik değeri kullanılır. yalnızca bir numunenin verileri bilindiğinde.
Z’nin kritik değeri
Z’nin kritik değeri ortalamanın güven aralığının sınırlarını belirlemek için kullanılır. Daha doğrusu, yalnızca popülasyon standart sapmasını biliyorsanız kullanılır.
Z’nin kritik değerini hesaplamak için standart normal dağılım tablosunda anlamlılık düzeyinin yarısı olasılığına karşılık gelen değerin bulunması gerekir.
Örneğin ortalama için %95 güven düzeyinde bir güven aralığı belirlemek istiyorsak bu, anlamlılık düzeyinin %5 olduğu anlamına gelir. Bu nedenle ortalamanın güven aralığı iki taraflı olduğundan standart normal dağılım tablosunda hangi değerin %2,5 olasılığa karşılık geldiğini görmek gerekir.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
Aşağıda en çok kullanılan kritik Z değerlerinin yer aldığı tabloyu görebilirsiniz:
| Güven düzeyi (1-α) | Önem düzeyi (α) | Kritik değer (Z α/2 ) |
|---|---|---|
| 0.80 | 0.20 | 1.282 |
| 0,85 | 0,15 | 1.440 |
| 0,90 | 0.10 | 1.645 |
| 0,95 | 0,05 | 1960 |
| 0,99 | 0,01 | 2.576 |
| 0,995 | 0,005 | 2.807 |
| 0,999 | 0,001 | 3.291 |
T’nin kritik değeri
Kritik t değeri, popülasyon standart sapmasının bilinmediği durumlarda ortalamaya ilişkin güven aralığının sınırlarını bulmak için kullanılır.
T’nin kritik değerini hesaplamak için, Öğrenci t dağılımının serbestlik derecesinin bir birim olduğu dikkate alınarak, Öğrenci t dağılım tablosunda anlamlılık düzeyinin yarısı olasılığına karşılık gelen değerin bulunması gerekir. örneklem boyutundan daha fazladır.
Örneğin güven aralığını %95 güven düzeyinde bulmak istiyorsak ve örneklem büyüklüğü 8 ise, Öğrenci t dağılım tablosuna erişmemiz ve hangi değerin t 0.025|7’ye karşılık geldiğini görmemiz gerekir.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-2caa8c4576ebc261acfdb1341dc4567d_l3.png)
Hipotez testinde kritik değer
Kritik değer aynı zamanda hipotez testinde sıfır hipotezini reddetmek (ve alternatif hipotezi kabul etmek) veya alternatif hipotezi reddetmek (ve sıfır hipotezini kabul etmek) için de kullanılabilir.
- P değerine karşılık gelen test istatistiğinin dağılım değeri, kritik değerlerle işaretlenen aralık içinde yer alıyorsa, sıfır hipotezi reddedilmez (alternatif hipotez reddedilir).
- Test istatistiğinin p değerine karşılık gelen dağılım değeri, kritik değerlerle işaretlenen aralığın dışındaysa sıfır hipotezi reddedilir (alternatif hipotez kabul edilir).