Python'da kübik regresyon nasıl gerçekleştirilir

Kübik regresyon, değişkenler arasındaki ilişki doğrusal olmadığında, bir yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanabileceğimiz bir regresyon türüdür.

Bu eğitimde Python’da kübik regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Python’da kübik regresyon

İki değişken (x ve y) içeren aşağıdaki panda DataFrame’e sahip olduğumuzu varsayalım:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Bu verinin basit bir dağılım grafiğini çıkarırsak iki değişken arasındaki ilişkinin doğrusal olmadığını görebiliriz:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

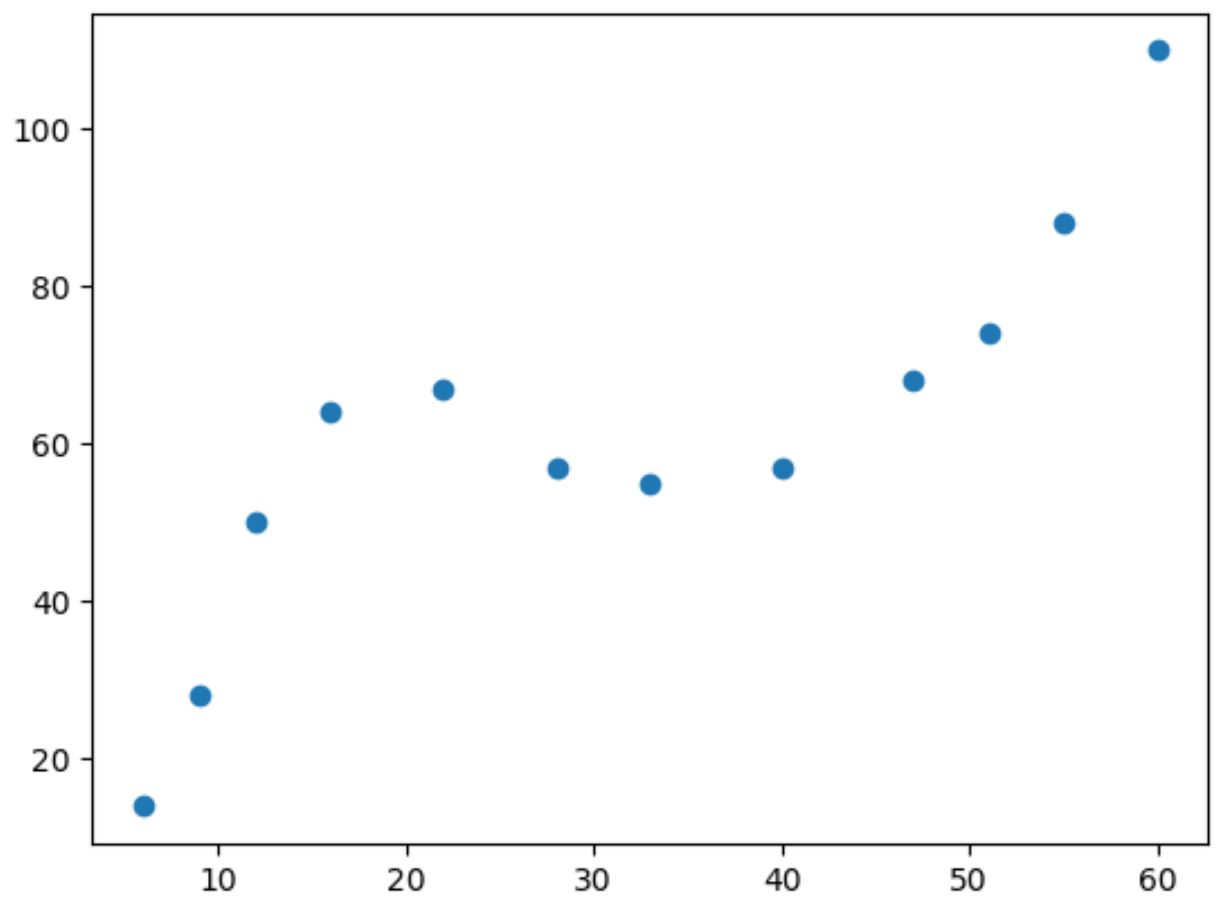
X’in değeri arttıkça y de belli bir noktaya kadar artar, sonra azalır, sonra tekrar artar.

Çizimde iki “eğri” bulunan bu model, iki değişken arasındaki kübik ilişkinin bir göstergesidir.

Bu, kübik regresyon modelinin iki değişken arasındaki ilişkiyi ölçmek için iyi bir aday olduğu anlamına gelir.

Kübik regresyon gerçekleştirmek için numpy.polyfit() işlevini kullanarak derece 3’e sahip bir polinom regresyon modeli yerleştirebiliriz:

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

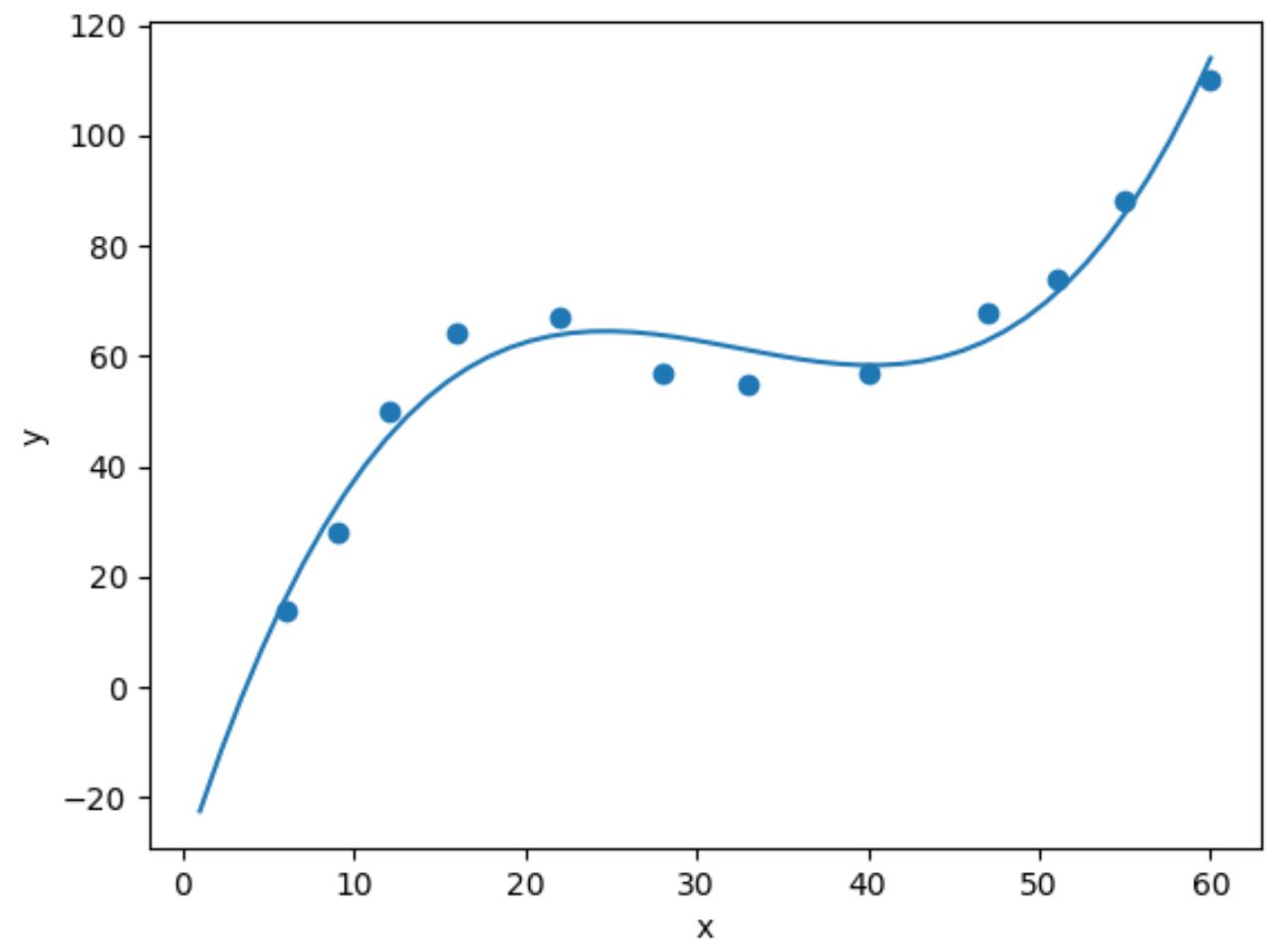
Uygun kübik regresyon denklemini model katsayılarını yazdırarak elde edebiliriz:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

Uygun kübik regresyon denklemi şöyledir:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Bu denklemi x’in değerine bağlı olarak y’nin beklenen değerini hesaplamak için kullanabiliriz.

Örneğin, x 30 ise y’nin beklenen değeri 64,844’tür:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Ayrıca, yordayıcı değişkenler tarafından açıklanabilen yanıt değişkenindeki varyansın oranı olan modelin R-karesini elde etmek için kısa bir fonksiyon da yazabiliriz.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

Bu örnekte modelin R karesi 0,9632’dir .

Bu, yanıt değişkenindeki değişimin %96,32’sinin yordayıcı değişken tarafından açıklanabileceği anlamına gelmektedir.

Bu değerin çok yüksek olması bize kübik regresyon modelinin iki değişken arasındaki ilişkiyi iyi ölçtüğünü söyler.

İlgili: İyi bir R-kare değeri nedir?

Ek kaynaklar

Aşağıdaki eğitimlerde Python’da diğer genel görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Python’da basit doğrusal regresyon nasıl gerçekleştirilir
Python’da ikinci dereceden regresyon nasıl gerçekleştirilir?
Python’da polinom regresyonu nasıl gerçekleştirilir