Kümülatif frekans

Bu makalede istatistiklerde kümülatif frekansın ne olduğu açıklanmaktadır. Böylece kümülatif frekansın anlamını, kümülatif frekansın nasıl hesaplandığını örneklerle ve son olarak da var olan farklı kümülatif frekans türlerini öğreneceksiniz.

Kümülatif frekans nedir?

İstatistikte kümülatif frekans , frekansların kümülatif toplamıdır. Yani bir değerin kümülatif frekansı, o değerin frekansı artı tüm alt değerlerin frekanslarının toplamına eşittir.

İki tür kümülatif frekans vardır: kümülatif mutlak frekans ve kümülatif bağıl frekans. Aşağıda her bir kümülatif frekans türünün nasıl hesaplandığını göreceğiz.

İstatistiklerde kümülatif frekansın ne anlama geldiğini anlamak için öncelikle frekans kavramı konusunda net olmanız gerektiğini unutmayın. Bu nedenle açıklamaya devam etmeden önce aşağıdaki yazıyı ziyaret etmeniz önerilir:

Kümülatif frekans nasıl hesaplanır

İstatistiksel bir örneğin kümülatif sıklığını hesaplama adımları şunlardır:

1. Veri kümesinde görünen tüm farklı değerlerin en küçükten en büyüğe doğru sıralandığı bir tablo oluşturun.
2. Her değerin mutlak frekansını bulun.
3. Her bir değerin kümülatif frekansını bulun; bu frekans, değerin kendisinin frekansı artı tüm küçük değerlerin frekansları toplanarak hesaplanır.

Bu nedenle kümülatif frekansı hesaplama formülü şöyledir:

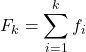
Altın:

• 

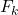
  değerin kümülatif frekansıdır

  

  .

• 

  değerin mutlak frekansıdır

  

  .

Bu adımların kümülatif mutlak frekansı hesaplamak için olduğunu ancak aynı zamanda kümülatif bağıl frekansın da bulunduğunu unutmayın. Aşağıda bu iki tür birikmiş frekans arasındaki farkı ve her türün nasıl bulunduğunu göreceğiz.

Kümülatif frekans türleri

İstatistikte iki tür kümülatif frekans vardır:

• Kümülatif mutlak frekans : Bu, mutlak frekansların kümülatif toplamıdır.
• Kümülatif bağıl frekans : bu, bağıl frekansların kümülatif toplamıdır.

Her bir birikmiş frekans türünün tanımı göz önüne alındığında, her birinin nasıl elde edildiğine dair bir örneği aşağıda görebilirsiniz.

Kümülatif mutlak frekans

Kümülatif mutlak frekans, F _i sembolü ile temsil edilir ve söz konusu değere eşit veya daha küçük değerlerin mutlak frekanslarının eklenmesiyle hesaplanır. Daha sonra, istatistiksel bir veri setinin kümülatif mutlak frekansının hesaplandığı somut bir örneğiniz var.

• 30 kişilik bir sınıfta istatistik konusunda alınan notlar aşağıdaki gibidir. Her notanın kümülatif mutlak frekansı nedir?

Tüm sayılar yalnızca tam sayı olabildiği için ayrık bir değişkendir. Bu nedenle verileri aralıklar halinde gruplamak gerekli değildir.

Dolayısıyla, kümülatif mutlak frekansı belirlemek için öncelikle her değerin mutlak frekansını bulmamız gerekir; bu, her bir değerin istatistiksel örnekte görünme sayısıdır.

Artık her değerin mutlak frekansını bildiğimize göre kümülatif mutlak frekanslarını hesaplayabiliriz. Bunu yapmak için iki seçeneğimiz var: ya değerin mutlak frekansı artı en küçük değerlerin tüm mutlak frekanslarını topluyoruz ya da tam tersine, değerin mutlak frekansı artı önceki değerlerin kümülatif mutlak frekansını topluyoruz . değer.

Kısaca mutlak kümülatif egzersiz sıklığını gösteren tablo şu şekildedir:

Son değerin birikmiş mutlak frekansının her zaman toplam veri sayısıyla çakıştığını unutmayın. Aksi halde hesaplamada hata yapmışsınız demektir.

Kümülatif bağıl frekans

Kümülatif bağıl frekans, H _i sembolü ile temsil edilir ve söz konusu değere eşit veya ondan daha düşük değerlerin bağıl frekanslarının eklenmesiyle hesaplanır. Aşağıda kümülatif bağıl frekansın belirlendiği önceki problemle aynı verilerle çözülmüş bir alıştırmayı görebilirsiniz.

• 30 kişilik bir sınıfta istatistikten alınan notlar aşağıdaki gibidir. Her notanın kümülatif bağıl frekansı nedir?

Bu durumda değişken ondalık değer alamadığı için ayrıktır. Yani verileri aralıklara göre gruplandırmaya gerek yok ama hesaplamaları doğrudan yapabiliyoruz.

Böylece bir frekans tablosu hazırlıyor ve her farklı değerin mutlak frekansını belirliyoruz:

Daha sonra, mutlak frekansın toplam gözlem sayısına (30) bölünmesiyle belirlenen her bir değerin göreceli frekansını hesaplıyoruz.

Veri setinin mutlak frekansını ve bağıl frekansını hesapladıktan sonra kümülatif bağıl frekansı elde edebiliriz. Bunu yapmak için, söz konusu değerin göreceli frekansını artı tüm önceki göreceli frekansları veya aynı anlama gelen önceki birikmiş göreceli frekansı eklemelisiniz:

Kısaca mutlak frekans, bağıl frekans ve kümülatif bağıl frekansın yer aldığı frekans tablosu şu şekildedir:

Kümülatif bağıl frekansın son değerinin her zaman 1 olması gerektiğini unutmayın. Başka bir sayı alırsanız hesaplamalarda hata yapmışsınız demektir.