Bir kutu grafiğinin çeyrekler arası aralığı (iqr) nasıl bulunur?

Kutu grafiği, aşağıdakileri içeren bir veri kümesinin beş basamaklı özetini görüntüleyen bir grafik türüdür:

• Asgari değer
• İlk çeyrek (25. yüzdelik dilim)
• Medyan değer
• Üçüncü çeyrek (75. yüzdelik dilim)
• Maksimum değer

Bir kutu grafiği oluşturmak için birinci çeyrekten üçüncü çeyreğe kadar bir kutu çizeriz. Daha sonra ortancaya dikey bir çizgi çiziyoruz. Son olarak çeyreklerin “bıyıklarını” minimum ve maksimum değere kadar çiziyoruz.

Genellikle IQR olarak kısaltılan çeyrekler arası aralık , üçüncü çeyrek ile birinci çeyrek arasındaki farktır.

• IQR = Ç3 – Ç1

Bu bize belirli bir veri setindeki değerlerin ortadaki %50’lik dağılımını anlatır.

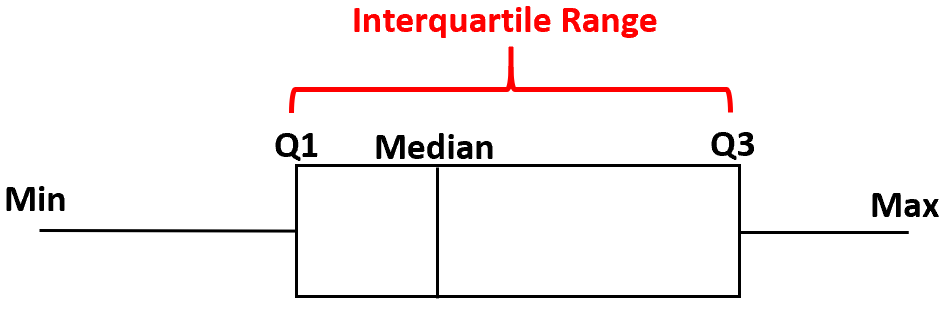
Aşağıdaki örnekler, pratikte bir kutu grafiğinin çeyrekler arası aralığının (IQR) nasıl bulunacağını göstermektedir.

Örnek 1: Sınav sonuçları

Aşağıdaki kutu grafiği belirli bir üniversite sınavındaki puanların dağılımını göstermektedir. Test puanlarının çeyrekler arası aralığı nedir?

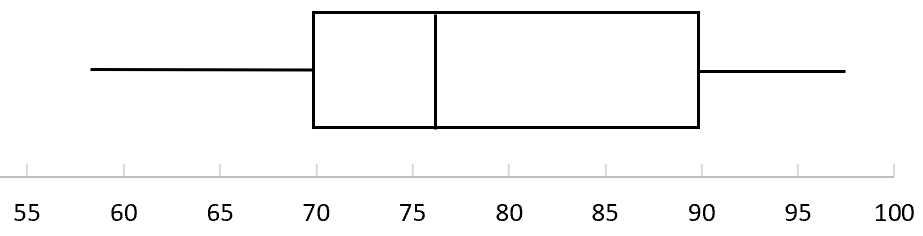
Bu soruyu cevaplamak için kutu grafiğinde aşağıdaki değerleri bulabiliriz:

• Ç3 (üst çeyrek) = 90
• Q1 (alt çeyrek) = 70
• Çeyrekler arası ölçek (IQR) = 90 – 70 = 20

İnceleme sonuçlarının çeyrekler arası aralığı 20’dir .

Örnek 2: Kazanılan puanlar

Aşağıdaki kutu grafiği belirli bir ligde basketbolcuların attığı puanların dağılımını göstermektedir. Dağılımın çeyrekler arası aralığı nedir?

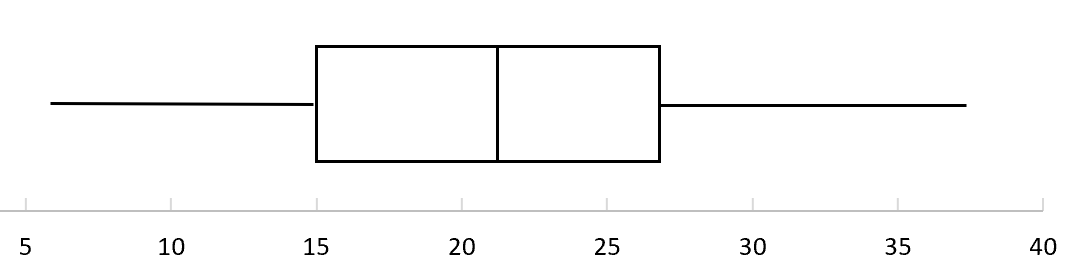
Bu soruyu cevaplamak için kutu grafiğinde aşağıdaki değerleri bulabiliriz:

• Q3 (Üst çeyrek) = 27
• Q1 (alt çeyrek) = 15
• Çeyrekler arası ölçek (IQR) = 27 – 15 = 12

Dağılımın çeyrekler arası aralığı 12’dir .

Örnek 3: Bitki boylarının karşılaştırılması

Aşağıdaki kutu grafikleri iki farklı bitki türü için yükseklik dağılımını göstermektedir: kırmızı ve mavi. Hangi dağılımın çeyrekler arası aralığı daha büyüktür?

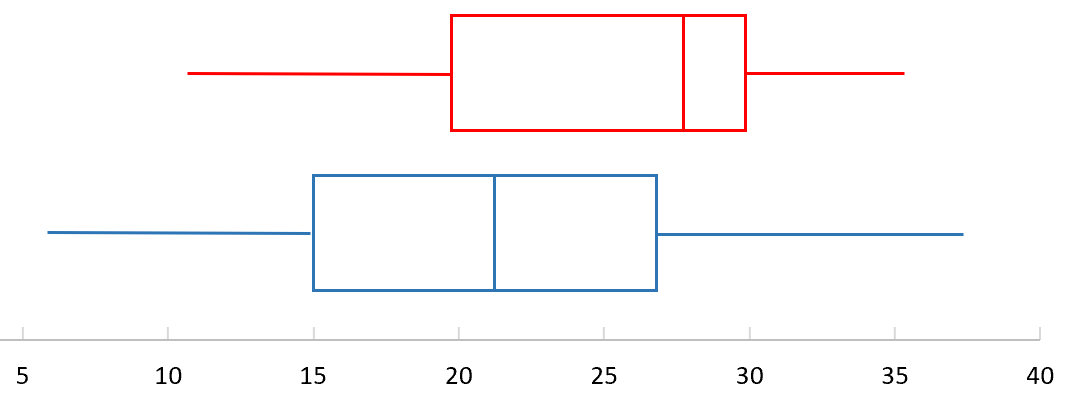
İlk önce kırmızı kutunun çeyrekler arası aralığını bulalım:

• Ç3 (üst çeyrek) = 30
• Ç1 (alt çeyrek) = 20
• Çeyrekler arası ölçek (IQR) = 30 – 20 = 10

Sonra mavi kutu grafiğinin çeyrekler arası aralığını bulalım:

• Q3 (Üst çeyrek) = 27
• Q1 (alt çeyrek) = 15
• Çeyrekler arası ölçek (IQR) = 27 – 15 = 12

Mavi türler için çeyrekler arası aralık daha büyüktür.

Ek kaynaklar

Aşağıdaki eğitimler kutu grafikleri hakkında ek bilgi sağlar:

Kutu Çizimi Oluşturucu
Kutu Grafikleri Nasıl Karşılaştırılır
Kutu Grafiklerinde Asimetri Nasıl Belirlenir?
Çeyrekler arası aralık nasıl yorumlanır?