Kutu ve bıyık grafiği

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede, kutu grafiği (veya kutu grafiği) olarak da bilinen kutu grafiğinin ne olduğu açıklanmaktadır. Bu tür istatistiksel diyagramların nasıl yapıldığını ve kutu ve bıyık diyagramının çözülmüş bir alıştırmasını ve yorumunu keşfedeceksiniz.

Kutu ve bıyık grafiği nedir?

Kutu grafiği veya kutu grafiği olarak da adlandırılan kutu grafiği, çeyrekler kullanarak bir dizi istatistiksel veriyi görsel olarak temsil eden bir grafiktir.

Kutu ve bıyık grafiğinin ana özelliği, verilerin çeyreklerini, medyanını, uç değerlerini ve aykırı değerlerini gösterdiği için bir dizi verinin dağılımını hızlı bir şekilde görselleştirmenize olanak sağlamasıdır.

Dolayısıyla, bu tür bir diyagram, dikdörtgen bir kutu ve aşağıdaki değerlerin ortaya çıktığı birkaç çizgiden (veya bıyıktan) oluşur:

Kutunun sınırları birinci ve üçüncü çeyrekleri (Q ₁ ve Q ₃ ) gösterir. Ve kutunun içindeki dikey çizgi medyandır (ikinci çeyrek _Q2’ye eşdeğerdir).
Bıyıkların (veya kolların) sınırları uç değerlerdir , yani veri serisinin minimum değeri ve maksimum değeridir.
Bıyıkların dışındaki noktalar aykırı değerlerdir, yani muhtemelen yanlış ölçülmüş olan ve bu nedenle istatistiksel çalışmada dikkate alınmaması gereken verilerdir.

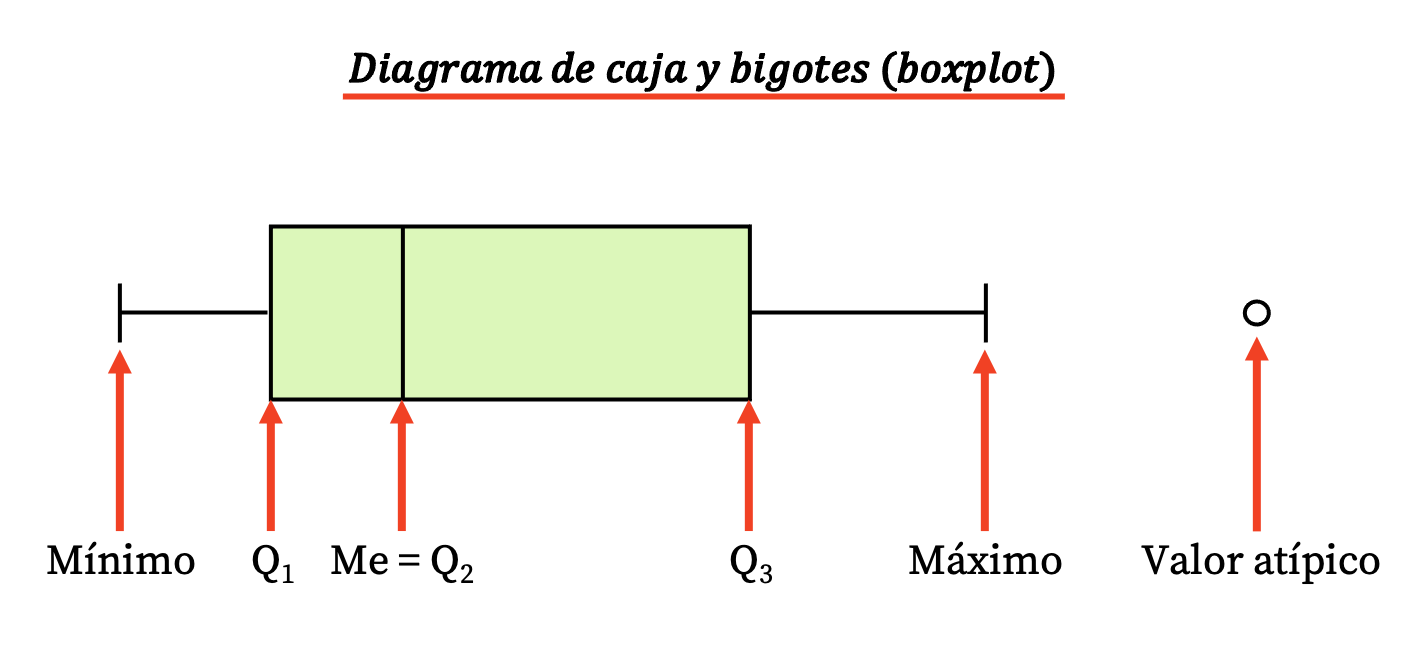
Üçüncü ve birinci çeyrek arasındaki farkın, istatistiksel dağılımın başka bir ölçüsü olan çeyrekler arası aralık (veya çeyrekler arası aralık) olduğuna dikkat edin.

Kutu ve bıyık grafikleri sayısal değişkenleri karşılaştırmak için çok faydalıdır. Ancak kategorik değişkenleri temsil etmeye uygun değildir.

Kutu ve Bıyık Grafiği Nasıl Oluşturulur

Bir veri serisinden bir kutu ve bıyık grafiği (veya kutu grafiği) oluşturmak için aşağıdaki adımlar gerçekleştirilmelidir:

İstatistiksel veri örneklerini sıralayın.
Çeyrekleri (Q ₁ , Q ₂ ve Q ₃ ) hesaplayın ve bunları diyagramdaki kutu olarak gösterin. Birinci ve üçüncü çeyrekler kutunun sınırlarına karşılık gelir ve medyanı (ikinci çeyrek) temsil etmek için kutunun içine, değerinin bulunduğu yere bir çizgi çizmeniz gerekir.
Üçüncü çeyrekten birinci çeyreğe eşit olan çeyrekler arası aralığı hesaplayın.

$IQR=Q_3-Q_1$

Formülleri aşağıdaki gibi kabul edilebilir LI ve LS değerlerini hesaplayın:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

LI’den küçük veya LS’den büyük değerler olan örnek aykırı değerleri belirleyin. Bıyık aralığının dışındaki bu değerleri noktalarla temsil edin.
LI ve LS’nin oluşturduğu aralıktaki en küçük değer ve en büyük değer olan uç değerleri belirleyin ve temsil edin. Bu değerler diyagramdaki iki bıyığın sonunu temsil etmektedir.

Kutu ve Bıyık Grafiği Örneği

Kutu ve bıyık grafiğinin (veya kutu grafiğinin) tanımını ve teorisini göz önünde bulundurarak, kavramı daha iyi anlamak ve bu tür istatistiksel grafiğin nasıl yürütüldüğünü görmek için aşağıda somut bir örnek bulacaksınız.

Aşağıdaki istatistiksel veri setinin kutu grafiğini çizin.

Bu durumda veriler zaten en küçükten en büyüğe doğru sıralanmıştır, dolayısıyla herhangi bir değişiklik yapılmasına gerek yoktur. Aksi halde öncelikle örnek verileri sıralamamız gerekir.

İkinci olarak, numunenin çeyreklerini çıkarıyoruz:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ Bakınız: çeyrek hesaplayıcı

Üç çeyreği hesapladıktan sonra çeyrekler arası aralığı, çeyrek 3 eksi çeyrek 1’i çıkararak buluruz:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

Artık verilerin atipik olarak kabul edildiği değerler olan LI ve LS limitlerini hesaplıyoruz. Bunu yapmak için aşağıdaki formülleri kullanmanız gerekir:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

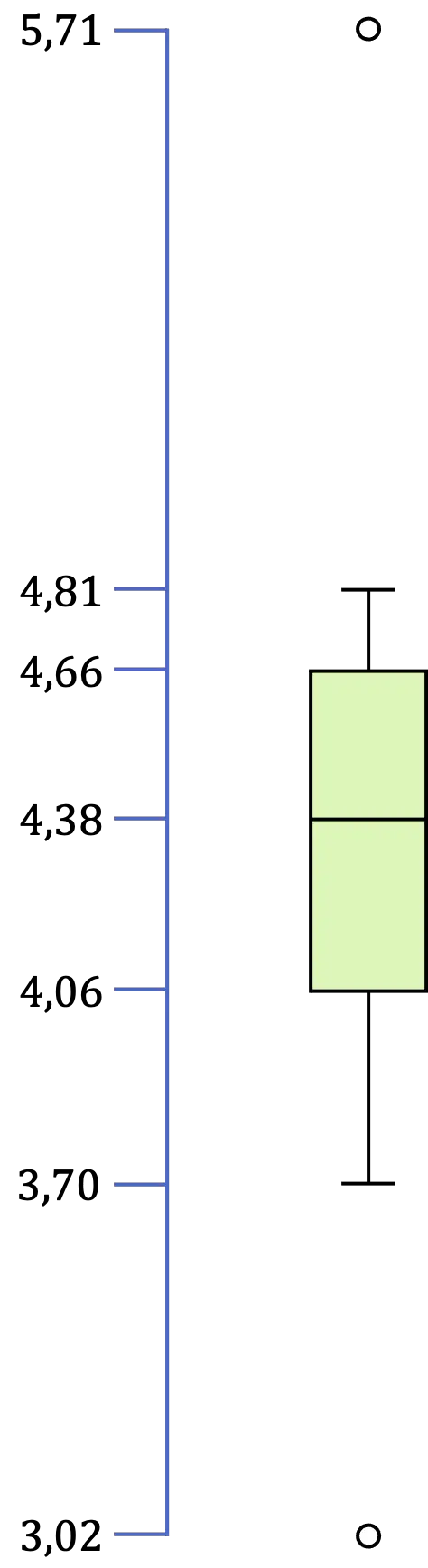
Yani bu durumda iki aykırı değerimiz var çünkü 3,02, 3,16’dan küçük ve 5,71, 5,56’dan büyük.

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

Son olarak, [LI,LS] aralığındaki tüm verilerin minimum ve maksimumu olan uç değerlerin belirlenmesi kalır. Dolayısıyla örneğimizde minimum değer 3,70, maksimum değer ise 4,81’dir.

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

Yani, kutunun ve bıyık grafiğinin tüm değerlerini belirledikten sonra geriye kalan tek şey grafiksel gösterimi yapmaktır:

Kutu ve bıyık grafiği ne için kullanılır?

Son olarak bunun ne işe yaradığına ve kutu ve bıyık grafiğinin (veya kutu grafiğinin) nasıl yorumlanacağına bakalım.

Açıkçası, kutu ve bıyık grafiği, bir veri serisinin çeyreklerini, çeyrekler arası aralığını, medyanını, uç değerlerini ve aykırı değerlerini hızlı bir şekilde bilmek için çok faydalıdır, çünkü tüm bu istatistiksel ölçümler basit bir bakışla tanımlanabilir.

Ek olarak, tüm veri setini görsel olarak temsil ettiğinden istatistiksel numunenin simetrisini analiz etmek için kutu ve bıyık grafiği kullanılır. Ortanca kutunun ortasında değilse bu, numunenin simetrik olmadığı anlamına gelir.

Benzer şekilde, kısa bir süre içinde maksimum değer, minimum değer ve ara değerlerin görülmesine olanak tanıdığından, bir hisse senedinin belirli bir süre içindeki fiyatındaki değişimi temsil etmek için borsada kutu grafikleri yaygın olarak kullanılmaktadır. zaman kazanır ve böylece daha hızlı kararlar alırsınız.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil