Tam kılavuz: excel'de anova sonuçları nasıl yorumlanır?

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Aşağıdaki örnek, Excel’de tek yönlü ANOVA sonuçlarının nasıl yorumlanacağına ilişkin eksiksiz bir kılavuz sağlar.

Örnek: Excel’de ANOVA sonuçları nasıl yorumlanır?

Bir öğretmenin sınıfındaki 30 öğrenciden rastgele bir sınava hazırlanmak için üç çalışma yönteminden birini kullanmalarını istediğini varsayalım.

Aşağıdaki ekran görüntüsü öğrencilerin kullandıkları yönteme göre aldıkları puanları göstermektedir:

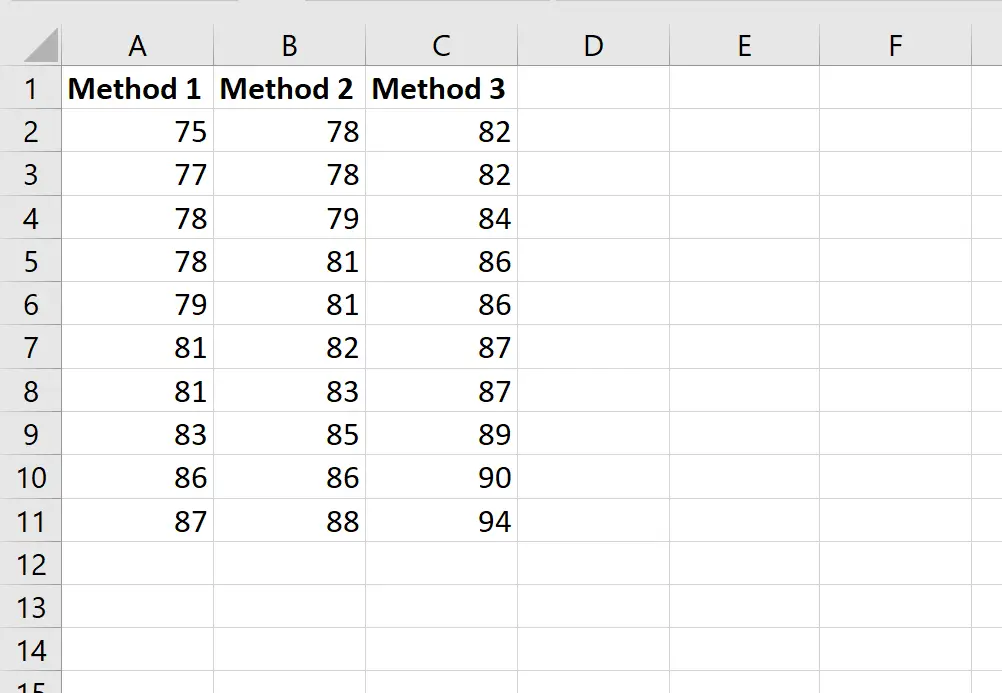
Öğretmenin ortalama puanların üç grup arasında aynı olup olmadığını belirlemek için tek yönlü bir ANOVA yapmak istediğini varsayalım.

Excel’de tek yönlü ANOVA gerçekleştirmek için üst şeritteki Veri sekmesine tıklayın ve ardından Analiz grubunda Veri Analizi’ne tıklayın.

Veri Analizi seçeneğini göremiyorsanız , öncelikle ücretsiz Analiz Araç Paketi yazılımını yüklemelisiniz .

Üzerine tıkladığınızda yeni bir pencere görünecektir. Anova: Tek Faktör’ü seçin ve ardından Tamam’a tıklayın.

Açılan yeni pencerede aşağıdaki bilgileri girin:

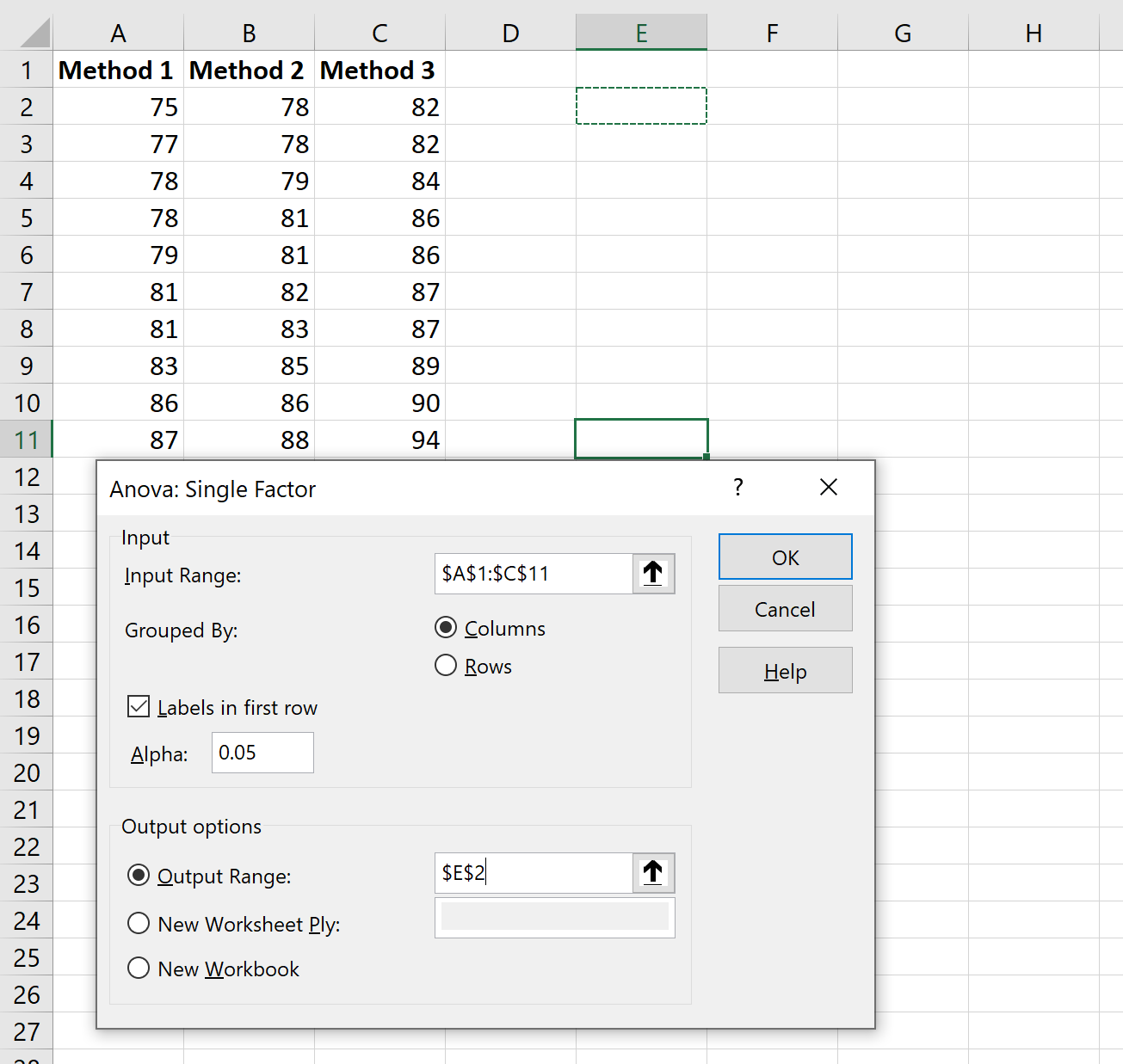
Tamam’a tıkladığınızda tek yönlü ANOVA sonuçları görünecektir:

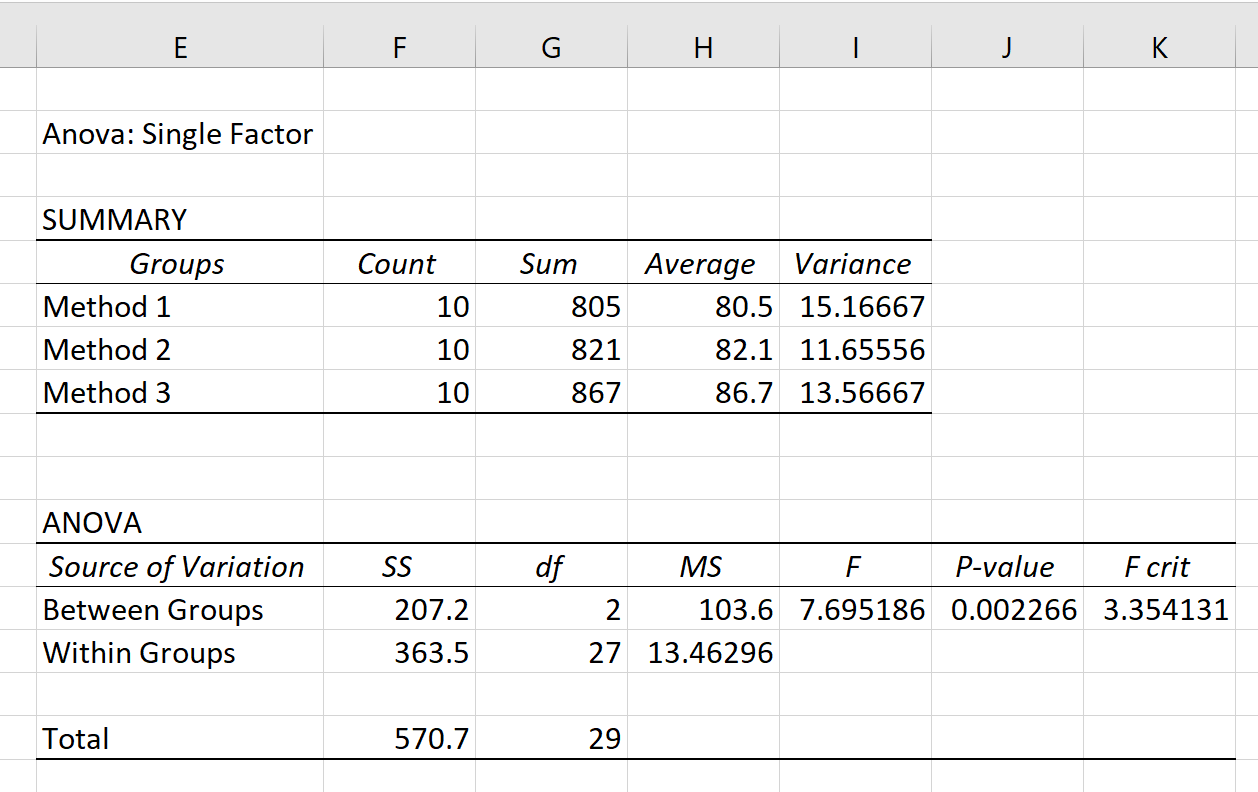
Sonuçta iki tablo görüntülenir: SUMMARY ve ANOVA .

Her tablodaki değerleri şu şekilde yorumlayabilirsiniz:

ÖZET tablosu :

• Gruplar : Grup adları
• Sayım : Her gruptaki gözlem sayısı
• Sum : Her grubun değerlerinin toplamı
• Ortalama : Her gruptaki ortalama değer
• Varyans : Her gruptaki değerlerin varyansı

Bu tablo bize ANOVA’da kullanılan her grup için çeşitli yararlı özet istatistikler sağlar.

Bu tablodan, Yöntem 3’ü kullanan öğrencilerin en yüksek ortalama sınav puanına (86,7) sahip olduklarını ancak aynı zamanda test puanlarında da en yüksek varyansa sahip olduklarını görebiliriz. inceleme (13.56667).

Grup ortalamalarındaki farklılıkların istatistiksel olarak anlamlı olup olmadığını belirlemek için ANOVA tablosuna bakmamız gerekir.

ANOVA tablosu :

• Değişimin kaynağı : Ölçülen varyasyon (gruplar arasında veya gruplar içinde)
• SS : Her bir varyasyon kaynağı için karelerin toplamı
• df : Serbestlik dereceleri, df Arasında ve #gözlemler için #gruplar-1 olarak hesaplanır – df İçi için #gruplar
• MS : SS/sd cinsinden hesaplanan ortalama kareler toplamı
• F : MS Arasında / MS İçinde olarak hesaplanan genel F değeri
• P değeri : Genel F değerine karşılık gelen p değeri
• F crit : α = 0,05’e karşılık gelen kritik F değeri

Bu tablodaki en önemli değer, 0,002266 olarak ortaya çıkan p değeridir .

Tek yönlü bir ANOVA’nın aşağıdaki boş ve alternatif hipotezleri kullandığını hatırlayın:

• H ₀ : Tüm grup ortalamaları eşittir.
• H _A : Tüm grup ortalamaları eşit değildir.

P değeri α = 0,05’ten küçük olduğundan, tek yönlü ANOVA’nın boş hipotezini reddediyoruz ve tüm grup ortalamalarının eşit olmadığını belirtmek için yeterli kanıta sahip olduğumuz sonucuna varıyoruz.

Bu, üç çalışma yönteminin hepsinin aynı ortalama sınav notlarına yol açmadığı anlamına gelir.

Not : Sıfır hipotezini reddetmeniz gerekip gerekmediğini belirlemek için genel F değerini kritik F değeriyle de karşılaştırabilirsiniz. Bu durumda F’nin genel değeri F’nin kritik değerinden büyük olduğundan sıfır hipotezini reddederiz. P-değeri yaklaşımının ve kritik F-değeri yaklaşımının her zaman aynı sonuca varacağını unutmayın.

Ek kaynaklar

Aşağıdaki eğitimlerde Excel’de farklı ANOVA’ların nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir
Excel’de İki Yönlü ANOVA Nasıl Gerçekleştirilir
Excel’de Tekrarlanan Ölçümler ANOVA Nasıl Gerçekleştirilir
Excel’de Yuvalanmış ANOVA Nasıl Gerçekleştirilir