Spss'de levene testi nasıl yapılır?

Levene testi, iki veya daha fazla grubun eşit varyansa sahip olup olmadığını belirlemek için kullanılır.

Yaygın olarak kullanılmaktadır çünkü birçok istatistiksel test, grupların eşit varyanslara sahip olduğu varsayımına dayanmaktadır.

Bu eğitimde SPSS’de Levene testinin nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de Levene testi

Araştırmacılar, üç farklı gübrenin farklı bitki büyümesi düzeylerine yol açıp açmadığını bilmek istiyorlar.

Rastgele 30 farklı bitki seçiyorlar ve bunları 10’arlı üç gruba ayırıyorlar ve her gruba farklı bir gübre uyguluyorlar. Bir ay sonra her bitkinin yüksekliğini ölçüyorlar.

Aşağıdaki ekran görüntüsü, bitkiye uygulanan gübre (1, 2 veya 3) ile birlikte her bir bitki için büyüme miktarını (inç cinsinden) gösterir:

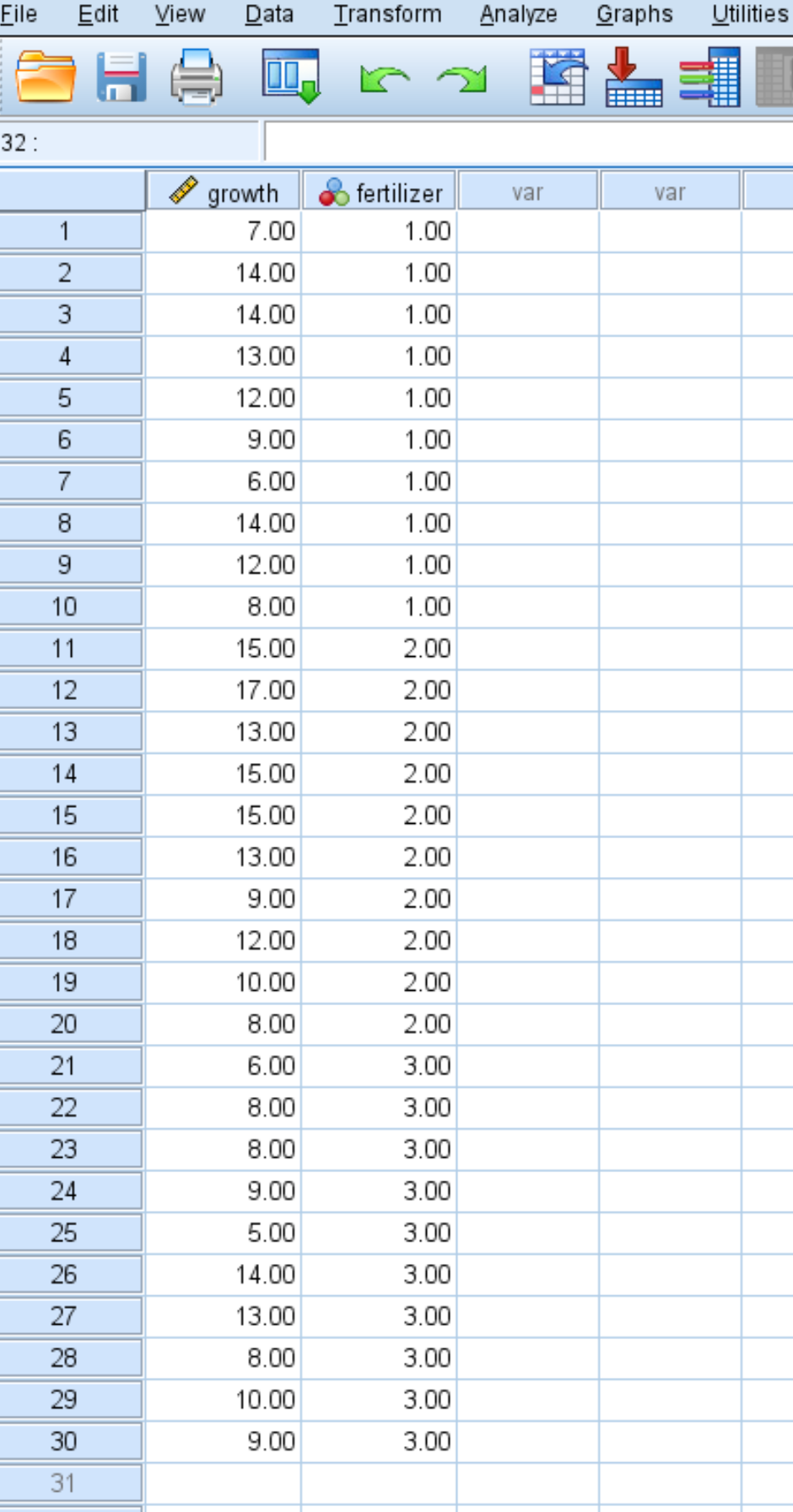
Üç grubun varyanslarının eşit olup olmadığını belirlemek amacıyla SPSS’de Levene testini gerçekleştirmek için aşağıdaki adımları izleyin.

Adım 1: Keşfet seçeneğini seçin.

Analiz sekmesini, ardından Tanımlayıcı İstatistikler’i ve ardından Keşfet’i tıklayın:

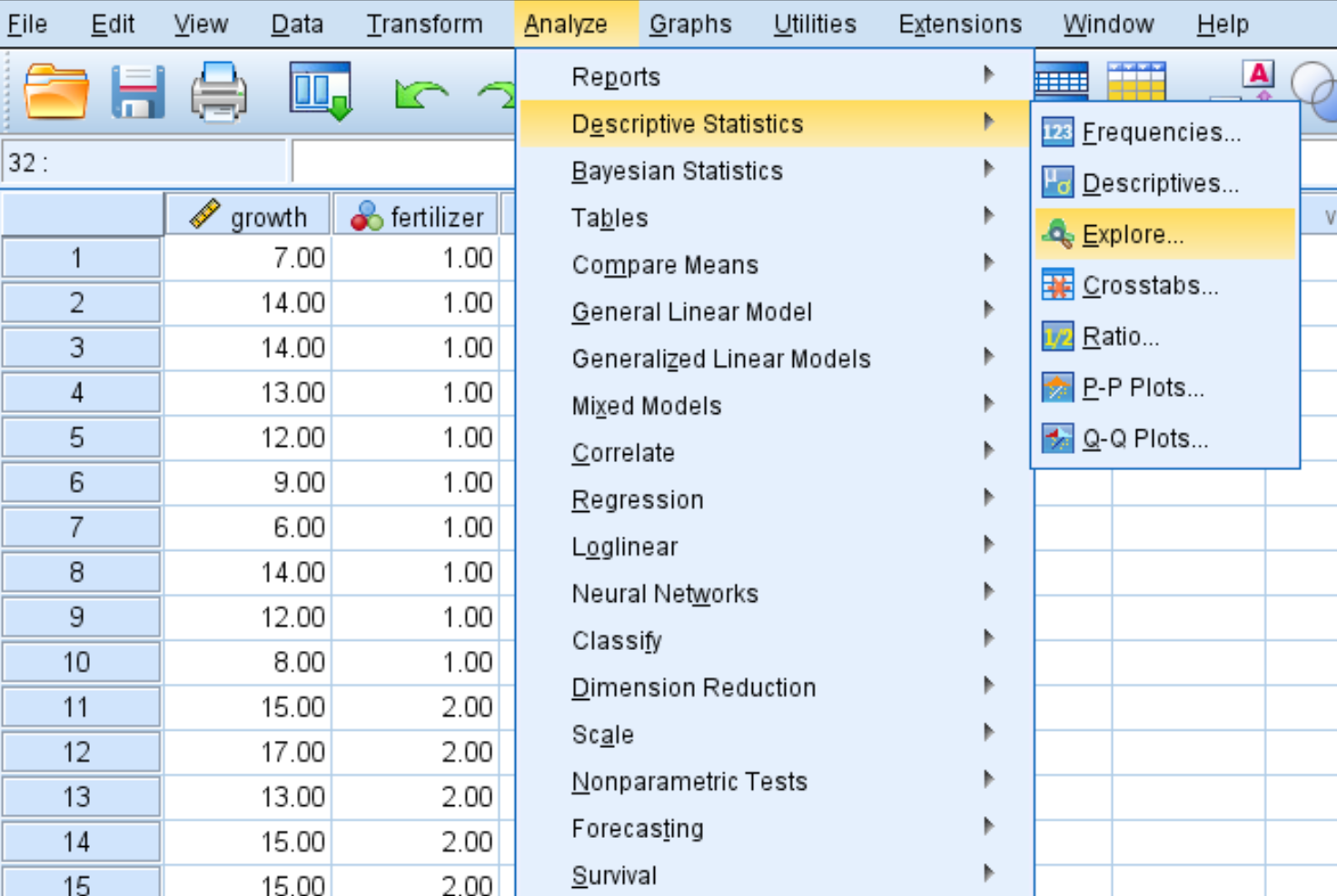
Adım 2: Testi gerçekleştirmek için gerekli değerleri girin.

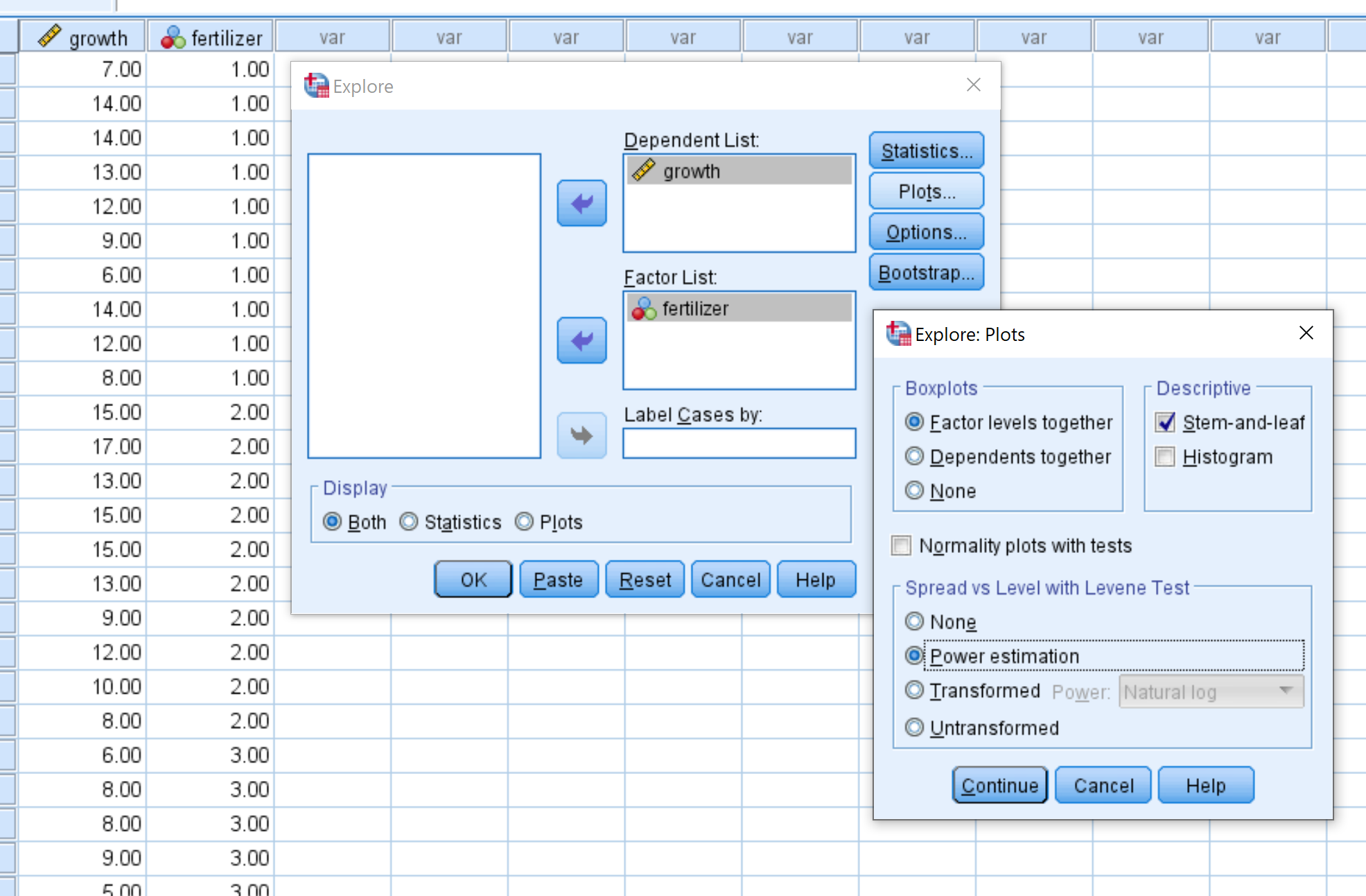
Büyümeyi Bağımlı Liste altındaki kutuya sürükleyin ve gübrelemeyi sürükleyin   Faktör Listesi altındaki kutuda.

Ardından Grafikler’e tıklayın ve Güç Tahmininin seçildiğinden emin olun. Daha sonra devam et’i tıklayın. Daha sonra Tamam’ı tıklayın.

Adım 3: Sonuçları yorumlayın.

Tamam’a tıkladığınızda Levene test sonuçları görüntülenecektir:

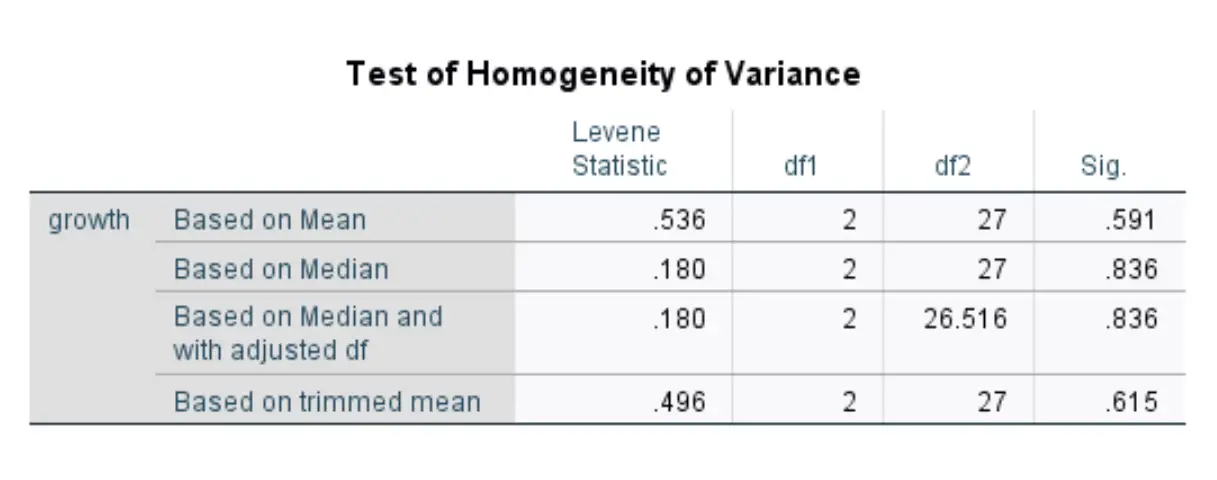
Bu tablo Levene testinin dört farklı versiyonuna ilişkin test istatistiklerini görüntüler. İlgilendiğimiz sayılar ortalamaya dayalı Levene testinin sonuçlarını gösteren ilk satırda yer almaktadır.

Test istatistiği 0,536’dır ve karşılık gelen p değeri 0,591*’ dir.

Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.

Bu, üç gübre arasındaki bitki büyümesindeki farklılığın önemli ölçüde farklı olduğunu söylemek için yeterli kanıta sahip olmadığımız anlamına geliyor.

Başka bir deyişle, üç grubun varyansları eşittir. Her grubun eşit varyansa sahip olduğunu varsayan istatistiksel bir test ( tek yönlü ANOVA gibi) yapsaydık, bu varsayım karşılanırdı.

* Bu p değeri, payı df = 2 ve paydası df = 27 olan 0,536’lık bir F istatistiğine karşılık gelir. Bu p değeri , F dağılımı hesaplayıcısı kullanılarak da hesaplanabilir.