Lojistik regresyon

İle Dr.benjamin anderson Ağustos 2, 2023 İstatistik 0 Yorum

Bu makale istatistikte lojistik regresyonun ne olduğunu açıklamaktadır. Benzer şekilde, lojistik regresyon formülünü, farklı lojistik regresyon türlerinin neler olduğunu ve ayrıca çözülmüş bir lojistik regresyon alıştırmasını bulacaksınız.

Lojistik regresyon nedir?

İstatistikte lojistik regresyon , kategorik bir değişkenin sonucunu tahmin etmek için kullanılan bir tür regresyon modelidir. Yani, kategorik bir değişkenin bağımsız değişkenlere göre belirli bir değer alma olasılığını modellemek için lojistik regresyon kullanılır.

En yaygın lojistik regresyon modeli, yalnızca iki olası sonucun olduğu ikili lojistik regresyondur: “başarısızlık” veya “başarı” ( Bernoulli dağılımı ). “Başarısızlık” 0 değeriyle, “başarı” ise 1 değeriyle temsil edilir.

Örneğin bir öğrencinin ders çalışarak geçirdiği saatlere göre sınavı geçme olasılığı lojistik regresyon modeli kullanılarak incelenebilir. Bu durumda başarısızlık “başarısızlığın” sonucu, başarı ise “başarı”nın sonucu olacaktır.

Lojistik Regresyon Formülü

Lojistik regresyon modelinin denklemi şöyledir:

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

Dolayısıyla lojistik regresyon modelinde “başarılı” sonucunun yani bağımlı değişkenin 1 değerini alması olasılığı aşağıdaki formülle hesaplanır:

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

Altın:

$p$

bağımlı değişkenin 1 olma olasılığıdır.
$\beta_0$

lojistik regresyon modelinin sabitidir.
$\beta_i$

i değişkeninin regresyon katsayısıdır.
$x_i$

i değişkeninin değeridir.

Lojistik Regresyon Modeli Örneği

Artık lojistik regresyonun tanımını bildiğimize göre, bu tür bir regresyon modelinin nasıl oluşturulacağına dair somut bir örnek görelim.

Aşağıdaki tabloda, her öğrencinin çalışma saatleri ve bir istatistik sınavını geçip geçmediği ile ilgili 20 parçalık bir veri dizisi derlenmiştir. Lojistik regresyon modelini çalıştırın ve bir öğrencinin 4 saat çalışması durumunda başarılı olma olasılığını hesaplayın.

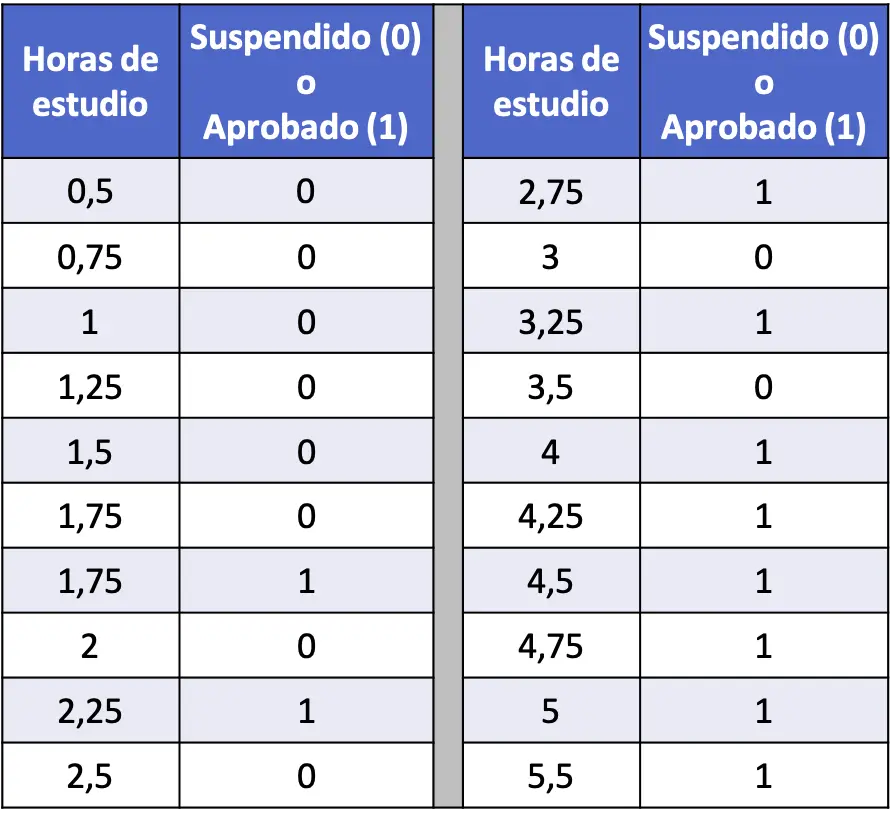
Bu durumda açıklayıcı değişken, çalışma saati sayısıdır ve yanıt değişkeni, öğrencinin başarısız olup olmadığı (0) veya başarılı olup olmadığıdır (1). Bu nedenle modelimizde sadece katsayıya sahip olacağız.

$\beta_0$

ve katsayı

$\beta_1$

Çünkü tek bir bağımsız değişken vardır.

$\beta_0 \qquad \beta_1$

Regresyon katsayılarının manuel olarak belirlenmesi oldukça zahmetli olduğundan Minitab gibi bilgisayar yazılımlarının kullanılması tavsiye edilir. Böylece Minitab kullanılarak hesaplanan regresyon katsayılarının değerleri aşağıdaki gibidir:

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

Dolayısıyla lojistik regresyon modeli aşağıdaki gibidir:

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

Aşağıda örnek verileri ve lojistik regresyon modeli denkleminin grafiğini görebilirsiniz:

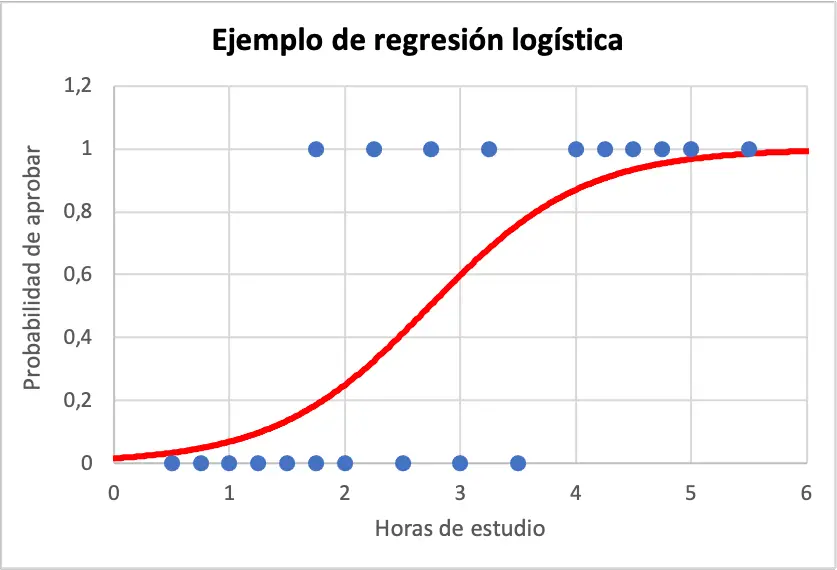
Bu nedenle, bir öğrencinin 4 saat çalışması durumunda başarılı olma olasılığını hesaplamak için lojistik regresyon modelinden elde edilen denklemi kullanmanız yeterlidir:

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

Kısaca bir öğrenci dört saat ders çalışırsa sınavı geçme ihtimali %86,99 olacaktır.

Lojistik Regresyon Türleri

Üç tür lojistik regresyon vardır:

İkili Lojistik Regresyon : Bağımlı değişken yalnızca iki değere (0 ve 1) sahip olabilir.
Çok terimli lojistik regresyon : Bağımlı değişkenin ikiden fazla olası değeri vardır.
Sıralı lojistik regresyon : olası sonuçların doğal bir sırası vardır.

Lojistik regresyon ve doğrusal regresyon

Son olarak özetle lojistik regresyon ile doğrusal regresyon arasındaki farkın ne olduğunu göreceğiz, çünkü istatistikte en çok kullanılan regresyon modeli doğrusal modeldir.

Sayısal bağımlı değişkenleri modellemek için doğrusal regresyon kullanılır. Ek olarak doğrusal regresyonda açıklayıcı değişkenler ile yanıt değişkeni arasındaki ilişki doğrusaldır.

Bu nedenle lojistik regresyon ile doğrusal regresyon arasındaki temel fark bağımlı değişkenin türüdür. Lojistik regresyonda bağımlı değişken kategoriktir, doğrusal regresyonda ise bağımlı değişken sayısaldır.

Bu nedenle, lojistik regresyon iki olası seçenek arasındaki sonucu tahmin etmek için kullanılırken, doğrusal regresyon sayısal bir sonucu tahmin etmeye yardımcı olur.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil