Python'da lojistik regresyon nasıl gerçekleştirilir (adım adım)

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullanabileceğimiz bir yöntemdir.

Lojistik regresyon, aşağıdaki formdaki bir denklemi bulmak için maksimum olabilirlik tahmini olarak bilinen bir yöntemi kullanır:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Altın:

• X _j : ^j’inci tahmin değişkeni
• β _j : ^j’inci yordayıcı değişkenin katsayısının tahmini

Denklemin sağ tarafındaki formül, yanıt değişkeninin 1 değerini almasına ilişkin log olasılığını tahmin eder.

Dolayısıyla, bir lojistik regresyon modeli uydurduğumuzda, belirli bir gözlemin 1 değerini alma olasılığını hesaplamak için aşağıdaki denklemi kullanabiliriz:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Daha sonra gözlemi 1 veya 0 olarak sınıflandırmak için belirli bir olasılık eşiği kullanırız.

Örneğin olasılığı 0,5’ten büyük veya ona eşit olan gözlemlerin “1”, diğer tüm gözlemlerin ise “0” olarak sınıflandırılacağını söyleyebiliriz.

Bu eğitimde, R’de lojistik regresyonun nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

Adım 1: Gerekli paketleri içe aktarın

Öncelikle Python’da lojistik regresyon gerçekleştirmek için gerekli paketleri içe aktaracağız:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

2. Adım: Verileri yükleyin

Bu örnek için, Introduction to Statistical Learning kitabındaki varsayılan veri kümesini kullanacağız. Veri kümesinin özetini yüklemek ve görüntülemek için aşağıdaki kodu kullanabiliriz:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Bu veri seti 10.000 kişiye ilişkin aşağıdaki bilgileri içermektedir:

• Varsayılan: Bir kişinin temerrüde düşüp düşmediğini gösterir.
• Öğrenci: Bireyin öğrenci olup olmadığını belirtir.
• bakiye: Bir bireyin taşıdığı ortalama bakiye.
• gelir: Bireyin geliri.

Belirli bir bireyin temerrüde düşme olasılığını tahmin eden bir lojistik regresyon modeli oluşturmak için öğrenci durumunu, banka bakiyesini ve geliri kullanacağız.

3. Adım: Eğitim ve test örnekleri oluşturun

Daha sonra veri setini, modeli eğitmek için bir eğitim setine ve modeli test etmek için bir test setine böleceğiz.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Adım 4: Lojistik regresyon modelini yerleştirin

Daha sonra, lojistik regresyon modelini veri kümesine sığdırmak için LogisticRegression() işlevini kullanacağız:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Adım 5: Model Tanılaması

Regresyon modelini yerleştirdikten sonra modelimizin test veri seti üzerindeki performansını analiz edebiliriz.

İlk olarak model için karışıklık matrisini oluşturacağız :

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

Karışıklık matrisinden şunu görebiliriz:

• #Doğru olumlu tahminler: 2886
• #Doğru olumsuz tahminler: 0
• #Yanlış pozitif tahminler: 113
• #Yanlış negatif tahminler: 1

Ayrıca model tarafından yapılan düzeltme tahminlerinin yüzdesini bize söyleyen doğruluk modelini de alabiliriz:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Bu bize modelin bir bireyin temerrüde düşüp düşmeyeceği konusunda %96,2 oranında doğru tahminde bulunduğunu gösteriyor.

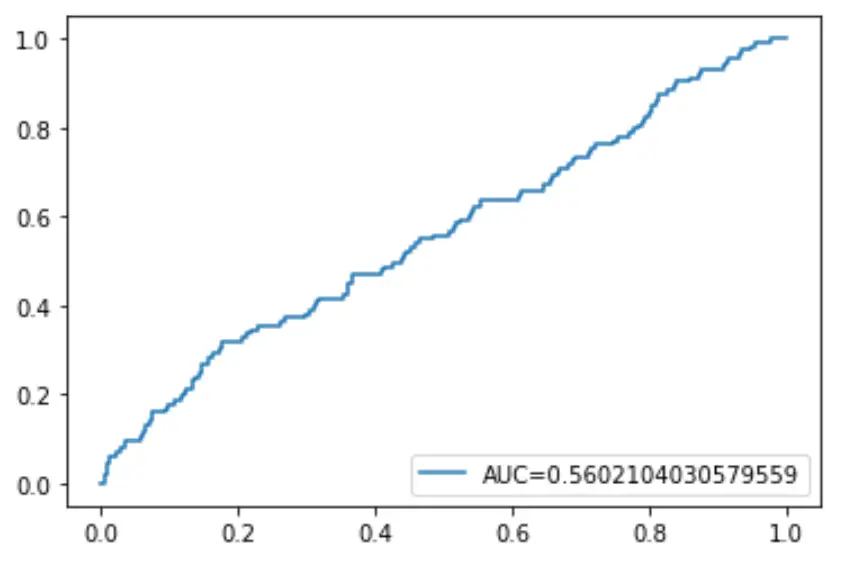
Son olarak, tahmin olasılığı eşiği 1’den 0’a düşürüldüğünde model tarafından tahmin edilen gerçek pozitiflerin yüzdesini görüntüleyen Alıcı Çalışma Karakteristiği (ROC) eğrisini çizebiliriz.

AUC (eğrinin altındaki alan) ne kadar yüksek olursa modelimiz sonuçları o kadar doğru tahmin edebilir:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()