Lorenz eğrisi

Bu makale Lorenz eğrisinin ne olduğunu ve ne için kullanıldığını açıklamaktadır. Bir popülasyonun Lorenz eğrisinin nasıl oluşturulacağını keşfedecek ve ayrıca alıştırmanın adım adım çözüldüğünü görebileceksiniz. Son olarak Lorenz eğrisinin özellikleri ve Gini indeksi ile ilişkisi sunulmaktadır.

Lorenz eğrisi nedir?

Lorenz eğrisi, bir bölgenin nüfusu arasındaki ekonomik eşitsizliklerin grafiksel temsilidir. Başka bir deyişle Lorenz eğrisi, bir bölge üzerindeki gelir dağılımındaki eşitsizlikleri analiz etmemizi sağlayan bir eğridir.

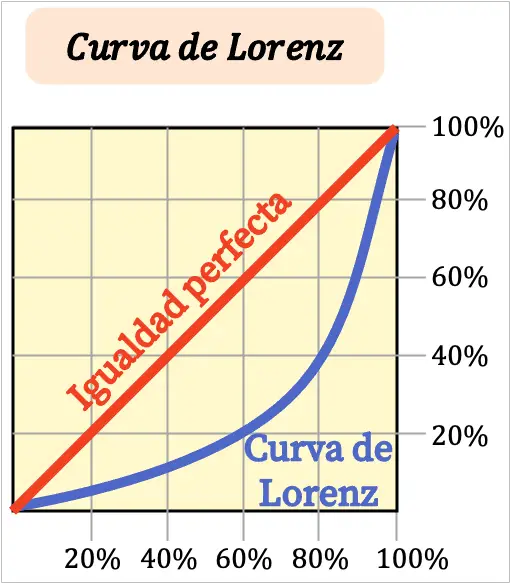
Lorenz eğrisi ne kadar düz olursa, bölgenin geliri de o kadar eşitlikçi olur. Öte yandan Lorenz eğrisi ne kadar kavisli olursa gelir de o kadar eşitsiz dağılır.

Tipik olarak Lorenz eğrisinin eksenleri yüzde olarak ifade edilir. Grafiğin X ekseni nüfus yüzdesini, Y ekseni ise gelir yüzdesini göstermektedir.

Lorenz eğrisi, 1905 yılında 20. yüzyılın çok önemli Amerikalı ekonomisti Max Otto Lorenz tarafından icat edildi.

Lorenz eğrisi nasıl hesaplanır

Lorenz eğrisinin tanımını öğrendikten sonra bu istatistiksel eğrinin nasıl hesaplandığını göreceğiz. Lorenz eğrisini tanımlamak için bir formül bulunduğunu ancak pratikte genellikle kullanılmadığını belirtmek gerekir. Bu yüzden nasıl yapıldığını görebilmeniz için bir örneği adım adım çözeceğiz.

• Geliri aşağıdaki tabloda sunulan nüfusun Lorenz eğrisini temsil eder:

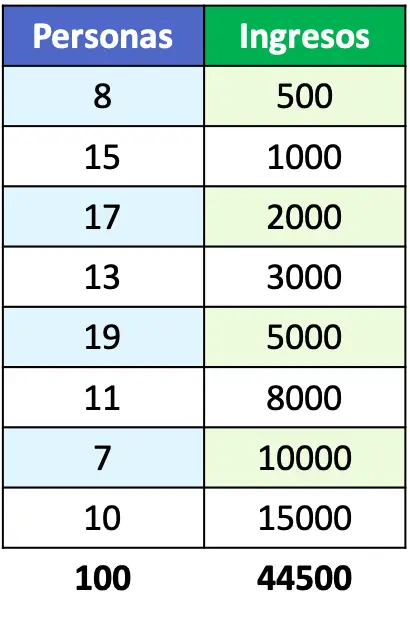
Eğer problem cümlesi bize Lorenz eğrisi fonksiyonunun örneğini vermiş olsaydı, fonksiyonu doğrudan bir grafik üzerinde temsil edebilirdik. Ancak bu durumda bize yalnızca nüfus gelirini veriyorlar, dolayısıyla her insan grubunun yüzdesini hesaplamamız gerekiyor.

Dolayısıyla kişi sayısı ve gelir yüzdelerini belirlemek için nüfus değişkenine ilişkin tabloya iki sütun eklemeliyiz:

• Birikmiş mutlak frekansı ( _Fi ) içeren bir sütun.
• Kümülatif mutlak frekansın toplam kişi sayısına bölünmesiyle hesaplanan kümülatif yüzdeye karşılık gelen ikinci bir sütun.

Öte yandan gelir değişkeni için üç sütun eklemeliyiz:

• Toplam gelirin hesaplandığı sütun, kişi sayısı ile her kişinin aldığı gelirin çarpımına eşittir.
• Toplam gelirin birikmiş mutlak frekansına ( _Fi ) sahip bir saniye.
• Bir önceki sütunun nüfusun toplam gelirine bölünmesiyle belirlenen birikmiş yüzdeyi içeren üçüncü sütun.

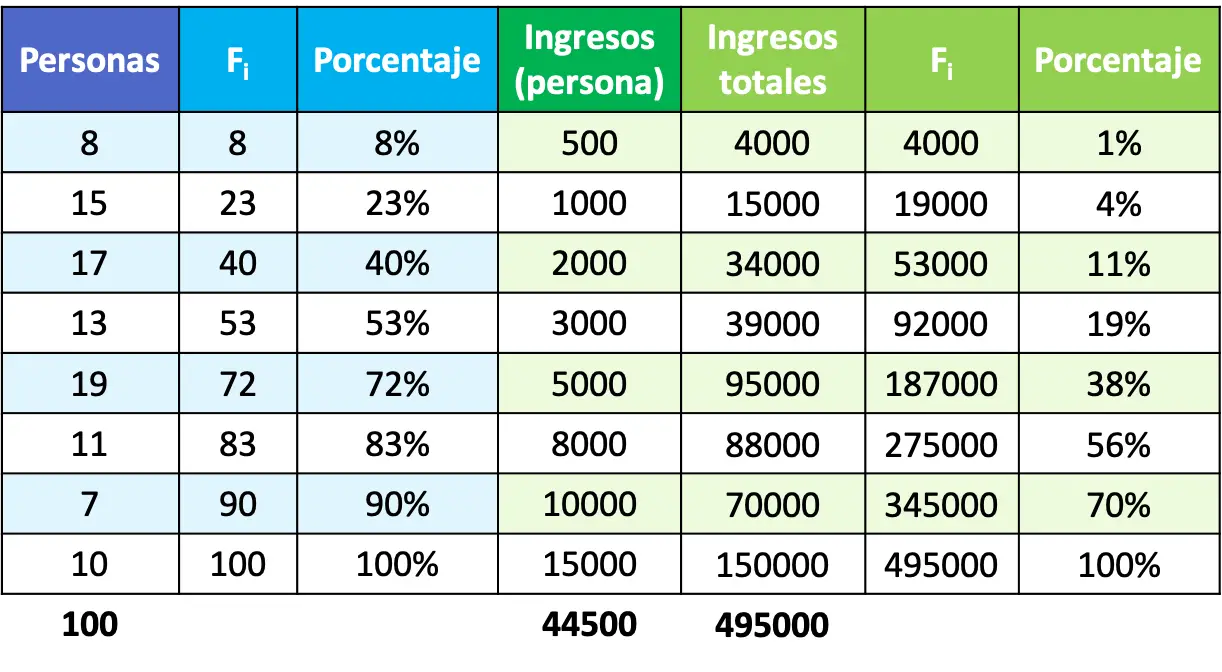
Son olarak artık yüzdeleri hesapladığımıza göre geriye kalan tek şey noktaları bir grafik üzerinde işaretleyip Lorenz eğrisini oluşturmak için bunları birleştirmek. X ekseninin nüfus yüzdesi, Y ekseninin ise gelir yüzdesi olduğunu unutmayın.

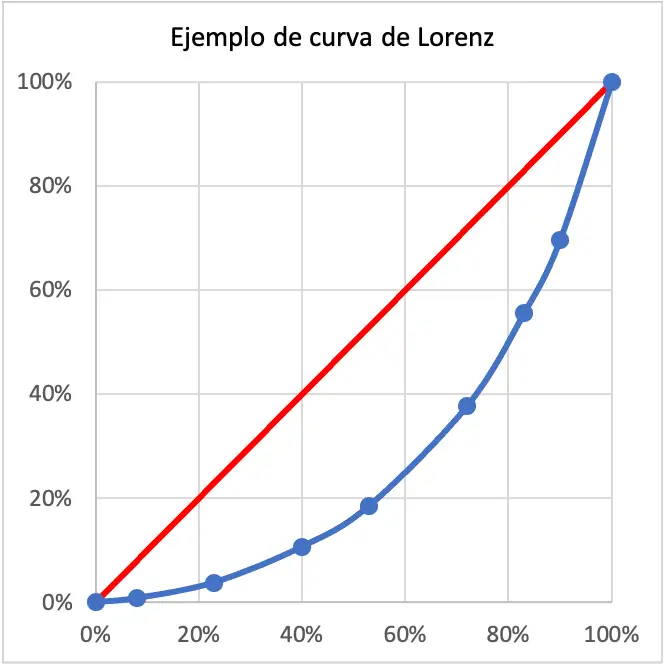
Bu durumda Lorenz eğrisi çok geniş olduğundan incelenen nüfusun geliri çok eşitsizdir. Aslında Lorenz eğrisi tam eşitliği temsil eden kırmızı çizgiden çok uzaktır.

Lorenz eğrisinin yorumlanması

Bu bölümde bir popülasyonun Lorenz eğrisinin nasıl yorumlanacağı açıklanmaktadır, çünkü bunun grafiğini nasıl çizeceğinizi bilmenin yanı sıra, bunun ne anlama geldiğini de anlamanız gerekir.

Lorenz eğrisi, nüfusun yüzde kaçının bir bölgenin toplam gelirinin yüzdesine sahip olduğunu gösterir. Örneğin yukarıda gösterilen Lorenz eğrisi örneğinde nüfusun %40’ının, tüm nüfus gelirinin %11’i kadar bir geliri vardır. Yani burası çok dengesiz bir bölge.

Dolayısıyla Lorenz eğrisi, bir ülke veya bölgenin sakinleri arasındaki gelir eşitliğini veya eşitsizliğini görsel olarak temsil eder . Tam eşitliği ifade eden çizgiden ne kadar uzaklaşılırsa, nüfusun gelirinin de o kadar eşitsiz olduğu anlamına gelir. Öte yandan Lorenz eğrisi sağa yaklaştıkça nüfusun gelirinin daha adil dağıtıldığı anlamına geliyor.

Ek olarak, grafik boyunca bir Lorenz eğrisi başka bir Lorenz eğrisinin üzerindeyse bu, birinci nüfusun gelirinin ikinci nüfusun gelirinden daha eşit olduğu anlamına gelir.

Lorenz eğrisi ve Gini katsayısı

Makale boyunca açıklandığı gibi Lorenz eğrisi, bir bölgenin gelirinin nasıl dağıtıldığını ve bir bölgenin ne kadar eşitsiz olduğunu grafiksel olarak gösterir.

Gini endeksi olarak da adlandırılan Gini katsayısı ise sayısal olarak bir bölgenin ekonomik eşitsizliğini gösterir.

Lorenz eğrisi ve Gini katsayısı bu nedenle bağlantılıdır. Aslında bir ülkenin Gini katsayısı Lorenz eğrisinden hesaplanabilir. Aşağıdaki makalede bunun nasıl yapılacağını görebilirsiniz:

Lorenz eğrisinin özellikleri

Lorenz eğrisi aşağıdaki özelliklere sahiptir:

• Lorenz eğrisi her zaman (0,0) noktasında başlar ve (100,100) noktasında biter.
• Örnek ortalaması sıfırsa Lorenz eğrisi tanımsızdır.
• Lorenz eğrisi grafikte mükemmel eşitlik çizgisinin üzerinde görünemez.
• Gelirin negatif olamayacağını varsayarsak Lorenz eğrisi her zaman artmaktadır.