Makine öğreniminde aşırı uyum nedir? (açıklama ve örnekler)

Makine öğreniminde, belirli olaylar hakkında doğru tahminlerde bulunabilmek için sıklıkla modeller oluştururuz.

Örneğin, yanıt değişkeninin lise öğrencilerine yönelik ACT puanını tahmin etmek için ders çalışmak için harcanan saat tahmin değişkenini kullanan bir regresyon modeli oluşturmak istediğimizi varsayalım.

Bu modeli oluşturmak için, belirli bir okul bölgesindeki yüzlerce öğrencinin ders çalışmak için harcadığı saatlere ve buna karşılık gelen ACT puanına ilişkin verileri toplayacağız.

Daha sonra bu verileri, belirli bir öğrencinin çalışılan toplam saat sayısına göre alacağı puan hakkında tahminlerde bulunabilecek bir model geliştirmek için kullanacağız.

Modelin kullanışlılığını değerlendirmek için modelin tahminlerinin gözlemlenen verilerle ne kadar iyi eşleştiğini ölçebiliriz. Bunu yapmak için en yaygın kullanılan ölçümlerden biri, aşağıdaki şekilde hesaplanan ortalama kare hatasıdır (MSE):

MSE = (1/n)*Σ(y _ben – f(x _ben )) ²

Altın:

• n: toplam gözlem sayısı
• y _i : ^i’inci gözlemin yanıt değeri
• f(x _i ): ^i’inci gözlemin tahmin edilen tepki değeri

Model tahminleri gözlemlere ne kadar yakınsa MSE o kadar düşük olacaktır.

Ancak makine öğreniminde yapılan en büyük hatalardan biri, eğitim MSE’sini , yani model tahminlerinin, modeli eğitmek için kullandığımız verilerle ne kadar iyi eşleştiğini azaltmak için modelleri optimize etmektir.

Bir model, eğitim MSE’sini azaltmaya çok fazla odaklandığında, genellikle eğitim verilerinde şans eseri oluşan kalıpları bulmak için çok fazla çaba harcar. Daha sonra model görünmeyen verilere uygulandığında performansı zayıflar.

Bu olay aşırı uyum olarak bilinir. Bu, bir modeli eğitim verilerine çok yakın “uydurduğumuzda” ve dolayısıyla yeni veriler üzerinde tahminler yapmak için kullanışlı olmayan bir model oluşturduğumuzda meydana gelir.

Aşırı uyum örneği

Aşırı uyumu anlamak için, ACT puanını tahmin etmek amacıyla çalışmaya harcanan saatleri kullanan bir regresyon modeli oluşturma örneğine dönelim.

Belirli bir okul bölgesindeki 100 öğrenci için veri topladığımızı ve iki değişken arasındaki ilişkiyi görselleştirmek için hızlı bir dağılım grafiği oluşturduğumuzu varsayalım:

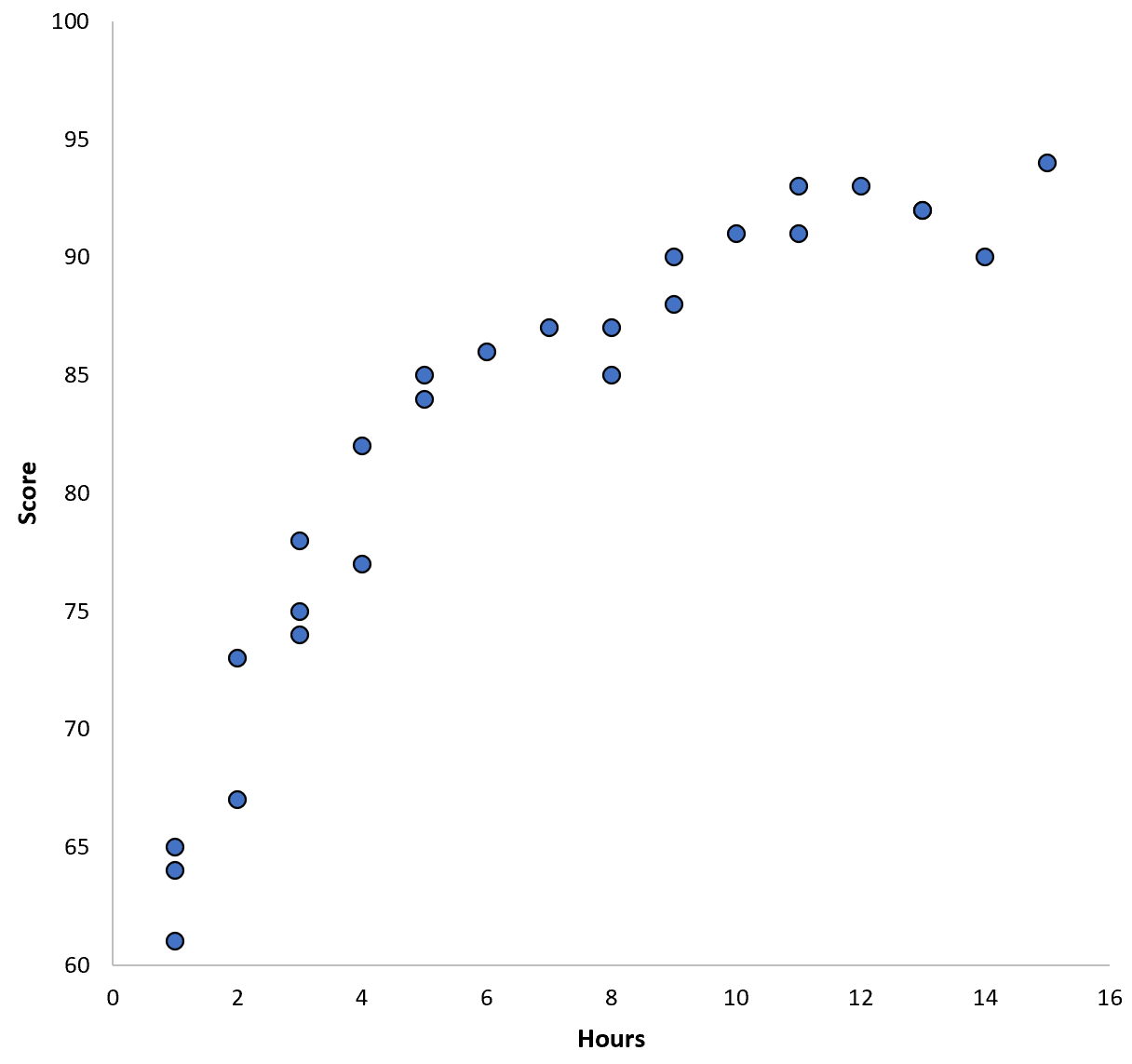
İki değişken arasındaki ilişki ikinci dereceden görünüyor, dolayısıyla aşağıdaki ikinci dereceden regresyon modelini uyguladığımızı varsayalım:

Puan = 60,1 + 5,4*(Saat) – 0,2*(Saat) ²

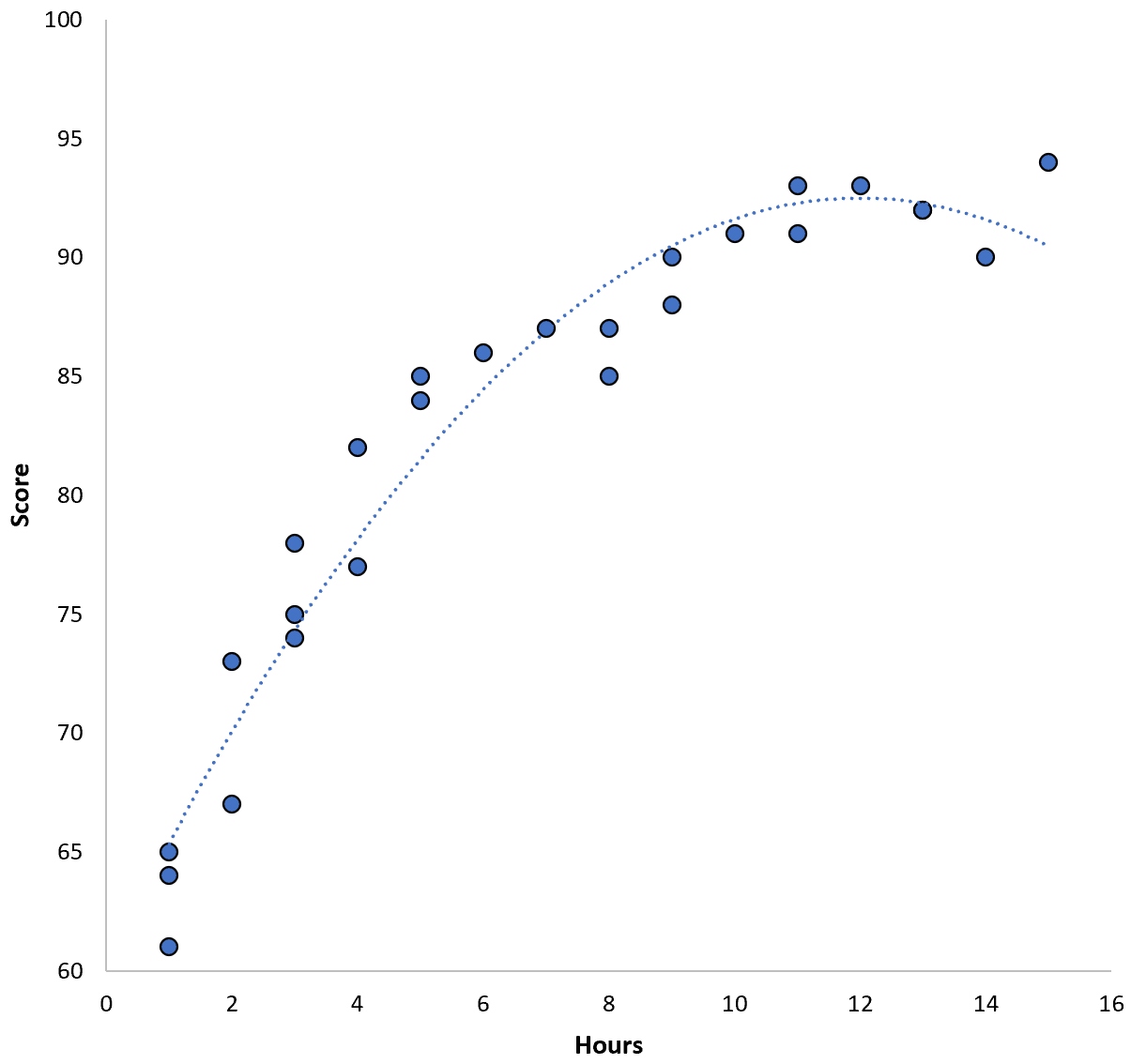
Bu modelin eğitim ortalama kare hatası (MSE) 3,45’tir . Yani modelin yaptığı tahminler ile gerçek ACT puanları arasındaki karekök ortalama farkı 3,45’tir.

Ancak daha yüksek dereceli bir polinom modeli uydurarak bu eğitim MSE’sini azaltabiliriz. Örneğin aşağıdaki modeli uyguladığımızı varsayalım:

Puan = 64,3 – 7,1*(Saat) + 8,1*(Saat) ² – 2,1*(Saat) ³ + 0,2*(Saat ^{) 4 – 0,1*(Saat) 5 +} 0,2(Saat) ⁶

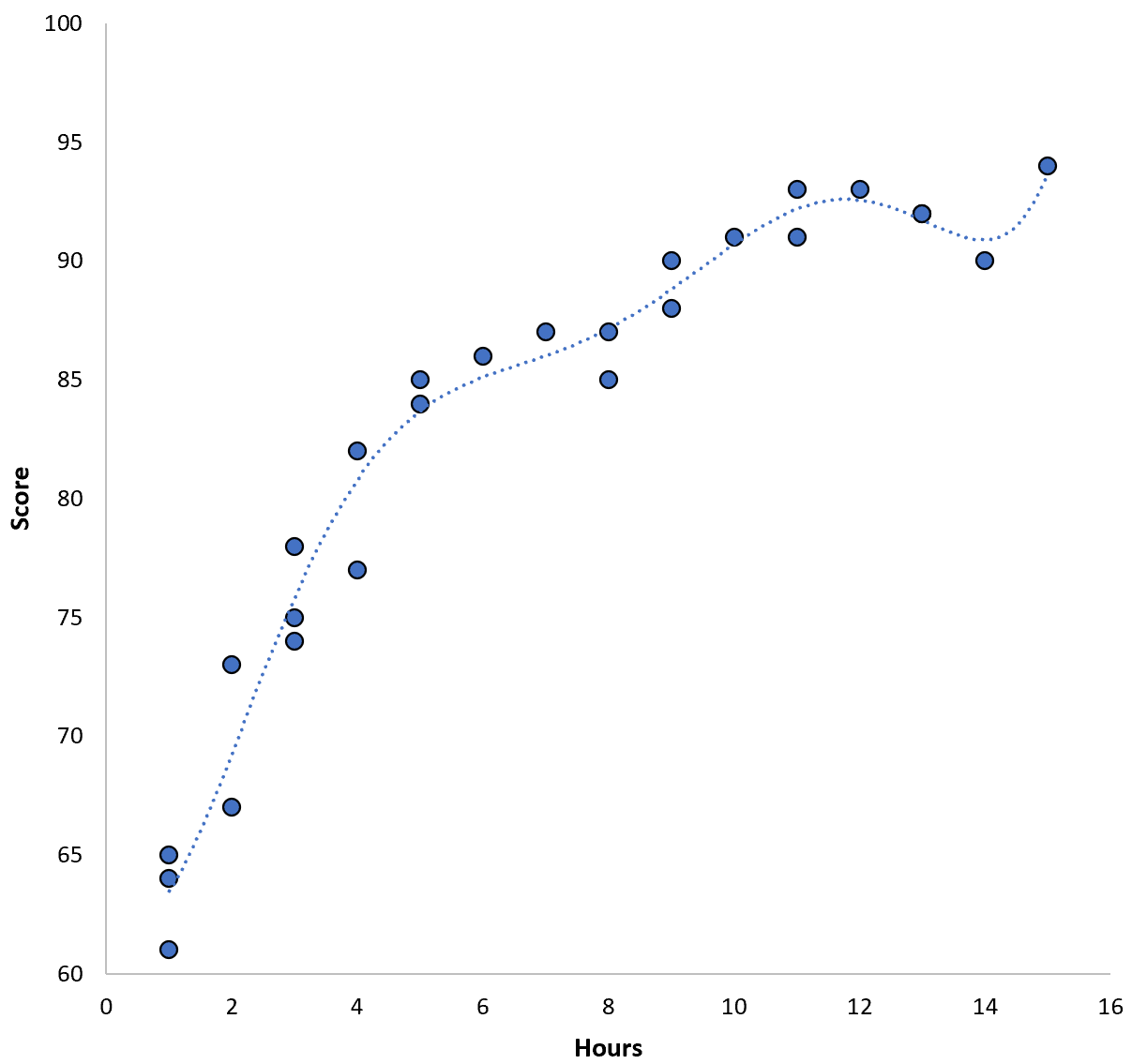
Regresyon çizgisinin gerçek verilere nasıl önceki regresyon çizgisine göre çok daha yakın uyduğuna dikkat edin.

Bu modelin eğitim kök ortalama kare hatası (MSE) yalnızca 0,89’dur . Yani modelin yaptığı tahminler ile gerçek ACT puanları arasındaki karekök ortalama farkı 0,89’dur.

Bu MSE eğitimi önceki modelin ürettiğinden çok daha küçüktür.

Ancak MSE eğitimiyle , yani modelin tahminlerinin, modeli eğitmek için kullandığımız verilerle ne kadar iyi eşleştiğiyle pek ilgilenmiyoruz. Bunun yerine, esas olarak MSE testini , yani modelimizin görünmeyen verilere uygulandığı MSE’yi önemsiyoruz.

Yukarıdaki yüksek dereceli polinom regresyon modelini görünmeyen bir veri kümesine uygularsak, muhtemelen daha basit ikinci dereceden regresyon modelinden daha kötü performans gösterir. Yani daha yüksek bir MSE testi üretecektir ki bu da tam olarak istemediğimiz bir durumdur.

Aşırı uyum nasıl tespit edilir ve önlenir

Aşırı uyumu tespit etmenin en basit yolu çapraz doğrulama yapmaktır. En sık kullanılan yöntem k-katlı çapraz doğrulama olarak bilinir ve şu şekilde çalışır:

Adım 1: Bir veri kümesini rastgele olarak yaklaşık olarak eşit büyüklükte k gruba veya “katlamaya” bölün.

Adım 2: Tutma setiniz olarak kıvrımlardan birini seçin. Şablonu kalan k-1 kıvrımlarına göre ayarlayın. Gerilmiş kattaki gözlemler üzerinden MSE testini hesaplayın.

Adım 3: Her seferinde dışlama kümesi olarak farklı bir küme kullanarak bu işlemi k kez tekrarlayın.

Adım 4: Testin k MSE’lerinin ortalaması olarak testin genel MSE’sini hesaplayın.

MSE testi = (1/k)*ΣMSE _i

Altın:

• k: Katlama sayısı
• MSE _i : MSE’yi ^i’inci yinelemede test edin

Bu MSE testi bize belirli bir modelin bilinmeyen veriler üzerinde nasıl performans göstereceğine dair iyi bir fikir verir.

Uygulamada, birkaç farklı model yerleştirebilir ve MSE testini bulmak için her model üzerinde k-katlı çapraz doğrulama gerçekleştirebiliriz. Daha sonra, gelecekte tahminlerde bulunmak için kullanılacak en iyi model olarak en düşük MSE testine sahip modeli seçebiliriz.

Bu, eğitim MSE’sini en aza indiren ve geçmiş verilere iyi “uyan” bir modelin aksine, gelecekteki verilerde en iyi performansı göstermesi muhtemel bir modeli seçmemizi sağlar.

Ek kaynaklar

Makine öğreniminde önyargı-varyans değişimi nedir?
K-Fold Çapraz Doğrulamaya Giriş
Makine öğrenmesinde regresyon ve sınıflandırma modelleri