Mann-whitney u testi
Örnek dağılımları normal dağılmadığında ve örnek boyutları küçük olduğunda (n < 30) iki bağımsız örnek arasındaki farkları karşılaştırmak için bir Mann-Whitney U testi (bazen Wilcoxon sıralama toplamı testi olarak da adlandırılır) kullanılır.
Bağımsız iki örnekli t testinin parametrik olmayan eşdeğeri olarak kabul edilir.
Mann-Whitney U testini ne zaman kullanabileceğinize dair bazı örnekler:
- A üniversitesinden beş mezunun maaşlarını B üniversitesinden beş mezunun maaşlarıyla karşılaştırmak istiyorsunuz. Maaşlar normal dağılmıyor.
- Kilo kaybının iki grup için değişip değişmediğini bilmek istiyorsunuz: A diyetini kullanan 12 kişi ve B diyetini kullanan 10 kişi. Kilo kaybı normal şekilde dağılmıyor.
- A sınıfındaki 8 öğrencinin puanlarının B sınıfındaki 7 öğrencinin puanlarından farklı olup olmadığını bilmek istiyorsunuz. Puanlar normal dağılmıyor.
Her örnekte iki grubu karşılaştırmak istiyorsunuz; örnekleme dağılımları normal değil ve örneklem boyutları küçük.
Bu nedenle aşağıdaki varsayımlar karşılandığı sürece Mann-Whitney U testi uygundur.
Mann-Whitney U Testi Varsayımları
Mann-Whitney U testini gerçekleştirmeden önce aşağıdaki dört varsayımın karşılandığından emin olmalısınız:
- Sıradan veya sürekli: Analiz ettiğiniz değişken sıralı veya süreklidir. Sıralı değişkenlerin örnekleri arasında Likert maddeleri (örneğin, “kesinlikle katılmıyorum” ile “kesinlikle katılıyorum” arasında değişen 5 puanlık bir ölçek) yer alır. Sürekli değişkenlerin örnekleri arasında boy (inç olarak ölçülür), ağırlık (pound olarak ölçülür) veya test puanları (0 ile 100 arasında ölçülür) yer alır.
- Bağımsızlık: Her iki grubun tüm gözlemleri birbirinden bağımsızdır.
- Şekil: Her iki grubun dağılım şekilleri yaklaşık olarak aynıdır.
Bu varsayımlar karşılanırsa Mann-Whitney U testi yapılabilir.
Mann-Whitney U Testi Nasıl Yapılır?
Mann-Whitney U testini gerçekleştirmek için standart beş adımlı hipotez testi prosedürünü takip ediyoruz:
1. Varsayımları belirtin.
Çoğu durumda Mann-Whitney U testi iki kuyruklu bir test olarak gerçekleştirilir. Boş ve alternatif hipotezler şu şekilde yazılmıştır:
H 0 : İki popülasyon eşittir
H a : İki popülasyon eşit değil
2. Hipotez için kullanılacak bir önem düzeyi belirleyin.
Bir önem düzeyine karar verin. Ortak seçenekler 0,01, 0,05 ve 0,1’dir.
3. Test istatistiğini bulun.
Test istatistiği U ile gösterilir ve aşağıda tanımlandığı gibi U 1 ve U 2’den küçüktür:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
burada n1 ve n2 sırasıyla numune 1 ve 2’nin numune boyutlarıdır ve R1 ve R2 sırasıyla numune 1 ve 2’nin sıralarının toplamıdır.
Aşağıdaki örnekler bu test istatistiğinin nasıl bulunacağını ayrıntılı olarak gösterecektir.
4. Sıfır hipotezini reddedin veya reddetmeyin.
Test istatistiklerini kullanarak, Mann-Whitney U tablosunda bulunan anlamlılık düzeyi ve kritik değere dayalı olarak sıfır hipotezini reddedip reddedemeyeceğinizi belirleyin.
5. Sonuçları yorumlayın.
Test sonuçlarını sorulan soru bağlamında yorumlayın.
Mann-Whitney U testi gerçekleştirme örnekleri
Aşağıdaki örnekler Mann-Whitney U testinin nasıl gerçekleştirileceğini göstermektedir.
örnek 1
Yeni bir ilacın panik atağı önlemede etkili olup olmadığını bilmek istiyoruz. Toplam 12 hasta rastgele 6 kişilik iki gruba bölünüyor ve yeni ilacı veya plaseboyu almak üzere görevlendiriliyor. Hastalar daha sonra bir ay boyunca yaşadıkları panik atak sayısını kaydederler.
Sonuçlar aşağıda gösterilmektedir:
| YENİ İLAÇ | PLASEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Yeni ilaç grubuyla karşılaştırıldığında plasebo grubundaki hastalar arasında panik atak sayısında bir fark olup olmadığını görmek için Mann-Whitney U testi yapın. 0,05 anlamlılık düzeyini kullanın.
1. Varsayımları belirtin.
H 0 : İki popülasyon eşittir
H a : İki popülasyon eşit değil
2. Hipotez için kullanılacak bir önem düzeyi belirleyin.
Sorun bize 0,05 anlamlılık düzeyini kullanmamız gerektiğini söylüyor.
3. Test istatistiğini bulun.
Test istatistiğinin U olarak gösterildiğini ve aşağıda tanımlandığı gibi U 1 ve U 2’den daha küçük olduğunu hatırlayın:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
burada n1 ve n2 sırasıyla numune 1 ve 2’nin numune boyutlarıdır ve R1 ve R2 sırasıyla numune 1 ve 2’nin sıralarının toplamıdır.
R1 ve R2’yi bulmak için her iki gruptan gözlemleri birleştirmemiz ve bunları küçükten büyüğe doğru sıralamamız gerekir:
| YENİ İLAÇ | PLASEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Toplam örnek: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Sıralar: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = örnek 1 için sıraların toplamı = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = örnek 2 için sıraların toplamı = 1,5+3+6,5+10+11+12 = 44
Daha sonra, U 1 ve U 2’yi bulmak için örnek büyüklüklerimizi n 1 ve n 2’nin yanı sıra sıra toplamımız R 1 ve R 2’yi kullanırız.
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Test istatistiklerimiz U1 ve U2’den küçük olanıdır ve U=13 olur.
Not: U = 13’ü belirlemek için Mann-Whitney U testi hesaplayıcısını da kullanabiliriz.
4. Sıfır hipotezini reddedin veya reddetmeyin.
Mann-Whitney U tablosu, n 1 = 6 ve n 2 = 6’yı 0,05 anlamlılık düzeyinde kullanarak kritik değerin 5 olduğunu söyler:
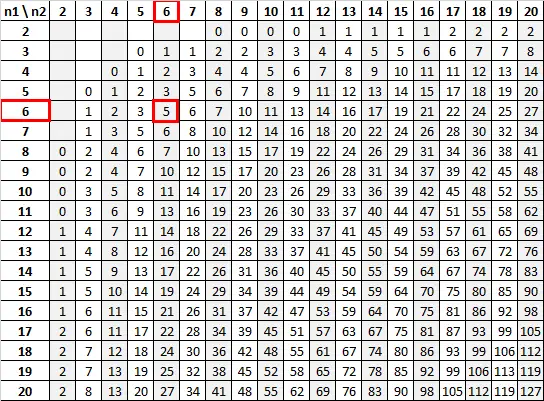
Test istatistiğimiz (13) kritik değerimizden (5) büyük olduğundan sıfır hipotezini reddedemiyoruz.
5. Sonuçları yorumlayın.
Sıfır hipotezini reddetmeyi başaramadığımız için, plasebo grubundaki hastaların yaşadığı panik atak sayısının yeni ilaç grubundakilerden farklı olduğunu söyleyecek yeterli kanıtımız yok.
Örnek 2
Bir hafta boyunca günde 30 dakika çalışmanın öğrencilerin sınavda daha iyi performans göstermelerine yardımcı olup olmadığını bilmek istiyoruz. Toplam 15 hasta rastgele çalışma grubuna veya çalışma grubuna atanmadı. Bir hafta sonra tüm öğrenciler aynı sınava girer.
Her iki gruba ait test sonuçları aşağıda gösterilmiştir:
| ÇALIŞMAK | ÇALIŞMAK YOK |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Çalışmayan gruba kıyasla çalışma grubunun test puanlarında bir fark olup olmadığını görmek için Mann-Whitney U testi yapın. 0,01 anlamlılık düzeyini kullanın.
1. Varsayımları belirtin.
H 0 : İki popülasyon eşittir
H a : İki popülasyon eşit değil
2. Hipotez için kullanılacak bir önem düzeyi belirleyin.
Sorun bize 0,01 anlamlılık düzeyini kullanmamız gerektiğini söylüyor.
3. Test istatistiğini bulun.
Test istatistiğinin U olarak gösterildiğini ve aşağıda tanımlandığı gibi U 1 ve U 2’den daha küçük olduğunu hatırlayın:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
burada n1 ve n2 sırasıyla numune 1 ve 2’nin numune boyutlarıdır ve R1 ve R2 sırasıyla numune 1 ve 2’nin sıralarının toplamıdır.
R1 ve R2’yi bulmak için her iki gruptan gözlemleri birleştirmemiz ve bunları küçükten büyüğe doğru sıralamamız gerekir:
| ÇALIŞMAK | ÇALIŞMAK YOK |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Toplam örnek: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Satırlar: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = örnek 1 için sıraların toplamı = 5+7+8+9+10+12+14+15 = 80
R 2 = örnek 2 için sıraların toplamı = 1+2+3+4+6+11+13 = 40
Daha sonra, U 1 ve U 2’yi bulmak için örnek büyüklüklerimizi n 1 ve n 2’nin yanı sıra sıra toplamımız R 1 ve R 2’yi kullanırız.
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Test istatistiklerimiz U1 ve U2’den küçük olanıdır ve U=12 olur.
Not: U = 12 olduğunu belirlemek için Mann-Whitney U testi hesaplayıcısını da kullanabiliriz.
4. Sıfır hipotezini reddedin veya reddetmeyin.
n 1 = 8 ve n 2 = 7’yi 0,01 anlamlılık düzeyinde kullanarak Mann-Whitney U tablosu bize kritik değerin 6 olduğunu söyler:
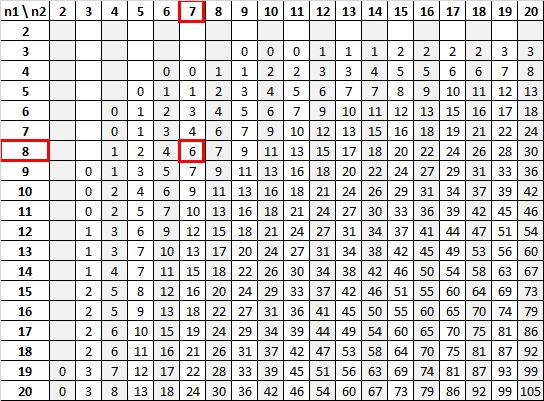
Test istatistiğimiz (12) kritik değerimizden (6) büyük olduğundan sıfır hipotezini reddedemiyoruz.
5. Sonuçları yorumlayın.
Sıfır hipotezini reddetmeyi başaramadığımız için, ders çalışan öğrencilerin test puanlarının çalışmayan öğrencilerin test puanlarından farklı olduğunu söyleyecek yeterli kanıtımız yok.
Ek kaynaklar
Mann-Whitney U Testi Hesaplayıcı
Mann-Whitney U Masası
Excel’de Mann-Whitney U Testi Nasıl Yapılır
R’de Mann-Whitney U testi nasıl yapılır?
Python’da Mann-Whitney U Testi Nasıl Yapılır?
SPSS’de Mann-Whitney U Testi Nasıl Yapılır?
Stata’da Mann-Whitney U testi nasıl yapılır?
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil