Medyan
Bu makalede, bir veri kümesinin medyanının ne olduğu ve gruplanmamış veriler ve gruplandırılmış veriler için medyanın nasıl bulunacağı açıklanmaktadır. Ek olarak, sondaki çevrimiçi hesap makinesini kullanarak herhangi bir veri serisinin medyanını hesaplayabilirsiniz.
Medyan nedir?
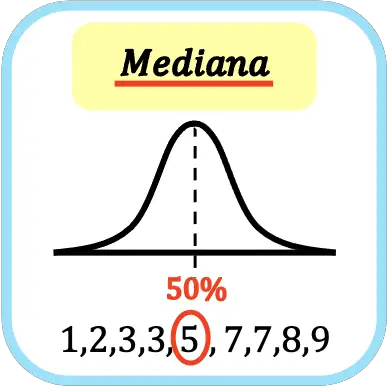
İstatistiklerde medyan , en küçükten en büyüğe doğru sıralanan tüm verilerin ortadaki değeridir. Başka bir deyişle medyan sıralı veri setini iki eşit parçaya böler.
Medyan, bir olasılık dağılımını tanımlamak için kullanılan merkezi konum ölçüsüdür.
👉Herhangi bir veri setinin medyanını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.
Genel olarak Self terimi sıklıkla ortanın sembolü olarak kullanılır.
Diğer merkezi konum ölçüleri ortalama ve moddur; aşağıda aralarındaki farkları göreceğiz. Benzer şekilde, merkezi olmayan konum ölçüleri çeyrekler, beşte birlikler, ondalıklar, yüzdelikler vb.’dir.
Bir veri setinin medyanının ikinci çeyrek, beşinci ondalık dilim ve 50. yüzdelik dilime denk geldiğine dikkat edilmelidir.
Medyan nasıl hesaplanır
Medyanın hesaplanması, toplam veri sayısının çift veya tek olmasına bağlıdır:
- Toplam veri sayısı tek ise medyan verinin tam ortasında kalan değer olacaktır. Yani sıralanan verinin (n+1)/2 konumundaki değeri.
- Toplam veri noktası sayısı çift ise medyan, merkezde bulunan iki veri noktasının ortalaması olacaktır. Yani sıralı verinin n/2 ve n/2+1 konumlarında bulunan değerlerin aritmetik ortalamasıdır .
![]()
![]()
Altın
![]()
örnekteki veri öğelerinin toplam sayısıdır.
Medyan hesaplama örnekleri
Medyanın nasıl hesaplandığını görebilmeniz için aşağıda her durum için bir tane olmak üzere iki gerçek dünya örneği verilmiştir. Öncelikle tek veri setinin medyanı hesaplanacak, daha sonra çift veri setinin medyanı hesaplanacaktır.
Tek verilerin medyanı
- Aşağıdaki verilerin medyanını hesaplayın: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5
Hesaplama yapmadan önce yapmamız gereken ilk şey verileri sıralamak yani sayıları küçükten büyüğe doğru sıralamaktır.
![]()
Bu durumda 11 gözlemimiz var, yani toplam veri sayısı tektir. Bu nedenle medyanın konumunu hesaplamak için aşağıdaki formülü uygularız:
![]()
Bu nedenle medyan altıncı konumda yer alan veri olacaktır ve bu durumda bu değer 4’e karşılık gelir.
![]()
çift verinin medyanı
- Aşağıdaki gözlemlerin medyanı nedir? 2, 6, 2, 8, 9, 4, 7, 11, 4, 13
Medyanı elde etmek için öncelikle tüm verileri artan düzende sıralamanız gerekir:
![]()
Bu örnek öncekinden farklı çünkü bu kez elimizde toplam 10 gözlem var, bu da çift sayı. Bu nedenle ortalamayı belirleme prosedürü biraz daha karmaşıktır.
Öncelikle ortancanın bulunacağı iki merkezi konumu hesaplamanız gerekir, bunun için aşağıdaki iki formülü uygulamanız gerekir:
![]()
![]()
Bu nedenle medyan, sırasıyla 6 ve 7 değerlerine karşılık gelen beşinci ve altıncı konum arasında olacaktır. Somut olarak medyan, söz konusu değerlerin aritmetik ortalaması olacaktır:
![]()
medyan hesaplayıcı
Medyanını hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Gruplandırılmış veriler için medyan
Veriler aralıklar halinde gruplandırıldığında medyanı hesaplamak için öncelikle aşağıdaki formülü kullanarak medyanın düştüğü aralığı veya bölmeyi bulmanız gerekir:
![]()
Böylece medyan, kümülatif mutlak frekansı önceki cebirsel ifadeyle elde edilen sayıdan hemen büyük olan aralıkta olacaktır.
Medyanın ait olduğu aralığı bildiğimizde, medyanın tam değerini bulmak için aşağıdaki formülü uygulamamız gerekir:

Altın:
- L i medyanın bulunduğu aralığın alt sınırıdır.
- n , toplam gözlem sayısıdır.
- F i-1 önceki aralığın birikmiş mutlak frekansıdır.
- f i medyanın bulunduğu aralığın mutlak frekansıdır.
- I i orta aralığın genişliğidir.
Örnek olarak aşağıda, aralıklara göre gruplandırılmış verilerin medyanının hesaplandığı bir alıştırmayı çözdünüz.

Veri setinin medyanını bulmak için öncelikle hangi aralığa düştüğünü belirlememiz gerekir. Bunu yapmak için aşağıdaki formülü kullanıyoruz:
![]()
Yani medyan, kümülatif mutlak frekansı 15,5’ten hemen büyük olan aralıkta olacaktır; bu durumda bu, kümülatif mutlak frekansı 26 olan aralıktır [60,70). Ve medyan aralığını bildiğimizde, denklemin ikinci formülünü uygularız. işlem:


Sonuçta, havuzlanmış veri setinin medyanı 60,45’tir. Gördüğünüz gibi bu tür problemlerde medyan genellikle ondalık bir sayıdır.
medyan, ortalama ve mod
Bu son bölümde medyan, ortalama ve mod arasındaki farkın ne olduğunu göreceğiz. Bunlar merkezi konumun üç istatistiksel ölçüsüdür ancak anlamları farklıdır.
Görüldüğü gibi medyan, veriler sıralandığında merkezi konumda yer alan değer olarak tanımlanmaktadır.
Buna karşılık ortalama, tüm istatistiksel verilerin ortalama değeridir. Ortalamayı hesaplamak için tüm verileri toplamanız ve ardından sonucu veri noktalarının sayısına bölmeniz gerekir.
Son olarak mod, bir veri serisinde en çok tekrarlanan değerdir.
Gördüğünüz gibi, her üç istatistiksel ölçüm de bir olasılık dağılımını tanımlamaya yardımcı oluyor çünkü merkezi değerleri hakkında fikir veriyorlar. Ancak hiçbir ölçü diğerinden daha iyi değildir, sadece farklı kavramlara atıfta bulunurlar.