Medyan istatistikte neden önemlidir?

Medyan , tüm değerler en küçükten en büyüğe sıralandığında bir veri kümesinin ortadaki değerini temsil eder.

Örneğin aşağıdaki veri setindeki medyan 19’dur:

Veri kümesi: 3, 4, 11, 15, 19 , 22, 23, 23, 26

Medyan aynı zamanda bir veri setinin ^50. yüzdelik dilimini de temsil eder. Yani veri setindeki değerlerin tam yarısı medyanın üstünde, yarısı da medyanın altında.

Medyan, hesaplanması gereken önemli bir ölçümdür çünkü bize bir veri kümesinin “merkezinin” nerede olduğuna dair bir fikir verir. Bu aynı zamanda bize belirli bir veri setindeki “tipik” değer hakkında da fikir verir.

Örneğin belli bir şehirdeki 10.000 farklı evin satış fiyatlarını içeren bir veri setimiz olduğunu varsayalım.

Satır satır ham verilere bakmak yerine, o şehirdeki evlerin ortalama satış fiyatını hızlı bir şekilde anlamak için medyan değeri hesaplayabiliriz.

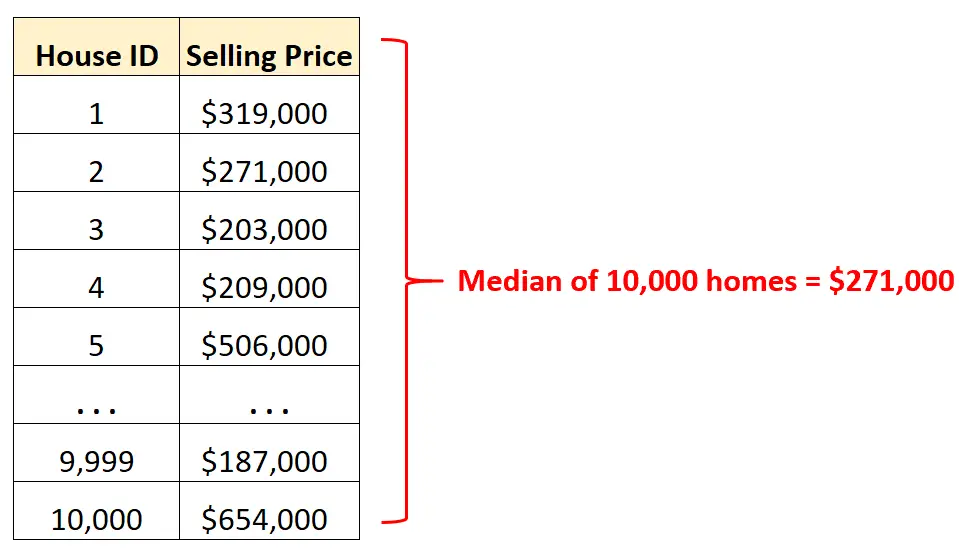
Ortalama satış fiyatının 271.000$ olduğunu bildiğimizde, 10.000 konutun tam yarısının bu tutarın üzerinde, diğer yarısının ise daha az fiyata satıldığını biliyoruz.

Bu aynı zamanda bize bu şehirdeki evlerin “tipik” satış fiyatı hakkında da fikir veriyor.

Medyan ne zaman kullanılır?

Veri setlerini analiz ederken genellikle merkezi değerin nerede olduğunu anlamak isteriz.

İstatistikte bir veri kümesinin merkezini ölçmek için kullandığımız iki ortak ölçüm vardır:

• Ortalama : Bir veri kümesindeki ortalama değer
• Medyan : Bir veri kümesindeki medyan değeri

Medyanın aşağıdaki durumlarda daha kullanışlı bir ölçü olduğu ortaya çıktı:

• Dağıtım asimetrik olduğunda.
• Dağıtım aykırı değerler içerdiğinde.

Bunu açıklamak için aşağıdaki iki örneği inceleyin.

Örnek 1: Çarpık bir dağılımın medyanının hesaplanması

Belirli bir şehrin sakinleri için aşağıdaki maaş dağılımını düşünün:

Medyan, bir sakinin “tipik” maaşını ortalamadan daha iyi yansıtıyor çünkü dağılım sağa çarpık.

Bu, dağılımın sağ tarafındaki yüksek ücretlerin ortalamayı dağılımın merkezinden uzaklaştırdığı anlamına gelir.

Bu özel örnekte ortalama maaş 47.000 Dolar, ortalama maaş ise 32.000 Dolardır. Medyan bu şehirdeki tipik maaşı çok daha iyi temsil ediyor.

Örnek 2: Aykırı değerlerin varlığında medyanın hesaplanması

Belirli bir caddedeki evlerin metrekarelerini gösteren aşağıdaki grafiği düşünün:

Ortalama, birkaç aşırı büyük evden büyük ölçüde etkilenirken, medyan etkilenmemektedir.

Ortancanın o sokaktaki bir evin “tipik” metrekaresini ortalamadan daha iyi yakaladığını görebiliriz çünkü aykırı değerlerden etkilenmez.

Özet

Bu makalede ele alınan ana noktaların kısa bir özetini burada bulabilirsiniz:

• Medyan, bir veri setindeki ortadaki değeri temsil eder.
• Medyan önemlidir çünkü bize bir veri setinde merkezi değerin nerede olduğuna dair bir fikir verir.
• Bir dağılım çarpık olduğunda ve/veya aykırı değerlere sahip olduğunda medyanın hesaplanması ortalamadan daha yararlı olma eğilimindedir.

Ek kaynaklar

Somut Örnekler: Ortalama, Medyan ve Modu Kullanma
Ortalama vs Ne Zaman Kullanılır? Medyan: Örneklerle
İstatistiklerde mod neden önemlidir?