Merkezi eğilim ölçüleri: tanım ve örnekler
Merkezi eğilim ölçüsü, bir veri kümesinin merkezi noktasını temsil eden tek bir değerdir. Bu değer aynı zamanda bir veri setinin “merkezi konumu” olarak da adlandırılabilir.
İstatistikte merkezi eğilimin üç yaygın ölçüsü vardır:
- Ortalama
- medyan
- Moda
Bu önlemlerin her biri, farklı yöntemler kullanarak bir veri kümesinin merkezi konumunu bulur. Analiz ettiğiniz veri türüne bağlı olarak diğer ikisi yerine bu üç ölçümden birini kullanmak daha iyi olabilir.
Bu makalede, merkezi eğilim ölçüsünün her birinin nasıl hesaplanacağına ve verilerinize dayanarak hangi ölçünün en iyi şekilde kullanılacağına nasıl karar vereceğinize bakacağız.
Merkezi eğilim ölçüleri neden faydalıdır?
Ortalamanın, medyanın ve modun nasıl hesaplanacağına bakmadan önce, bu ölçümlerin aslında neden yararlı olduğunu anlamak faydalı olacaktır.
Aşağıdaki senaryoyu düşünün:
Genç bir çift, yeni bir şehirde ilk evlerini nereden satın alacaklarına karar vermeye çalışmaktadır ve harcayabilecekleri en fazla miktar 150.000 dolardır. Şehrin bazı bölgelerinde pahalı evler, bazılarında ucuz evler, bazılarında ise orta fiyatlı evler bulunuyor. Aramalarını kolayca bütçelerine uygun belirli mahallelere daraltmak istiyorlar.
Çift, her mahalledeki müstakil evlerin fiyatlarına baksaydı, hangi mahallelerin bütçelerine en uygun olduğunu belirlemekte zorluk yaşayabilirler çünkü şöyle bir şey görebilirler:
Mahalle A ev fiyatları: 140.000 $, 190.000 $, 265.000 $, 115.000 $, 270.000 $, 240.000 $, 250.000 $, 180.000 $, 160.000 $, 200.000 $, 240.000 $, 280.000 $,…
B Mahallesi ev fiyatları: 140.000 $, 290.000 $, 155.000 $, 165.000 $, 280.000 $, 220.000 $, 155.000 $, 185.000 $, 160.000 $, 200.000 $, 190.000 $, 140.000 $, 145,0 $ 0 0,…
C Mahallesi ev fiyatları: 140.000 $, 130.000 $, 165.000 $, 115.000 $, 170.000 $, 100.000 $, 150.000 $, 180.000 $, 190.000 $, 120.000 $, 110.000 $, 130.000 $, 120,0 $ 0 0,…
Bununla birlikte, eğer her mahalledeki evlerin ortalama fiyatını (örneğin merkezi eğilim ölçüsü) bilselerdi, o zaman aramalarını çok daha hızlı bir şekilde hassaslaştırabilirlerdi çünkü hangi mahallenin bütçelerine uygun ev fiyatlarına sahip olduğunu daha kolay tespit edebilirlerdi:
A mahallesindeki bir evin ortalama fiyatı: 220.000 $
B mahallesindeki bir evin ortalama fiyatı: 190.000 $
C mahallesindeki bir evin ortalama fiyatı: 140.000 $
Her mahalledeki ortalama ev fiyatını bilerek, Mahalle C’nin bütçeleri dahilinde en fazla mevcut evin bulunabileceğini hemen görebilirler.
Bu, merkezi eğilim ölçüsü kullanmanın yararıdır: veri değerlerinin genellikle nerede bulunduğunu açıklama eğiliminde olan bir veri kümesinin merkezi değerini anlamanıza yardımcı olur. Bu özel örnekte, genç çiftin her mahalledeki bir evin tipik fiyatını anlamasına yardımcı oluyor.
Çıkarım: Merkezi eğilim ölçüsü faydalıdır çünkü bize bir veri kümesinin “merkezini” tanımlayan tek bir değer sağlar. Bu, bir veri kümesini yalnızca veri kümesindeki tüm bireysel değerlere bakmaktan çok daha hızlı anlamamıza yardımcı olur.
Anlam
Merkezi eğilim ölçümünde en sık kullanılan ölçü ortalamadır . Bir veri kümesinin ortalamasını hesaplamak için tüm bireysel değerleri toplayıp toplam değer sayısına bölmeniz yeterlidir.
Ortalama = (tüm değerlerin toplamı) / (toplam değer sayısı)
Örneğin, bir sezon boyunca aynı takımdaki 10 beyzbol oyuncusunun isabetli sayılarını gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Oyuncu başına isabet eden ortalama home run sayısı şu şekilde hesaplanabilir:
Ortalama = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 devre .
Medyan
Medyan, bir veri kümesinin ortadaki değeridir. Bir veri kümesindeki tüm bireysel değerleri küçükten büyüğe sıralayıp ortanca değerini bularak ortancayı bulabilirsiniz. Tek sayıda değer varsa ortanca değer ortadaki değerdir. Çift sayıda değer varsa medyan ortadaki iki değerin ortalamasıdır.
Örneğin, önceki örnekte 10 beyzbol oyuncusunun vurduğu home runların medyan sayısını bulmak için, oyuncuları vurulan home run sayısına göre azalan sırada sıralayabiliriz:
| oyuncu | #1 | #6 | #7 | #5 | #on | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Çift sayıda değere sahip olduğumuz için medyan, ortadaki iki değerin ortalamasıdır: 13,5 .
Bunun yerine dokuz oyuncumuz olup olmadığını düşünün:
| oyuncu | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Bu durumda, tek sayıda değere sahip olduğumuz için medyan sadece ortadaki değerdir: 14 .
Moda
Mod, bir veri setinde en sık görülen değerdir. Bir veri kümesinde hiçbir mod (eğer hiçbir değer tekrarlanmıyorsa), bir mod veya birden fazla mod bulunabilir.
Örneğin, aşağıdaki veri kümesinin modu yoktur:
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Aşağıdaki veri kümesinin bir modu vardır: 15 . Bu en sık görülen değerdir.
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Aşağıdaki veri kümesinin üç modu vardır: 8, 15, 19 . Bunlar en sık görülen değerlerdir.
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Mod, kategorik verilerle çalışırken özellikle yararlı bir merkezi eğilim ölçüsü olabilir çünkü bize hangi kategorinin en sık göründüğünü söyler. Örneğin, insanların en sevdiği renkle ilgili bir anketin sonuçlarını gösteren aşağıdaki çubuk grafiği düşünün:
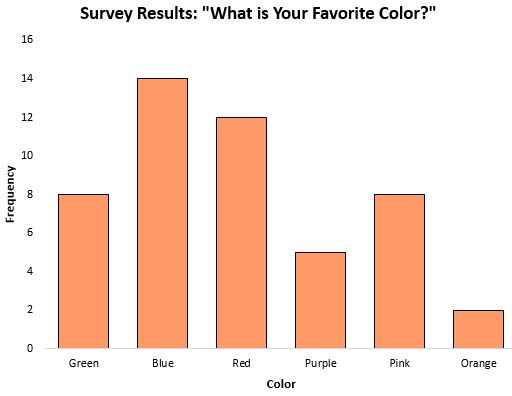
Mod veya en sık meydana gelen yanıt maviydi.
Verilerin kategorik olduğu senaryolarda (yukarıdaki gibi), medyanı veya ortalamayı hesaplamak bile mümkün değildir, dolayısıyla mod, kullanabileceğimiz tek merkezi eğilim ölçüsüdür.
Bu mod aynı zamanda yukarıdaki örnekte beyzbol oyuncuları ile gördüğümüz gibi sayısal veriler için de kullanılabilir. Ancak mod , “Bu veri kümesi için tipik değer nedir?” sorusunun yanıtlanmasında daha az yararlı olma eğilimindedir. »
Örneğin, bu takımdaki bir beyzbol oyuncusunun vurduğu sayının tipik sayısını bilmek istediğimizi varsayalım:
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Bu veri kümesinin modu 8, 15 ve 19’dur çünkü bunlar en sık görülen değerlerdir. Ancak bunlar, takımdaki bir oyuncunun vurduğu tipik home run sayısını anlamada pek yardımcı olmuyor. Bu durumda merkezi eğilimin daha iyi bir ölçüsü medyan (15) veya ortalama (yine 15) olacaktır.
Mod aynı zamanda diğer değerlerden uzak bir sayı olduğunda merkezi eğilimin zayıf bir ölçüsüdür. Örneğin, aşağıdaki veri setinin modu 30’dur, ancak bu aslında takımdaki oyuncu başına düşen “tipik” home run sayısını temsil etmez:
| oyuncu | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #on |
|---|---|---|---|---|---|---|---|---|---|---|
| Ev koşuları | 5 | 6 | 7 | on | 11 | 12 | 13 | 15 | 30 | 30 |
Yine ortalama veya medyan, bu veri setinin merkezi konumunu tanımlamada daha iyi bir iş çıkaracaktır.
Ortalama, Medyan ve Mod Ne Zaman Kullanılmalı?
Ortalamanın, medyanın ve modun hepsinin bir veri kümesinin merkezi konumunu veya “tipik değerini” çok farklı şekillerde ölçtüğünü gördük:
Ortalama: Bir veri kümesindeki ortalama değeri bulur.
Medyan: Bir veri kümesindeki medyan değerini bulur.
Mod: Bir veri kümesinde en sık görülen değeri bulur.
Bazı merkezi eğilim ölçülerinin kullanımının diğerlerinden daha iyi olduğu senaryolar şunlardır:
Ortalama ne zaman kullanılır?
Veri dağılımı oldukça simetrik olduğunda ve aykırı değerler olmadığında ortalamayı kullanmak en iyisidir.
Örneğin, belirli bir şehirdeki bireylerin maaşlarını gösteren aşağıdaki dağılıma sahip olduğumuzu varsayalım:

Bu dağılım oldukça simetrik olduğundan (yani ikiye bölerseniz her iki yarı da kabaca eşit görünür) ve aykırı değerler olmadığından (örneğin aşırı yüksek maaşlar yok), ortalama bu veri setini tanımlamada iyi bir iş çıkaracaktır.
Ortalama 63.000 dolar olarak ortaya çıkıyor ve bu da kabaca dağılımın merkezinde yer alıyor:

Medyan ne zaman kullanılır?
Veri dağılımı çarpık olduğunda veya aykırı değerler olduğunda medyanı kullanmak en iyisidir.
Önyargılı veriler:
Dağıtım çarpık olduğunda medyan yine de merkezi konumu yakalamayı başarır. Örneğin belirli bir şehirdeki bireylerin maaşlarının aşağıdaki dağılımını düşünün:

Medyan, bireyin “tipik” maaşını ortalamadan daha iyi yansıtır. Bunun nedeni, bir dağılımın kuyruğundaki büyük değerlerin ortalamayı merkezden uzun kuyruğa doğru kaydırma eğiliminde olmasıdır.
Bu özel örnekte, ortalama bize bu şehirde tipik bir bireyin yılda yaklaşık 47.000 dolar kazandığını söylerken medyan bize tipik bir bireyin yılda yalnızca 32.000 dolar civarında kazandığını söylüyor, bu da tipik bir bireyi çok daha iyi temsil ediyor.
Aykırı Değerler:
Medyan ayrıca verilerde aykırı değerler olduğunda dağılımın merkezi konumunun daha iyi yakalanmasına yardımcı olur. Örneğin, belirli bir caddedeki evlerin metrekaresini gösteren aşağıdaki grafiği düşünün:

Ortalama, birkaç aşırı büyük evden büyük ölçüde etkilenirken, medyan etkilenmemektedir. Böylece medyan, o sokaktaki bir evin “tipik” metrekaresini yakalama konusunda ortalamadan daha iyi bir iş çıkarıyor.
Modu ne zaman kullanmalı?
Bu mod, kategorik verilerle çalışırken ve hangi kategorinin en sık göründüğünü bilmek istediğinizde en iyi şekilde kullanılır. İşte bazı örnekler:
- İnsanların en sevdiği renkler üzerine bir anket yapıyorsunuz ve yanıtlarda en sık hangi rengin göründüğünü bilmek istiyorsunuz.
- İnsanların web sitesi tasarımı için üç seçenek arasından tercihlerini ölçen bir anket yapıyorsunuz ve insanların en çok hangi tasarımı tercih ettiğini bilmek istiyorsunuz.
Daha önce de belirtildiği gibi, kategorik verilerle çalışıyorsanız medyanı veya ortalamayı hesaplamak bile mümkün değildir, bu da modu merkezi eğilimin tek ölçüsü olarak bırakır.
Genel olarak, evlerin metrekaresi, oyuncu başına isabet eden sayı sayısı, kişi başına maaş vb. gibi sayısal verilerle çalışıyorsanız, “tipik” değeri tanımlamak için genellikle medyan veya ortalamayı kullanmak en iyisidir. veri kümesi.
Not: Bir veri kümesi tamamen normal bir şekilde dağılıyorsa ortalama, medyan ve modun hepsinin aynı değere sahip olacağını unutmamak önemlidir.