Merkezi limit teoremi

İle Dr.benjamin anderson Ağustos 1, 2023 Olasılık 0 Yorum

Bu makale merkezi limit teoreminin (CLT) ne olduğunu ve istatistikte ne için kullanıldığını açıklamaktadır. Ayrıca merkezi limit teoreminin formülünün ne olduğunu ve bunun adım adım çözülmüş bir uygulama örneğini bulacaksınız.

Merkezi limit teoremi nedir?

İstatistikte, merkezi limit teoremi olarak da adlandırılan merkezi limit teoremi , popülasyonun olasılık dağılımına bakılmaksızın , numune ortalamalarının dağılımının , numune boyutu arttıkça normal bir dağılıma yaklaştığını belirtir.

Yani, merkezi limit teoremi, yeterince fazla sayıda örnek alırsak, bu örneklerin ortalamasının normal dağılıma yaklaşabileceğini söylüyor.

Ek olarak merkezi limit teoremi, örneklem büyüklüğü arttıkça örneklem ortalamasının popülasyon ortalamasının değerine yaklaşacağını belirtir. Bu, istatistiksel popülasyonun parametrelerini yaklaşık olarak tahmin etmemizi sağlar. Aşağıda bunun nasıl yapıldığını göreceğiz.

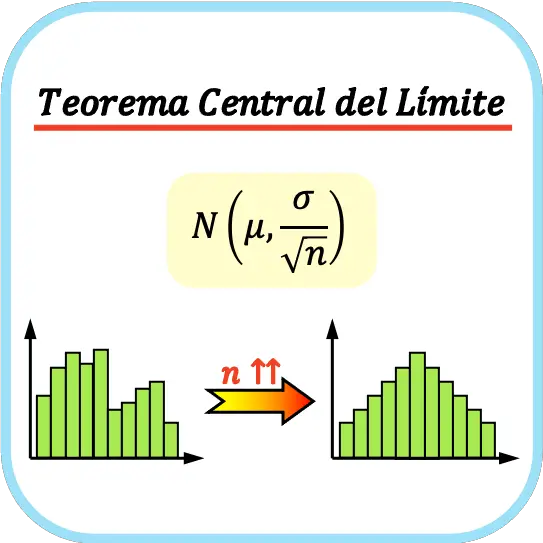
merkezi limit teoremi, merkezi limit teoremi

Genel olarak merkezi limit teoreminin uygulanabilmesi için örneklem büyüklüğünün en az 30 gözlem olması gerektiği düşünülmektedir, ancak bu durum çalışılan değişkenin özelliklerine bağlıdır.

Merkezi limit teoreminin birçok uygulaması vardır, çünkü normal dağılım hipotez testi veya güven aralıkları gibi çıkarımsal istatistiksel hesaplamalara izin verir. Örneğin finansta, bir yatırımın getirisini ve riskini analiz etmek için merkezi limit teoremi kullanılır.

➤ Bakınız: Normal dağılım nedir?

Merkezi limit teoremine örnek

Merkezi limit teoreminin tanımını gördükten sonra anlamını tam olarak anlamak için bir örneğe bakalım.

Merkezi limit teoreminin bir örneği, bir zarın yuvarlanmasıdır. Tüm sonuçlar eşit olasılıklı olduğundan, kalıp rulosu ayrık bir düzgün dağılım izler. Ancak birkaç sonucun toplamının dağılımı normal dağılıma yaklaşmaktadır.

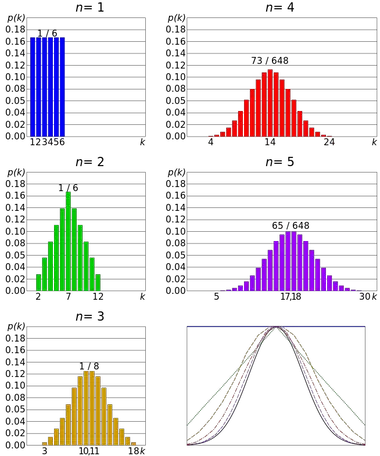
Dolayısıyla, ne kadar çok atış varsa, ortalamaların dağılım şeklinin normal dağılım grafiğine benzeme olasılığı da o kadar artar.

Merkezi Limit Teoremi Formülü

Merkezi limit teoremi, eğer bir popülasyon ortalama μ ve standart sapma σ’ya sahipse ve yeterince fazla sayıda örnek alırsak (n≥30), örnek ortalamaları kümesinin ortalama μ ve standart sapma σ ile normal bir dağılıma yaklaştırılabileceğini belirtir. /√n.

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

Ayrıca X ₁ _ise aşağıdaki formülle tanımlanan normal dağılıma _göre :

$\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

Merkezi limit teoreminin çözülmüş alıştırması

Kavramı tamamen özümseyebilmeniz için burada merkezi limit teoreminin çözülmüş bir alıştırmasını bulacaksınız.

Bir şirket, belirli oyuncak bileşenlerinin yerine kullanılan parçaları satıyor. Bir madeni paranın ortalama ağırlığı 300 gram, standart sapması ise 50 gramdır. Bir müşteri 100 parçalık bir parti sipariş ederse, partideki parçaların ortalama ağırlığının 305 gramdan fazla olma olasılığı nedir? Peki 100 parçadan oluşan bir partinin ağırlığının 31 kg’dan fazla olma olasılığı nedir?

Parti boyutu büyük olduğundan (n=100), sorunu çözmek için merkezi limit teoremini uygulayabiliriz.

Böylece, merkezi limit teoremi formülünü kullanarak, örnek ortalamaların dağılımı aşağıdaki parametrelerle normal dağılıma yaklaştırılabilir:

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

$\mu_{\overline{X}}=\mu=300$

$\sigma_{\overline{X}}=\cfrac{\sigma}{\sqrt{n}}=\cfrac{50}{\sqrt{100}}=5$

$\displaystyle N\left(300,5\right)$

Şimdi alıştırmanın bizden istediği olasılığı bulabilmek için yazma işlemini gerçekleştiriyoruz. Bunu yapmak için ortalamayı dağılımdan çıkarmamız ve ardından standart sapmaya bölmemiz gerekir:

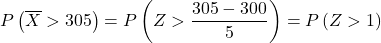$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>\frac{305-300}{5}\right)=P\left(Z>1\right)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”381″ style=”vertical-align: -17px;”> Dolayısıyla partideki parçaların ortalama ağırlığının 305 g’dan büyük olma olasılığını bulmak için <a href=$ normal dağılım tablosunda Z>1 değerinin hangi değere karşılık geldiğine bakmamız gerekir:

$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>1\right)=0,1587″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”276″ style=”vertical-align: -7px;”> Öte yandan, merkezi limit teoremi sayesinde 100 adetlik bir partinin normal dağılıma yaklaşabileceğini biliyoruz çünkü tüm madeni paralar aynı dağılımı takip ediyor. Bu nedenle, 100 madeni paradan oluşan bir partinin 31 kg’dan daha ağır olma olasılığını belirlemek için merkezi limit teoreminin diğer formülünü uygulamamız gerekir: <p class=$ $\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

$\displaystyle Y\sim N\left(100\cdot 300,50\cdot \sqrt{100}\right)$

$\displaystyle Y\sim N\left(30000,500\right)$

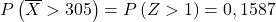
Böylece yazma işlemini yeniden yapıyoruz ve ardından sorunun bize sorduğu ikinci olasılığı buluyoruz:

$\displaystyle P\left(Y>31000\right)=P\left(Z>\frac{31000-30000}{500}\right)=P\left(Z>2\right)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”430″ style=”vertical-align: -17px;”> Son olarak, normal dağılım tablosunu kullanarak 100 parçalık bir partinin 31 kg’dan fazla ağırlığa sahip olma olasılığını belirleyebiliriz: 31000\right)=P\left(Z>2\right)=0,0228″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”289″ style=”vertical-align: -5px;”> <div style=$ ➤ 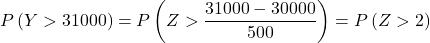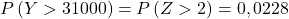Bakınız: Büyük sayılar kanunu

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil