Excel'de merkezi limit teoremi nasıl uygulanır?

Merkezi limit teoremi, popülasyon dağılımı normal olmasa bile, örneklem büyüklüğü yeterince büyükse, bir örneklem ortalamasının örnekleme dağılımının yaklaşık olarak normal olduğunu belirtir.

Merkezi limit teoremi ayrıca örnekleme dağılımının aşağıdaki özelliklere sahip olacağını belirtir:

1. Örnekleme dağılımının ortalaması nüfus dağılımının ortalamasına eşit olacaktır:

x = µ

2. Örnekleme dağılımının standart sapması, popülasyon standart sapmasının örneklem büyüklüğüne bölünmesine eşit olacaktır:

s = σ / √n

Bu derste Excel’deki merkezi limit teoreminin belirli bir dağılıma nasıl uygulanacağını açıklıyoruz.

Excel’de Merkezi Limit Teoremini Uygulamak

Ortalaması 8 ve standart sapması 4 olan bir dağılıma sahip olduğumuzu varsayalım. Örneklem büyüklüğü 15 olan örnekleme dağılımının hem ortalamasını hem de standart sapmasını bulmak için Excel’de aşağıdaki formülleri kullanabiliriz:

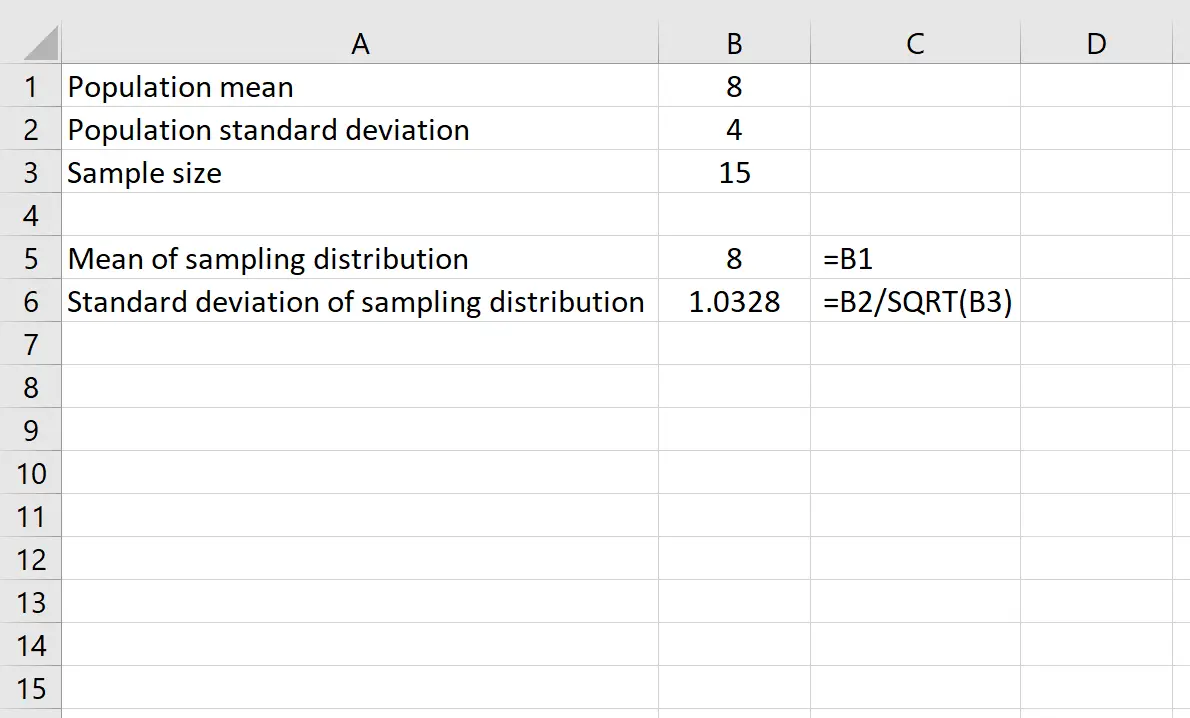
Örnekleme dağılımının ortalaması, nüfus dağılımının ortalamasına yani 8’e eşittir.

Örnekleme dağılımının standart sapması, popülasyon standart sapmasının örneklem büyüklüğüne bölünmesine eşittir veya: 4 /√15 = 1,0328 .

Olasılıkla ilgili soruları yanıtlamak için merkezi limit teoremini de kullanabiliriz. Örneğin, belirli bir popülasyonun ortalaması 8 ve standart sapması 4 ise, belirli bir örneklem büyüklüğünün 15 olması olasılığı nedir?   ortalaması 7’den küçük veya ona eşit mi?

Bu soruyu yanıtlamak için Excel’de aşağıdaki sözdizimini kullanan NORM.DAĞ() işlevini kullanabiliriz:

NORM.DAĞ(x, ortalama, standart_sapma, kümülatif)

Altın:

• x: örnek, test etmek istediğiniz anlamına gelir
• ortalama: örnekleme dağılımının beklenen ortalaması
• standard_dev: örnekleme dağılımının beklenen standart sapması
• kümülatif: DOĞRU normal CDF değerini döndürür; FALSE, normal PDF’nin değerini döndürür. Bizim durumumuzda her zaman TRUE’yu kullanacağız.

Bu fonksiyon, örnek ortalamasının belirli bir değerden küçük veya ona eşit olma olasılığını döndürecektir.

Bu örnekte kullanacağımız formül şu şekildedir:

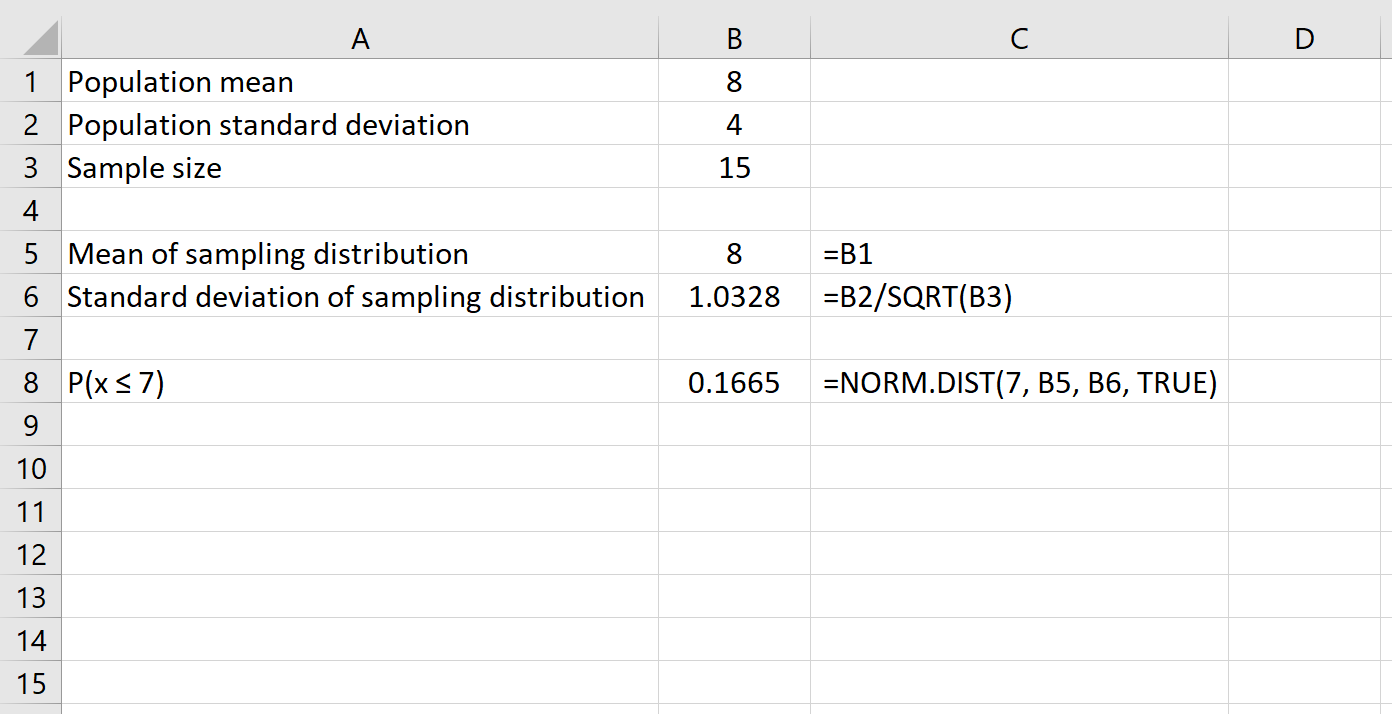
Bu bize ortalaması 8 ve standart sapması 4 olan bir popülasyon için belirli büyüklükteki bir örneğin 15 olma olasılığının olduğunu söyler.   ortalaması 7 veya 0,1665’ten küçük veya ona eşittir.

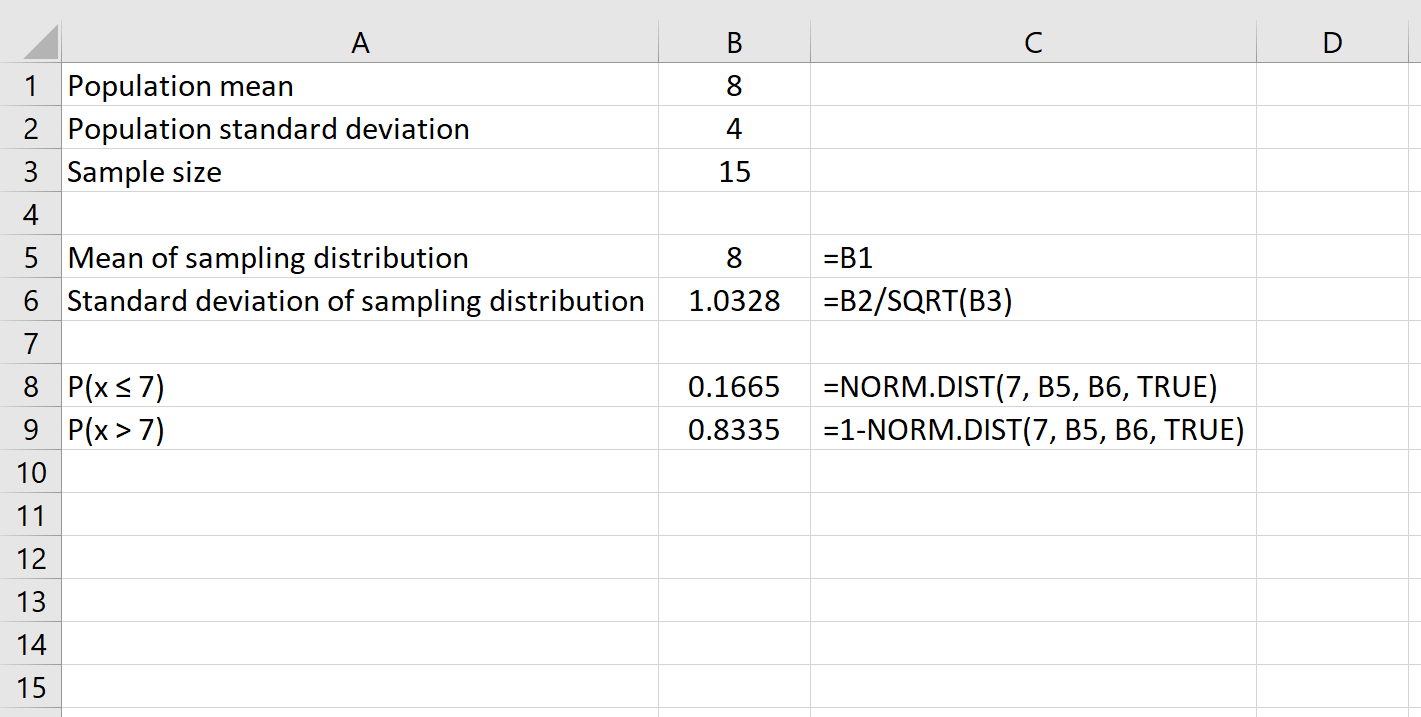
Belirli bir örnek boyutunun belirli bir sayıdan daha büyük bir ortalamaya sahip olma olasılığını da basitçe formül 1 – NORM.DAĞ() kullanarak bulabiliriz.

Örneğin, aşağıdaki formül, 15 kişilik belirli bir örneklem büyüklüğünün 7’den büyük bir ortalamaya sahip olma olasılığının nasıl belirleneceğini gösterir:

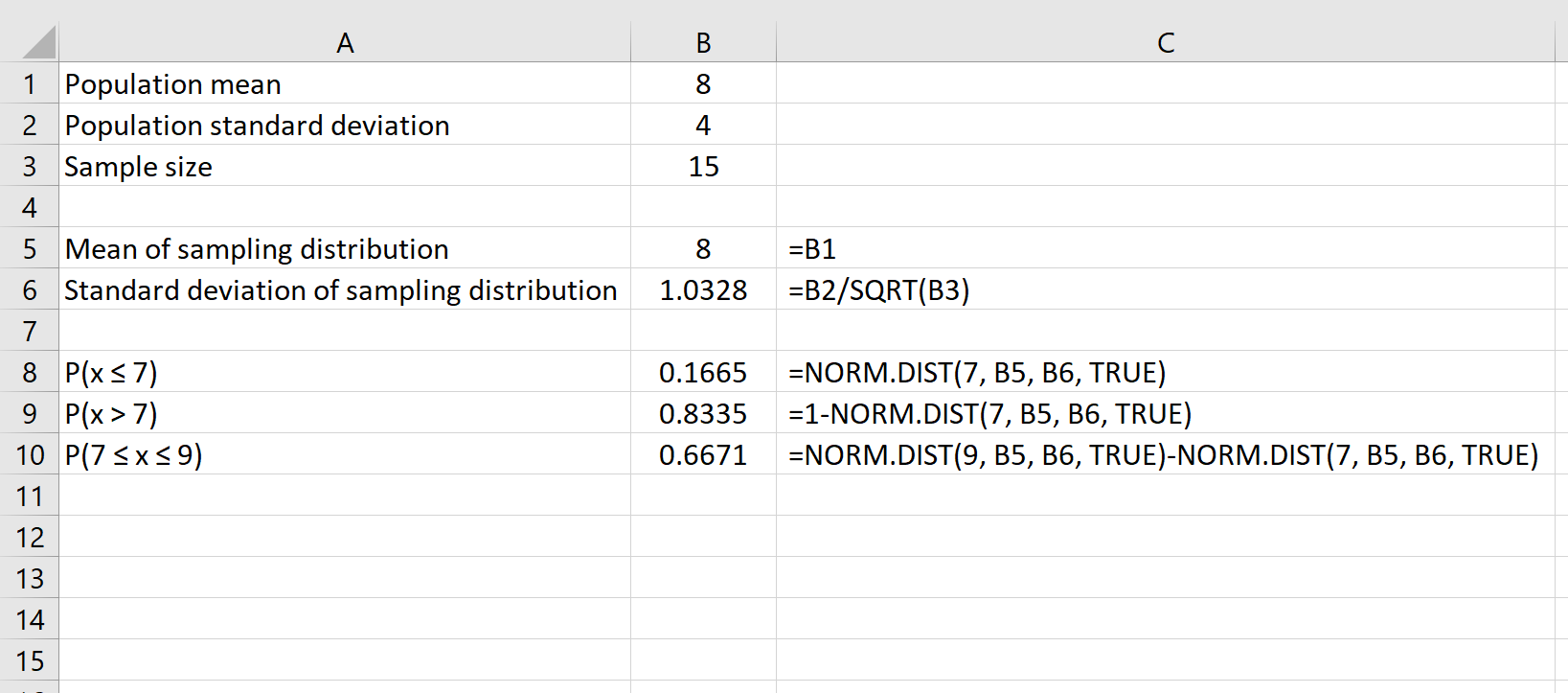
Son olarak, NORM.DAĞ(daha büyük sayı) – NORM.DAĞ(daha küçük sayı) formülünü kullanarak belirli bir örneklem büyüklüğünün iki sayı arasında bir ortalamaya sahip olma olasılığını bulabiliriz.

Örneğin, aşağıdaki formül, belirli bir örneklem büyüklüğü olan 15’in ortalamasının 7 ile 9 arasında olması olasılığının nasıl bulunacağını gösterir:

Ek kaynaklar

Merkezi Limit Teoremi Hesaplayıcı
Excel’de temel kural nasıl uygulanır?
Excel’de Çan Eğrisi Nasıl Oluşturulur