Ti-84 hesap makinesinde merkezi limit teoremi nasıl uygulanır?

Merkezi limit teoremi, popülasyon dağılımı normal olmasa bile, örneklem büyüklüğü yeterince büyükse, bir örneklem ortalamasının örnekleme dağılımının yaklaşık olarak normal olduğunu belirtir.

Merkezi limit teoremi ayrıca örnekleme dağılımının aşağıdaki özelliklere sahip olacağını belirtir:

1. Örnekleme dağılımının ortalaması nüfus dağılımının ortalamasına eşit olacaktır:

x = µ

2. Örnekleme dağılımının standart sapması, popülasyon standart sapmasının örneklem büyüklüğüne bölünmesine eşit olacaktır:

s = σ / √n

Bir TI-84 hesap makinesinde örnek ortalamayla ilgili olasılıkları bulmak için normalcdf() işlevini aşağıdaki sözdizimiyle kullanabiliriz:

 normalcdf (lower value, upper value, x , s/√ n )

Altın:

• x : örnek ortalama
• s : numune standart sapması
• n : örneklem büyüklüğü

Bu fonksiyona TI-84 hesap makinesinde erişmek için 2nd tuşuna, ardından VARS tuşuna basıp normalcdf’ye ( ve ENTER tuşuna basmanız yeterlidir.

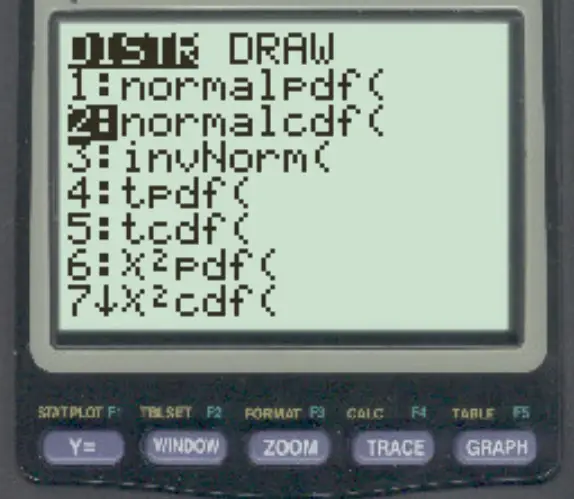
Aşağıdaki örnekler bu fonksiyonun pratikte nasıl kullanılacağını göstermektedir.

Örnek 1: İki değer arasındaki olasılığı bulun

Bir dağılımın ortalaması 70 ve standart sapması 7’dir. Eğer n = 35 büyüklüğünde rastgele bir örneklem seçersek, örneklem ortalamasının 68 ile 72 arasında olma olasılığını bulun.

TI-84’te aşağıdaki sözdizimini kullanabiliriz:

 normalcdf (68, 72, 70, 7/√ 35 ) 

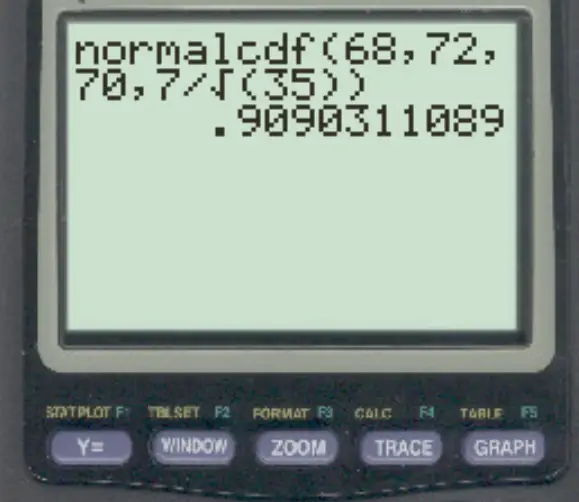
Örneklem ortalamasının 68 ile 72 arasında olma olasılığı 0,909’dur .

Örnek 2: Bir değerden daha büyük bir olasılığı bulma

Bir dağılımın ortalaması 50 ve standart sapması 4’tür. Eğer n = 30 boyutunda rastgele bir örneklem seçersek, örneklem ortalamasının 48’den büyük olma olasılığını bulun.

TI-84’te aşağıdaki sözdizimini kullanabiliriz:

 normalcdf (48, E99, 50, 4/√ 30 )

Not: “E” sembolüne 2 tuşuna ve ardından , tuşuna basarak ulaşabilirsiniz.

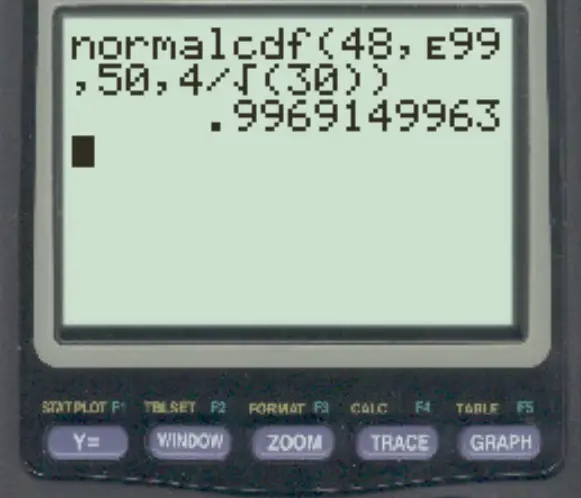
Örneklem ortalamasının 48’den büyük olma olasılığı 0,9969’dur .

Örnek 3: Bir değerden daha düşük bir olasılığı bulma

Bir dağılımın ortalaması 20 ve standart sapması 3’tür. Eğer n = 40 boyutunda rastgele bir örneklem seçersek, örneklem ortalamasının 19’dan küçük olma olasılığını bulun.

TI-84’te aşağıdaki sözdizimini kullanabiliriz:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

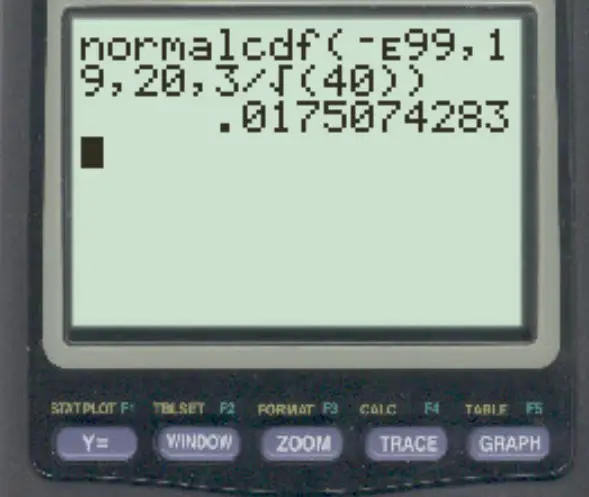
Örneklem ortalamasının 19’dan küçük olma olasılığı 0,0175’tir .

Ek kaynaklar

Merkezi Limit Teoremine Giriş
Merkezi Limit Teoremi Hesaplayıcı
Excel’de Merkezi Limit Teoremi Nasıl Uygulanır?
Merkezi limit teoremi: yerine getirilmesi gereken dört koşul