R'deki mtcars veri kümesine yönelik eksiksiz bir rehber

Mtcars veri seti, 32 farklı araba için 11 farklı özellik üzerinde ölçümler içeren R’deki entegre bir veri setidir.

Bu eğitimde, R’de mtcars veri kümesinin nasıl keşfedileceği, özetleneceği ve görselleştirileceği açıklanmaktadır.

İlgili: R’deki İris Veri Kümesine İlişkin Tam Bir Kılavuz

Mtcars veri kümesini yükle

Mtcars veri kümesi R’de yerleşik bir veri kümesi olduğundan, aşağıdaki komutu kullanarak yükleyebiliriz:

 data(mtcars)

Head() fonksiyonunu kullanarak veri setinin ilk altı satırına göz atabiliriz:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Mtcars veri kümesini özetleme

Veri kümesindeki her değişkeni hızlı bir şekilde özetlemek için Summary() işlevini kullanabiliriz:

 #summarize mtcars dataset
summary(mtcars)

      mpg cyl disp hp       
 Min. :10.40 Min. :4,000 Min. : 71.1 Min. : 52.0  
 1st Q:15.43 1st Q:4,000 1st Q:120.8 1st Q:96.5  
 Median: 19.20 Median: 6.000 Median: 196.3 Median: 123.0  
 Mean:20.09 Mean:6.188 Mean:230.7 Mean:146.7  
 3rd Q:22.80 3rd Q:8,000 3rd Q:326.0 3rd Q:180.0  
 Max. :33.90 Max. :8,000 Max. :472.0 Max. :335.0  
      drat wt qsec vs        
 Min. :2.760 Min. :1.513 Min. :14.50 Min. :0.0000  
 1st Qu.:3.080 1st Qu.:2.581 1st Qu.:16.89 1st Qu.:0.0000  
 Median: 3.695 Median: 3.325 Median: 17.71 Median: 0.0000  
 Mean:3.597 Mean:3.217 Mean:17.85 Mean:0.4375  
 3rd Qu.:3.920 3rd Qu.:3.610 3rd Qu.:18.90 3rd Qu.:1.0000  
 Max. :4.930 Max. :5.424 Max. :22.90 Max. :1.0000  
       am gear carb      
 Min. :0.0000 Min. :3,000 Min. :1,000  
 1st Qu.:0.0000 1st Qu.:3.000 1st Qu.:2.000  
 Median: 0.0000 Median: 4.000 Median: 2.000  
 Mean:0.4062 Mean:3.688 Mean:2.812  
 3rd Qu.:1.0000 3rd Qu.:4.000 3rd Qu.:4.000  
 Max. :1.0000 Max. :5,000 Max. :8,000

11 değişkenin her biri için aşağıdaki bilgileri görebiliriz:

• Min : Minimum değer.
• 1st Qu : İlk çeyreğin değeri (25. yüzdelik dilim).
• Medyan : Medyan değeri.
• Ortalama : Ortalama değer.
• 3rd Qu : Üçüncü çeyreğin değeri (75. yüzdelik).
• Maks : Maksimum değer.

Veri kümesinin boyutlarını satır ve sütun sayısına göre elde etmek için dim() işlevini kullanabiliriz:

 #display rows and columns
dim(mtcars)

[1] 32 11

Veri setinin 32 satır ve 11 sütundan oluştuğunu görüyoruz.

Veri çerçevesinin sütun adlarını görüntülemek için labels() işlevini de kullanabiliriz:

 #display column names
names(mtcars)

 [1] "mpg" "cyl" "disp" "hp" "drat" "wt" "qsec" "vs" "am" "gear"
[11] “carb”     

Mtcars veri kümesini görselleştirin

Veri kümesinin değerlerini görselleştirmek için grafikler de oluşturabiliriz.

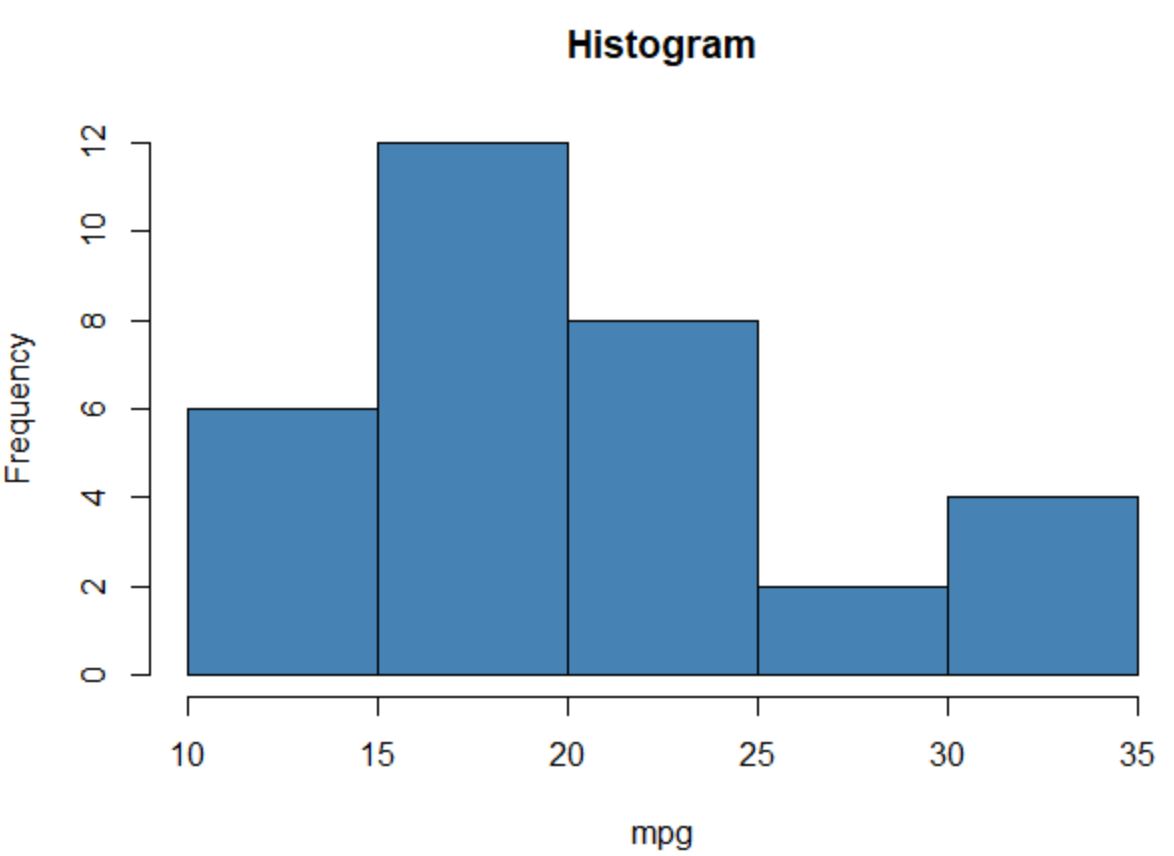
Örneğin, belirli bir değişkenin değerlerinin histogramını oluşturmak için hist() fonksiyonunu kullanabiliriz:

 #create histogram of values for mpg
hist(mtcars$mpg,
     col=' steelblue ',
     main=' Histogram ',
     xlab=' mpg ',
     ylab=' Frequency ')

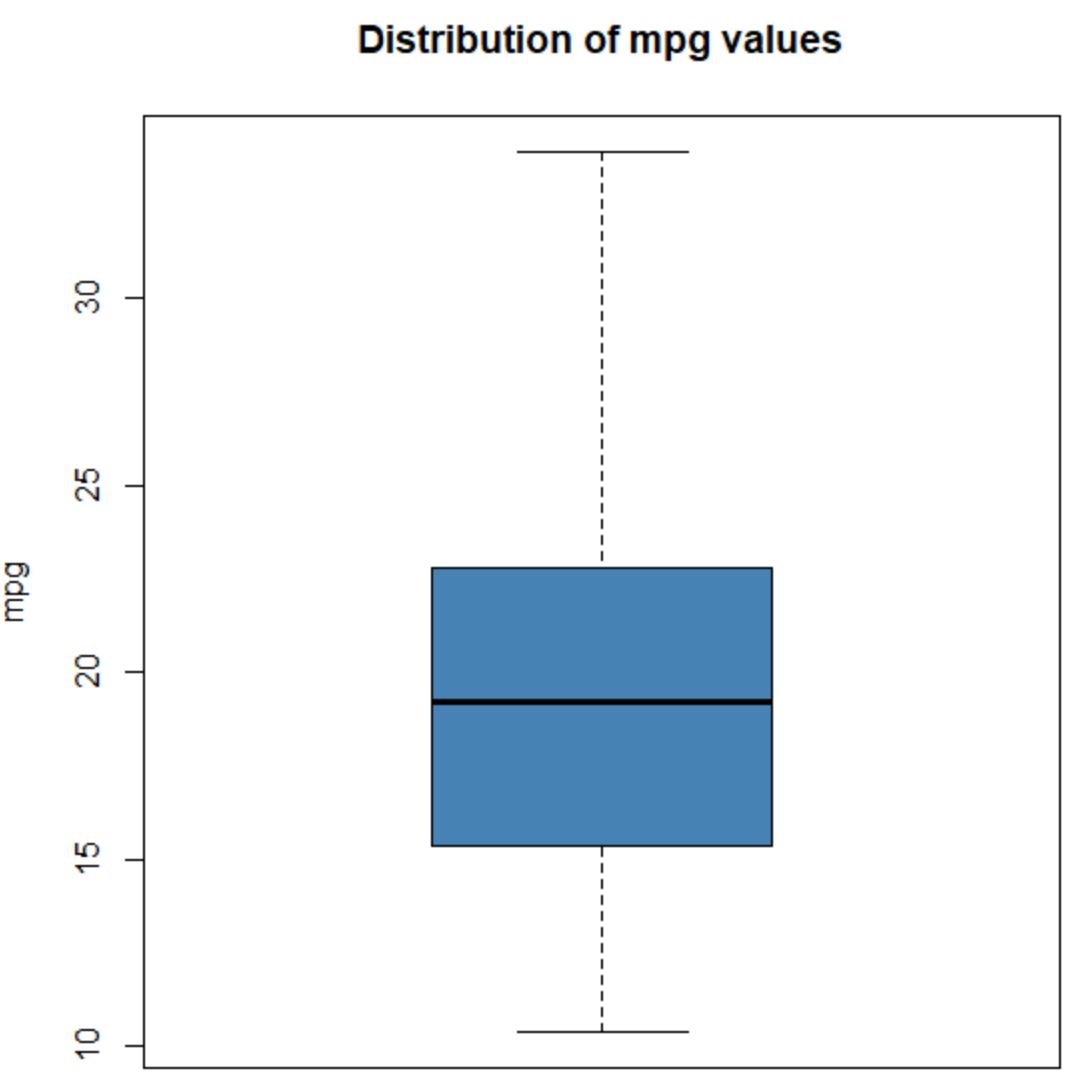
Belirli bir değişkene ilişkin değerlerin dağılımını görselleştirmek amacıyla bir kutu grafiği oluşturmak için boxplot() işlevini de kullanabiliriz:

 #create boxplot of values for mpg
boxplot(mtcars$mpg,
        main=' Distribution of mpg values ',
        ylab=' mpg ',
        col=' steelblue ',
        border=' black ') 

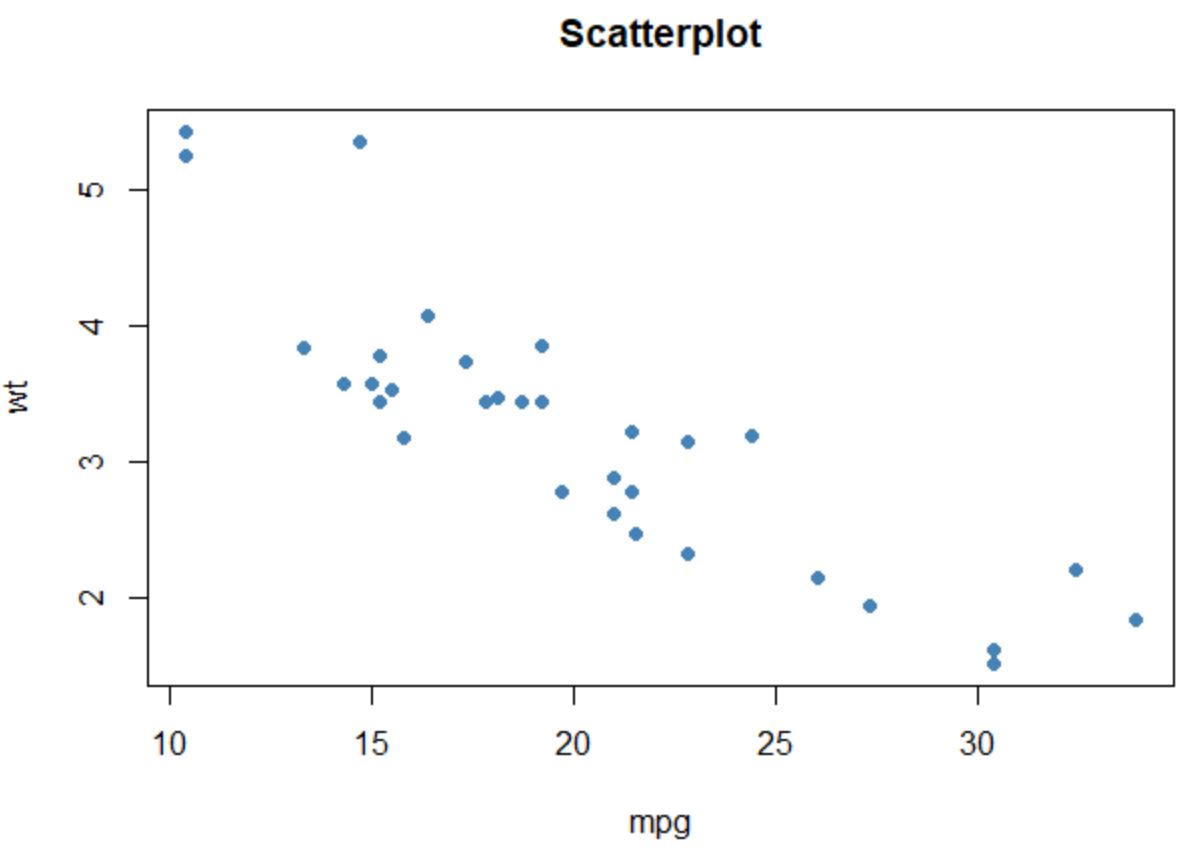
Değişkenlerin herhangi bir ikili kombinasyonunun dağılım grafiğini oluşturmak için de arsa() fonksiyonunu kullanabiliriz:

 #create scatterplot of mpg vs. wt
plot(mtcars$mpg, mtcars$wt,
     col=' steelblue ',
     main=' Scatterplot ',
     xlab=' mpg ',
     ylab=' wt ',
     pch= 19 ) 

R’deki bu yerleşik işlevleri kullanarak mtcars veri kümesi hakkında çok şey öğrenebiliriz.

Bu veri kümesiyle daha gelişmiş istatistiksel analiz gerçekleştirmek istiyorsanız mtcars veri kümesini kullanarak doğrusal regresyon modellerinin ve genelleştirilmiş doğrusal modellerin nasıl sığdırılacağını açıklayan bu eğitime göz atın.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de özet tablolar oluşturmanın en kolay yolu
R’deki beş sayının özeti nasıl hesaplanır
R’de basit doğrusal regresyon nasıl gerçekleştirilir