Birikmiş mutlak frekans

Bu makalede, birikmiş mutlak frekansın ne olduğu ve ne için kullanıldığı açıklanmaktadır. Böylece kümülatif mutlak frekansın tanımını, bir veri setinden kümülatif mutlak frekansın nasıl elde edileceğini ve ayrıca adım adım çözülen iki alıştırmayı bulacaksınız.

Kümülatif mutlak frekans nedir?

İstatistikte kümülatif mutlak frekans , mutlak frekansların kümülatif toplamıdır. Yani bir değerin kümülatif mutlak frekansı, o değerin mutlak frekansı artı ondan küçük tüm değerlerin mutlak frekanslarının toplamına eşittir.

Normalde istatistiklerde, i alt simgeli büyük F harfi, i değerinin kümülatif mutlak frekansını temsil etmek için kullanılır, dolayısıyla kümülatif mutlak frekansın sembolü F _i’dir .

Mantıksal olarak, birikmiş mutlak frekansın ne anlama geldiğini anlamak için mutlak frekans kavramı konusunda net olmanız gerekir, bu nedenle açıklamaya devam etmeden önce aşağıdaki makaleye göz atmanız önerilir.

Kümülatif mutlak frekans nasıl hesaplanır?

Kümülatif mutlak frekansı hesaplama adımları aşağıdaki gibidir:

1. Veri kümesinde görünen tüm farklı değerleri içeren bir tablo oluşturun, yani her farklı değeri bir tablonun satırına yerleştirin.
2. Her değerin mutlak frekansını belirler.
3. Her bir değerin kümülatif mutlak frekansını bulun; bu frekans, değerin kendisinin mutlak frekansı artı tüm küçük değerlerin mutlak frekanslarının eklenmesiyle hesaplanır.

Değişken sürekliyse veya çok sayıda farklı değer varsa, önce verileri aralıklara gruplandırmanız ve ardından kümülatif mutlak frekansı bulmak için yukarıda açıklanan adımları uygulamanız gerektiğini unutmayın.

Kümülatif Mutlak Frekans Örnekleri

Kümülatif mutlak frekansın nasıl hesaplandığını görebilmeniz için aşağıda gerçek dünyadan adım adım iki örnek verilmiştir. İlk örnekte ayrık bir değişkenin ve ikinci adımda sürekli bir değişkenin kümülatif mutlak frekansları hesaplandı.

Örnek 1: ayrık değişken

• 30 kişilik bir sınıfta istatistikten alınan notlar aşağıdaki gibidir. Her notanın kümülatif mutlak frekansı nedir?

Tüm sayılar yalnızca tam sayı olabildiği için ayrık bir değişkendir. Bu nedenle verileri aralıklar halinde gruplamak gerekli değildir.

Dolayısıyla, kümülatif mutlak frekansı belirlemek için öncelikle her değerin mutlak frekansını bulmamız gerekir; bu, her bir değerin istatistiksel örnekte görünme sayısıdır.

Artık mutlak frekansı bildiğimize göre kümülatif mutlak frekansı hesaplayabiliriz. Bunu yapmak için iki seçeneğimiz var: ya değerin mutlak frekansı artı en küçük değerlerin tüm mutlak frekanslarını topluyoruz ya da tam tersine, değerin mutlak frekansı artı önceki değerlerin kümülatif mutlak frekansını topluyoruz . değer.

Kısaca mutlak kümülatif egzersiz sıklığını gösteren tablo şu şekildedir:

Son değerin kümülatif mutlak frekansının her zaman toplam veri sayısına karşılık geldiğini unutmayın. Aksi halde hesaplamada hata yapmışsınız demektir.

Örnek 2: sürekli değişken

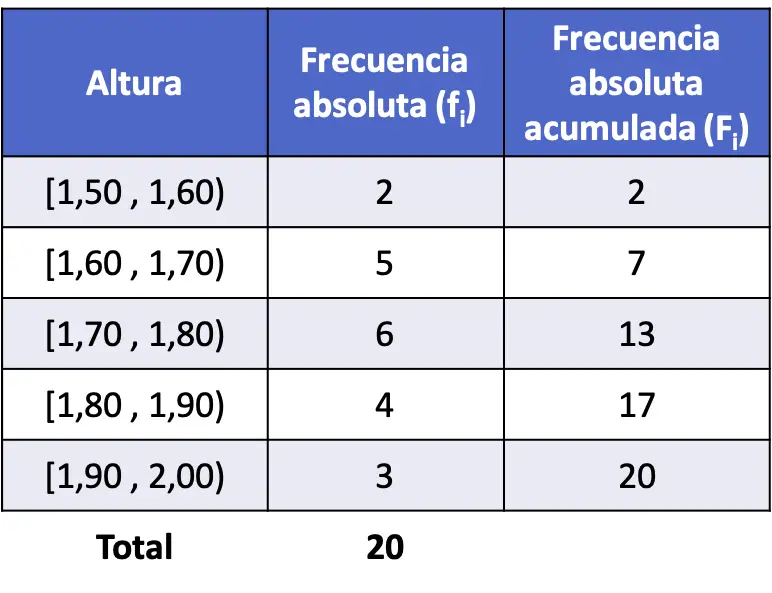
• 20 kişinin boyu ölçüldü ve aşağıdaki sonuçlar elde edildi. Verileri aralıklara ayırır ve her aralık için kümülatif mutlak frekansı hesaplar.

Bu örnekteki dağılım süreklidir çünkü ondalık sayılar olabilir, dolayısıyla verileri farklı aralıklara gruplamak en iyisidir.

Bu nedenle, verileri aralıklara ayırıyoruz ve mutlak frekansı elde etmek için her aralıkta bir sayının kaç kez göründüğünü sayıyoruz:

Daha sonra, kümülatif mutlak frekansı belirlemek için, önceki tüm değerlerin mutlak frekanslarını ve söz konusu değerin mutlak frekansını eklemeniz yeterlidir:

Kümülatif mutlak frekans ve kümülatif bağıl frekans

Kümülatif mutlak frekans ile kümülatif bağıl frekans arasındaki fark, kümülatif frekans tipine karşılık gelir. Birikmiş mutlak frekans, eşit veya daha düşük değerlerin mutlak frekanslarının toplamına eşitken, birikmiş bağıl frekans, eşit veya daha düşük değerlerin bağıl frekanslarına eşdeğerdir.

Yani kümülatif mutlak frekans mutlak frekanstan hesaplanırken, kümülatif bağıl frekans bağıl frekanstan hesaplanır.

Kümülatif bağıl frekans hesaplamasının bir örneğini burada görebilirsiniz: