Negatif binom dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede negatif binom dağılımının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Ayrıca negatif binom dağılımının formülünü, somut bir örneğini ve bu tür olasılık dağılımının özelliklerini de bulacaksınız. Son olarak, herhangi bir negatif binom dağılım olasılığını çevrimiçi bir hesap makinesiyle hesaplayabileceksiniz.

Negatif binom dağılımı nedir?

Negatif binom dağılımı, belirli sayıda pozitif sonuç elde etmek için gereken Bernoulli denemelerinin sayısını tanımlayan bir olasılık dağılımıdır.

Bu nedenle, negatif bir binom dağılımının iki karakteristik parametresi vardır: r , arzu edilen başarılı sonuçların sayısıdır ve p , gerçekleştirilen her Bernoulli deneyinin başarı olasılığıdır.

$X\sim \text{BN}(r,p)$

Bernoulli testinin iki olası sonucu olan bir deney olduğunu unutmayın: “başarı” ve “başarısızlık”. Yani “başarı” olasılığı p ise, “başarısızlık” olasılığı q=1-p’dir .

Dolayısıyla negatif binom dağılımı, pozitif sonuçlar elde etmek için gerektiği kadar Bernoulli denemesinin yapıldığı bir süreci tanımlar. Ayrıca, tüm bu Bernoulli denemeleri bağımsızdır ve sabit bir başarı olasılığına sahiptir.

Örneğin, negatif binom dağılımını takip eden rastgele bir değişken, 6 sayısı üç kez atılana kadar bir zarın kaç kez atılması gerektiğidir.

Negatif binom dağılımı ile binom dağılımı arasındaki fark, negatif binom dağılımının belirli sayıda başarılı sonuç elde etmek için gereken sayıyı sayması, binom dağılımının ise bir dizi Bernoulli testindeki başarılı vakaların sayısını saymasıdır.

➤ Bakınız: Binom dağılımı nedir?

Negatif binom dağılım formülü

r, p, x parametreleri göz önüne alındığında, negatif binom dağılımının olasılığı, xr’deki x-1’in kombinatoryal sayısının (1-p) ^xr ile p ^r ile çarpılmasıyla hesaplanır.

Dolayısıyla, negatif binom dağılım olasılığını hesaplamak için formül şöyledir:

👉Negatif binom dağılımını takip eden bir değişkenin olasılığını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Negatif binom dağılımının çözülmüş alıştırması

Bir parayı sekiz kez attığınızda, sekizinci atışta dördüncü kez tura gelme olasılığı nedir?

Öncelikle para atıldığında tura gelme olasılığını hesaplamamız gerekir. Bu durumda, iki olası sonuçtan (tura ve yazı) yalnızca bir pozitif sonuca (tura) sahibiz, dolayısıyla başarı olasılığı:

$p=\cfrac{1}{2}=0,5$

Dolayısıyla bu problemdeki rastgele değişken, r=4 ve p=0,5 olan negatif bir binom dağılımını takip eder. Bu nedenle, egzersizin bizden yapmamızı istediği olasılığı hesaplamak için negatif binom dağılım formülünü kullanıyoruz.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Negatif binom dağılımının özellikleri

Negatif binom dağılımının en önemli özellikleri aşağıda verilmiştir.

Negatif binom dağılımı iki karakteristik parametreyle tanımlanır: r , istenen başarılı sonuçların sayısıdır ve p , gerçekleştirilen her Bernoulli deneyinin başarı olasılığıdır.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

Negatif binom dağılımının varyansı, r çarpı (1-p) bölü p ^2’ye eşittir.

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

r parametresi 1’den büyükse, negatif binom dağılımının modu aşağıdaki formülle hesaplanabilir:

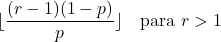
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> Negatif binom dağılımının olasılığını belirlemeyi mümkün kılan kütle fonksiyonu aşağıdaki gibidir:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Negatif binom dağılımının çarpıklık katsayısı aşağıdaki ifadeyle hesaplanır:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

Negatif binom dağılımının basıklığı aşağıdaki formülle bulunabilir:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Eğer r parametresi 1’e eşitse, geometrik dağılım durumuyla karşı karşıyayız.

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Negatif Binom Dağılımı Hesaplayıcı

Olasılığı hesaplamak için r, p, x parametrelerinin değerlerini aşağıdaki hesap makinesine girin. Sayıları ondalık ayırıcı olarak noktayı kullanarak girmelisiniz, örneğin 0,50.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil