Excel'de nokta tahminleri nasıl hesaplanır (örneklerle)
Nokta tahmini, bir popülasyon parametresini tahmin etmek için örnek verilerden hesapladığımız bir sayıyı temsil eder. Bu, gerçek popülasyon parametresinin ne olabileceğine dair mümkün olan en iyi tahminimizdir.
Aşağıdaki tablo popülasyon parametrelerini tahmin etmek için kullandığımız nokta tahminini göstermektedir:
| Ölçüm | Nüfus parametresi | Nokta tahmini |
|---|---|---|
| Anlam | μ (nüfus ortalaması) | x (örnek ortalama) |
| Oran | π (nüfus oranı) | p (örnek oranı) |
Bir nokta tahmini, bir popülasyon parametresine ilişkin en iyi tahminimizi temsil etse de, gerçek popülasyon parametresine tam olarak karşılık geleceği garanti edilmez.
Bu nedenle sıklıkla güven aralıklarını, yani belirli bir güven düzeyine sahip bir popülasyon parametresini içermesi muhtemel aralıkları da hesaplarız.
Aşağıdaki örnekler Excel’de nokta tahminlerinin ve güven aralıklarının nasıl hesaplanacağını göstermektedir.
Örnek 1: Bir popülasyon ortalamasının nokta tahmini
Bir kaplumbağa popülasyonunun ortalama ağırlığını hesaplamak istediğimizi varsayalım. Bunu yapmak için 20 kaplumbağadan rastgele bir örnek topluyoruz:
Nüfus ortalamasına ilişkin nokta tahminimiz basitçe örnek ortalamadır ve bunun 300,3 kitap olduğu ortaya çıkar:
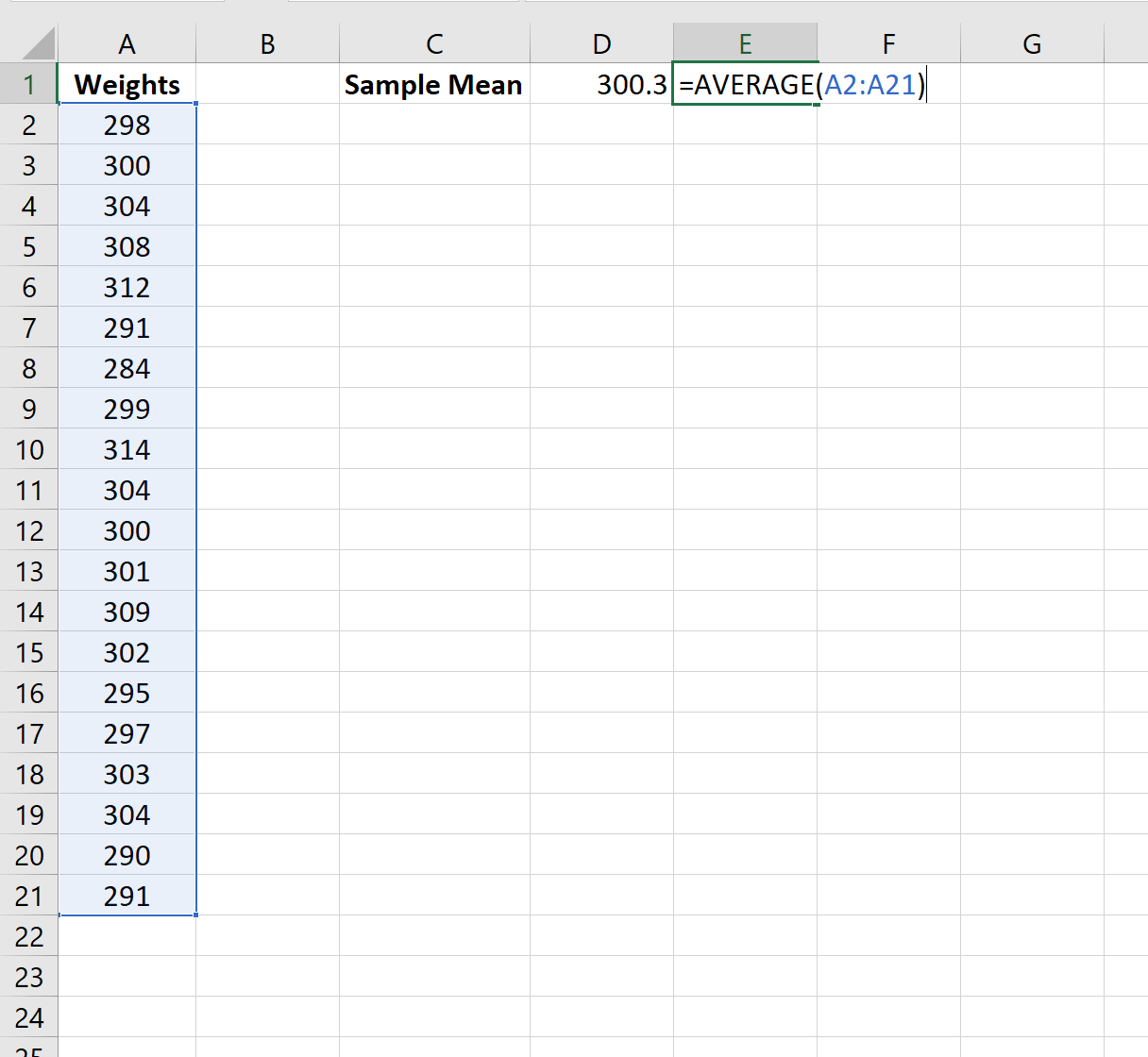
Daha sonra popülasyon ortalaması için %95 güven aralığını hesaplamak üzere aşağıdaki formülü kullanabiliriz:
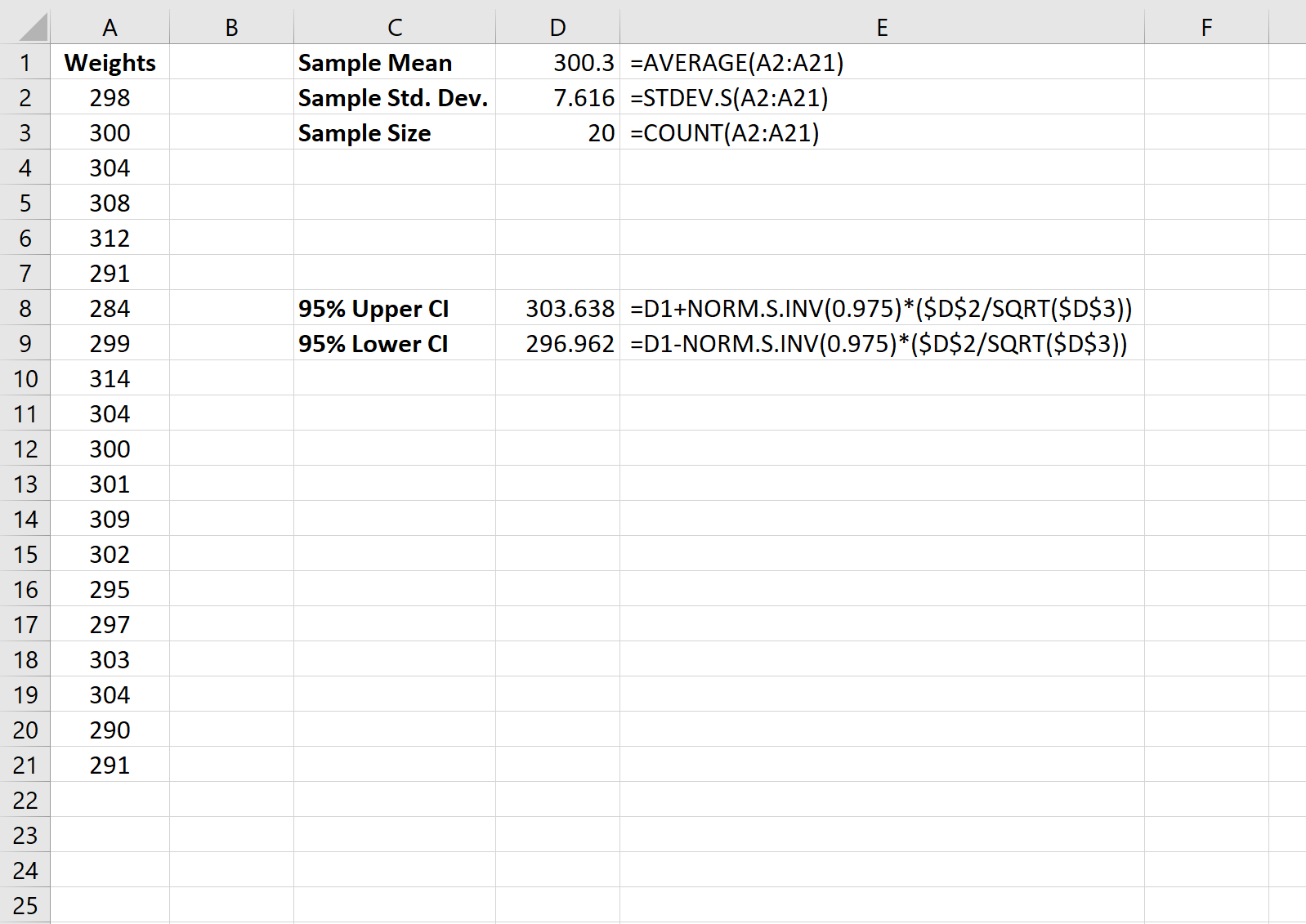
Bu popülasyondaki kaplumbağaların gerçek ortalama ağırlığının [296,96, 303,64] aralığında olduğundan %95 eminiz.
Bu sonuçları güven aralığı hesaplayıcısını kullanarak doğrulayabiliriz.
Örnek 2: Nüfus oranının nokta tahmini
Bir popülasyondaki kabuklarında lekeler bulunan kaplumbağaların oranını hesaplamak istediğimizi varsayalım. Bunu yapmak için 20 kaplumbağadan rastgele bir örnek topluyoruz ve bunlardan 13’ünün benekli olduğunu buluyoruz.
Benekli kaplumbağaların oranı için puan tahminimiz 0,65’tir :
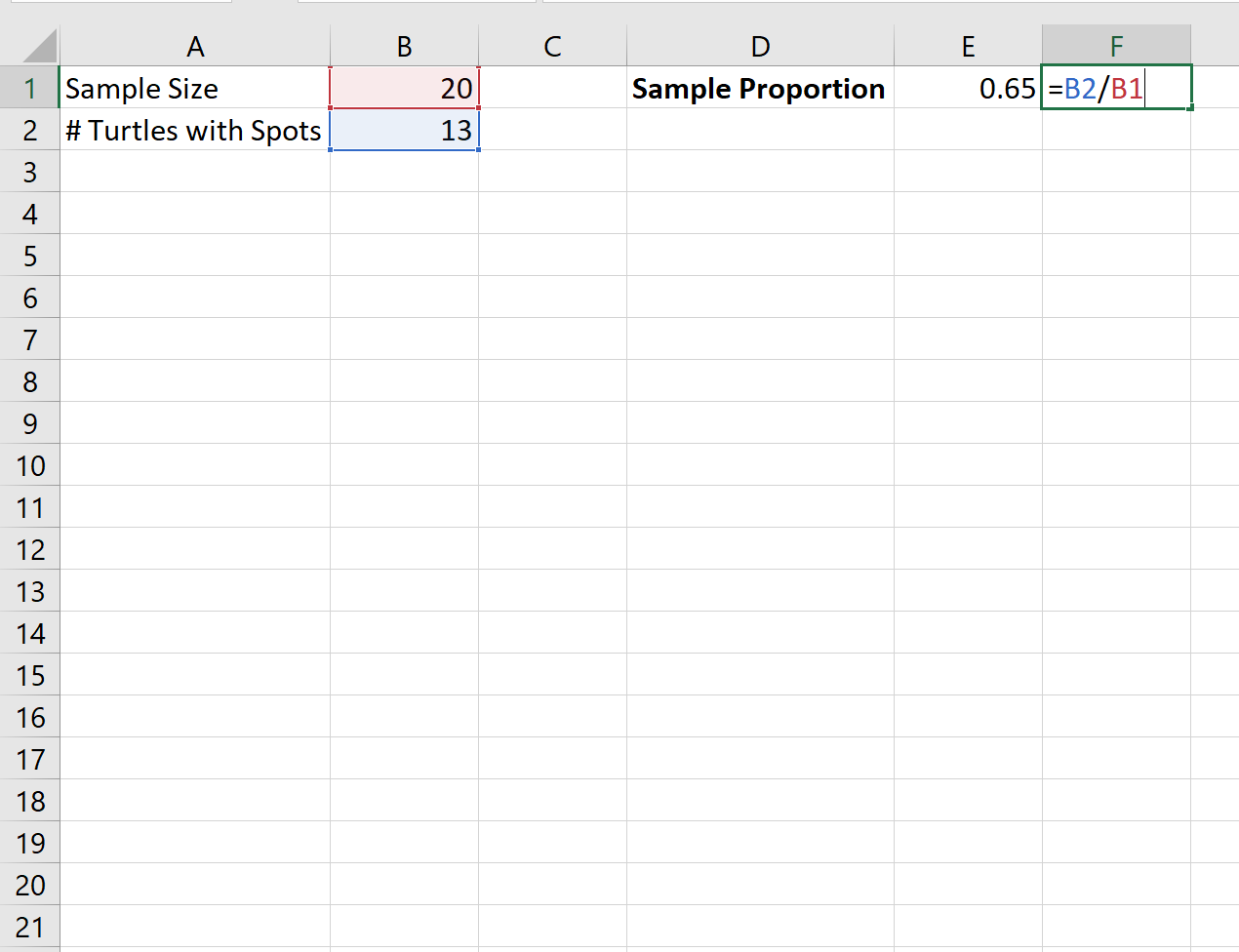
Daha sonra nüfus oranı için %95 güven aralığını hesaplamak üzere aşağıdaki formülü kullanabiliriz:
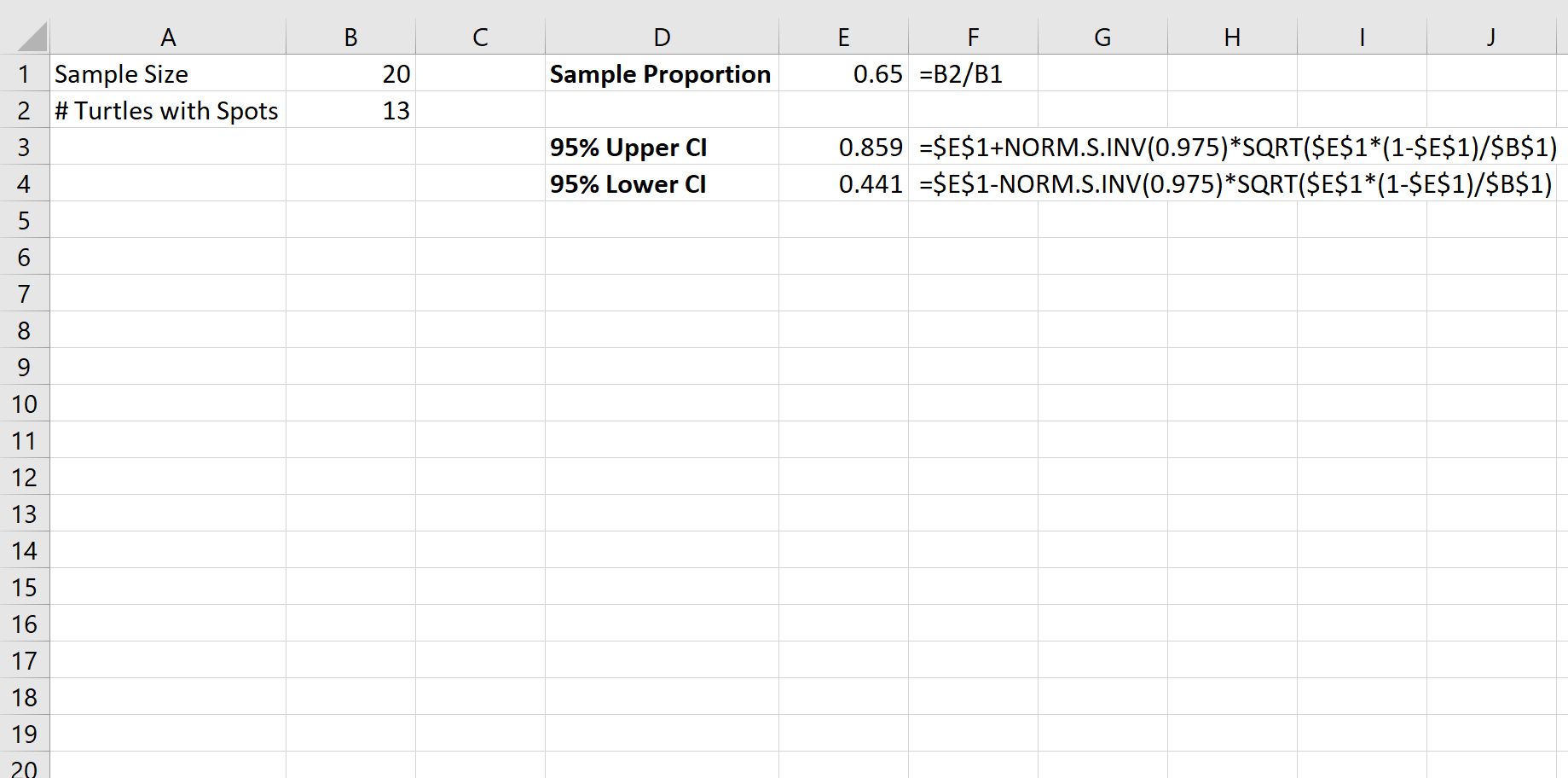
Bu popülasyondaki benekli kaplumbağaların gerçek oranının [0,44, 0,86] aralığında olduğundan %95 eminiz.
Oran hesaplayıcının güven aralığını kullanarak bu sonuçları doğrulayabiliriz.
Ek kaynaklar
Excel’de Güven Aralıkları Nasıl Hesaplanır?
Excel’de bir tahmin aralığı nasıl hesaplanır
Excel’de hata payı nasıl hesaplanır
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil