Normal dağılım

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makale istatistikte normal dağılımın ne olduğunu açıklamaktadır. Böylece normal dağılımın tanımını, normal dağılım örneklerini ve normal dağılımın özelliklerinin neler olduğunu bulacaksınız.

Normal dağılım nedir?

Normal dağılım, grafiği çan şeklinde ve ortalamasına göre simetrik olan sürekli bir olasılık dağılımıdır. İstatistikte normal dağılım çok farklı özelliklere sahip olguları modellemek için kullanılır, bu nedenle bu dağılım çok önemlidir.

Aslında istatistikte normal dağılım, tüm olasılık dağılımları arasında açık ara en önemli dağılım olarak kabul edilir, çünkü sadece çok sayıda gerçek dünya olayını modellemekle kalmaz, aynı zamanda normal dağılım diğer olasılık türlerine yaklaşık olarak da kullanılabilir. dağıtımlar. belirli koşullar altında.

Normal dağılımın sembolü büyük harf N’dir. Yani bir değişkenin normal dağılım izlediğini belirtmek için N harfi ile gösterilir ve parantez içinde aritmetik ortalaması ve standart sapması değerleri eklenir.

$X\sim N(\mu,\sigma)$

Normal dağılımın Gauss dağılımı , Gauss dağılımı ve Laplace-Gauss dağılımı dahil olmak üzere birçok farklı adı vardır.

Normal Dağılım Örnekleri

Tipik olarak normal bir dağılım izleyen veri kümeleri çok sayıda gözlem içerir ve çok genel konuları kapsar. Aşağıda genellikle normal dağılımla modellenebilecek istatistiksel örneklerin birkaç örneği verilmiştir.

Normal dağılım örnekleri:

Bir kurstaki öğrencilerin büyüklüğü.
Bir şirketin çalışanlarının IQ’su.
Bir fabrikada bir günde üretilen hatalı parça sayısı.
Öğrencilerin bir derste yaptıkları sınavda aldıkları notlar.
Borsada işlem gören şirketlerin hisselerinin karlılığı.

Normal dağılım grafiği

Normal dağılımın ne olduğunu ve bu tür olasılık dağılımının bazı örneklerini gördükten sonra, kavramı daha iyi anlamak için grafiğinin nasıl göründüğüne bakalım.

Aşağıdaki grafikte normal dağılımın yoğunluk fonksiyonunun aritmetik ortalama ve standart sapma değerlerine bağlı olarak nasıl değiştiğini görebilirsiniz.

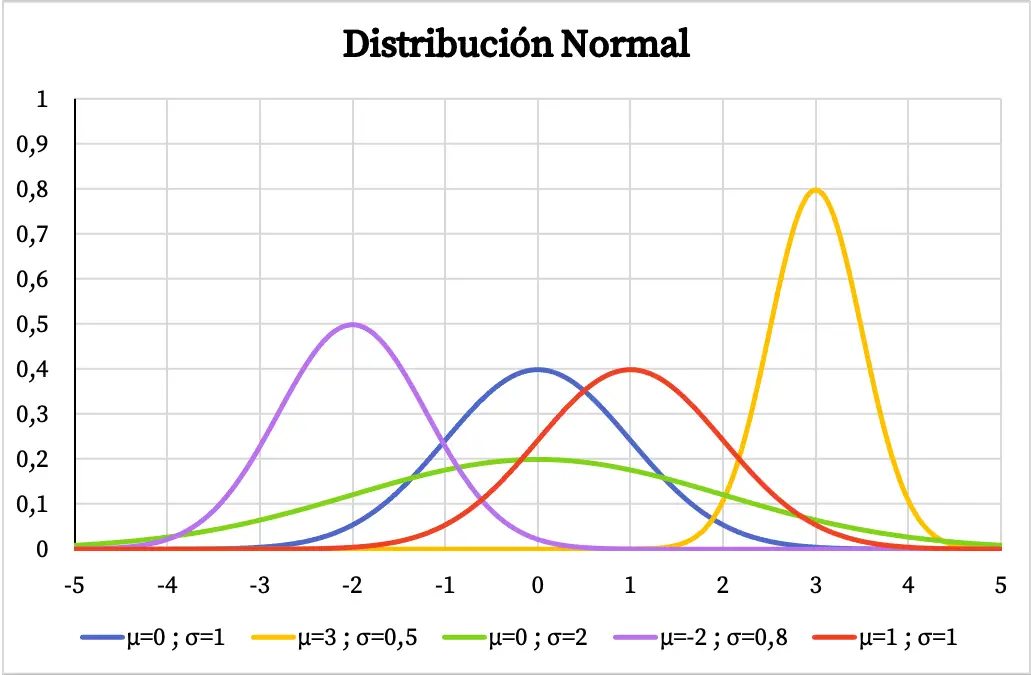
Aritmetik ortalamayı merkeze alan çan şekline sahip bir değişkenin normal dağılıma sahip olması, en çok tekrarlanan değerin ortalama olduğu ve ortalamanın etrafındaki değerlerin uç değerlerden daha sık tekrarlandığı anlamına gelir. Benzer şekilde, normal dağılımın standart sapması ne kadar büyük olursa, grafiksel temsilinin şekli de o kadar düz olur.

Öte yandan normal dağılımın kümülatif olasılık fonksiyonunun grafiği de aşağıdaki görselde görebileceğiniz gibi aritmetik ortalama ve standart sapma değerlerine bağlıdır:

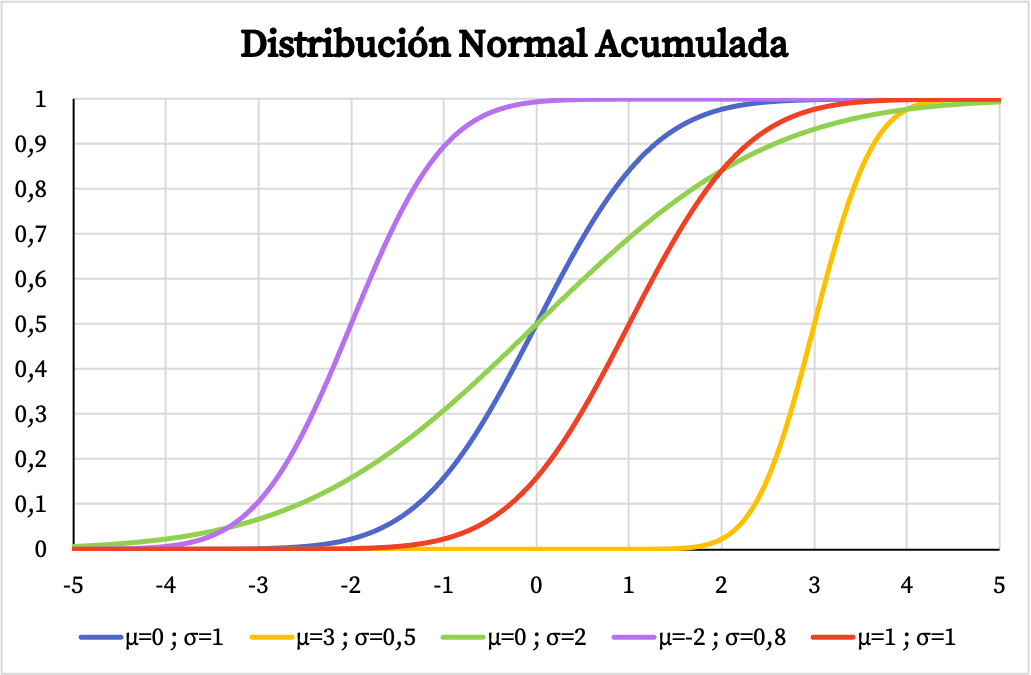
Normal dağılımın yoğunluk fonksiyonu ve dağılım fonksiyonu, bu dağılıma bağlı olasılıkların hesaplanmasını mümkün kılar. Ancak onların formüllerini kullanmak yerine doğrudan normal dağılım tablolarını kullanabilirsiniz çünkü daha hızlıdır. Bu tablolara aşağıdaki bağlantıdan ulaşabilirsiniz:

➤ Bakınız: Normal dağılım tablosu

Normal dağılımın özellikleri

Normal dağılım aşağıdaki özelliklere sahiptir:

Normal dağılım, aritmetik ortalaması (μ) ve standart sapması (σ) olmak üzere iki karakteristik parametreye bağlıdır.

$X\sim N(\mu,\sigma)$

Normal dağılım pozitif ve negatif değerler alabilir, dolayısıyla normal dağılımın alanı gerçek sayılardan oluşur.

$x\in \mathbb{R}$

Normal dağılımın medyanı ve modu, dağılımın aritmetik ortalamasına eşittir.

$Me=Mo=\mu$

Normal dağılımın çarpıklık katsayısı ve basıklık katsayısı sıfırdır.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

Normal dağılımın yoğunluk fonksiyonunun formülü şöyledir:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Benzer şekilde normal dağılımın kümülatif olasılık fonksiyonu formülü şöyledir:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Merkezi limit teoreminin bir uygulaması, λ değeri yeterince büyük olduğunda bir Poisson dağılımının normal dağılıma yaklaşabilmesidir.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Merkezi limit teoreminin başka bir uygulaması, çok sayıda gözlem içeren veri kümeleri için binom dağılımının normal dağılımla yaklaşık olarak tahmin edilebilmesidir.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Standart normal dağılım

Birim normal dağılım olarak da adlandırılan standart normal dağılım , normal dağılımın en basit halidir. Daha doğrusu standart normal dağılım, ortalama ve standart sapma değerleri sırasıyla 0 ve 1’e eşit olan bir normal dağılımdır.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Herhangi bir normal dağılımın, her bir değerden aritmetik ortalamasının çıkarılmasını ve ardından standart sapmaya bölünmesini içeren, yazma adı verilen bir işlem uygulanarak standart normal dağılıma dönüştürülebileceğini unutmayın.

Ek olarak standart normal dağılım, olasılık tablosunu kullanarak normal dağılımın herhangi bir olasılığını belirlemek için kullanılır. Dolayısıyla normal dağılım olasılığını bulmak için önce değişkeni standart normal dağılıma dönüştürmek üzere giriyoruz ve ardından karşılık gelen olasılık değerinin ne olduğunu görmek için tabloya bakıyoruz. Daha fazlasını öğrenmek için aşağıdaki bağlantıya tıklayın:

➤ Bakınız: Standart Normal Dağılım

Normal dağılım ve ampirik kural

İstatistikte, 68-95-99,7 kuralı olarak da adlandırılan temel kural , normal dağılımdaki ortalamanın üç standart sapması dahilinde kalan değerlerin yüzdesini tanımlayan bir kuraldır.

Daha spesifik olarak, temel kural aşağıdakileri belirtir:

Normal dağılımdaki değerlerin %68’i ortalamanın bir standart sapması içerisinde yer alır.
Normal dağılımdaki değerlerin %95’i ortalamanın iki standart sapması içerisinde yer alır.
Normal dağılımdaki değerlerin %99,7’si ortalamanın üç standart sapması dahilindedir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil