Normal dağılım

Normal dağılım istatistikte en yaygın olasılık dağılımıdır.

Normal dağılımlar aşağıdaki özelliklere sahiptir:

• Çan şekli
• Simetrik
• Ortalama ve medyan eşittir; her ikisi de dağıtımın merkezinde yer alır
• Verilerin yaklaşık %68’i ortalamanın bir standart sapması dahilindedir
• Verilerin yaklaşık %95’i ortalamanın iki standart sapması dahilindedir.
• Verilerin yaklaşık %99,7’si ortalamanın üç standart sapması dahilindedir.

Son üç nokta, bazen 68-95-99,7 kuralı olarak da adlandırılan temel kural olarak bilinir.

İlgili: Temel Kurallar (Uygulama Konuları)

Normal bir eğri nasıl çizilir

Normal bir eğri çizmek için ortalamayı ve standart sapmayı bilmemiz gerekir.

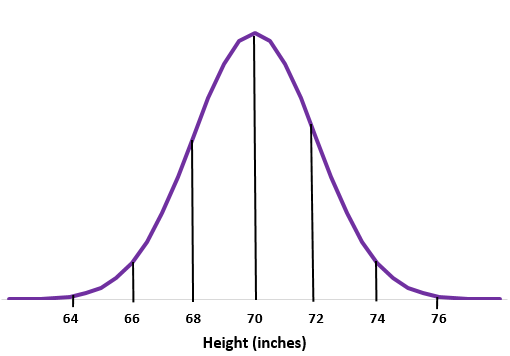
Örnek 1: Belirli bir okuldaki erkeklerin boyunun ortalama $\mu =\; 70\; inç\; ve$ standart sapmanın $\sigma \; =\; 2\; inç\; olacak\; şekilde\; normal\; şekilde\; dağıldığını\; varsayalım.\; Normal\; eğriyi\; çizin.$

Adım 1: Normal bir eğri çizin.

Adım 2: Ortalama 70 inç ortadadır.

Adım 3: Her standart sapma 2 inçlik bir mesafeye karşılık gelir.

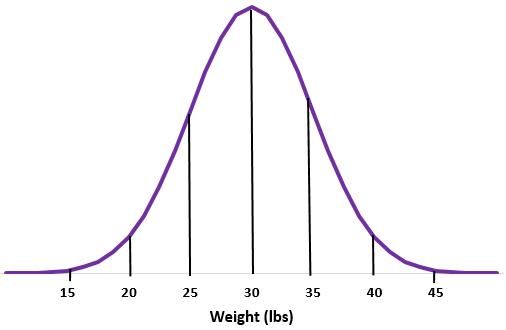
Örnek 2: Belirli bir su samuru türünün ağırlığının $\mu =\; 30\; lb\; ortalaması\; ve$ $\sigma \; =\; 5\; lb$ standart sapması ile normal şekilde dağıldığını varsayalım. $Normal\; eğriyi\; çizin.$

Adım 1: Normal bir eğri çizin.

Adım 2: 30 kiloluk ortalama ortada düşer.

Adım 3: Her standart sapma 5 lbs’lik bir mesafeye karşılık gelir

Normal Dağılım Kullanılarak Yüzdeler Nasıl Bulunur?

Bazen 68-95-99,7 kuralı olarak da adlandırılan temel kural , normal dağılım gösteren bir rastgele değişken için verilerin %68’inin ortalamadan bir standart sapma aralığına, %95’inin ise iki standart sapma aralığına düştüğünü belirtir. ortalamadan sapmalar ve %99,7’si ortalamadan üç standart sapma dahilindedir.

Bu kuralı kullanarak yüzdelerle ilgili soruları cevaplayabiliriz.

Örnek: Belirli bir okuldaki erkeklerin boyunun ortalama $\mu =\; 70\; inç\; ve$ standart sapmanın $\sigma \; =\; 2\; inç\; olacak\; şekilde\; normal\; şekilde\; dağıldığını\; varsayalım.$

$Bu\; okuldaki\; erkeklerin\; yaklaşık\; yüzde\; kaçı\; 74\; inçten\; uzun?$

Çözüm:

Adım 1: Ortalaması $\mu =\; 70\; inç\; ve$ standart sapması $\sigma \; =\; 2\; inç\; olan\; bir\; normal\; dağılım\; çizin.$

Adım 2: 74 inçlik bir yükseklik, ortalamanın iki standart sapma üzerindedir. Bu noktanın üzerindeki yüzdeleri normal dağılıma ekleyin.

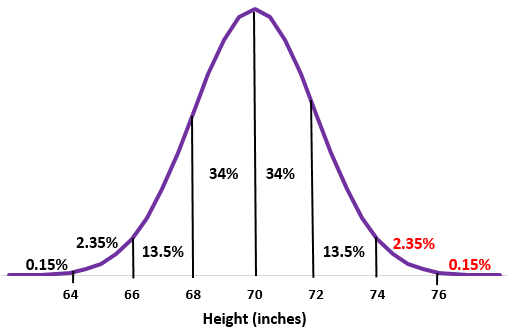
%2,35 + %0,15 = %2,5

Bu okuldaki erkeklerin yaklaşık %2,5’inin boyu 74 inçten fazladır.

$Bu\; okuldaki\; erkeklerin\; yaklaşık\; yüzde\; kaçının\; boyu\; 68\; inç\; ila\; 72\; inç\; arasındadır?$

Çözüm:

Adım 1: Ortalaması $\mu =\; 70\; inç\; ve$ standart sapması $\sigma \; =\; 2\; inç\; olan\; bir\; normal\; dağılım\; çizin.$

Adım 2: 68 inç ve 72 inçlik yükseklik sırasıyla ortalamanın altında ve üstünde bir standart sapmadır. Normal dağılımdaki bu iki nokta arasındaki yüzdeleri toplamanız yeterlidir.

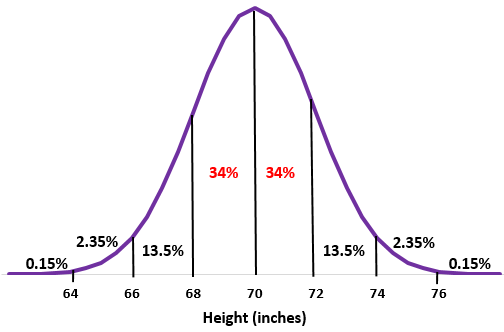
%34 + %34 = %68

Bu okuldaki erkeklerin yaklaşık %68’inin boyu 68 inç ila 72 inç arasındadır.

Normal dağılım kullanılarak sayımlar nasıl bulunur?

Sayımlarla ilgili soruları yanıtlamak için de temel kuralı kullanabiliriz.

Örnek: Belirli bir su samuru türünün ağırlığının $\mu =\; 30\; lb\; ortalaması\; ve$ $\sigma \; =\; 5\; lb$ standart sapması ile normal şekilde dağıldığını varsayalım.

Belirli bir kolonide bu su samurlarından 200 adet bulunmaktadır. Bu su samurularından yaklaşık kaç tanesinin ağırlığı 35 poundun üzerindedir?

Çözüm:

Adım 1: Ortalaması $\mu =\; 30\; lb\; ve$ standart sapması $\sigma \; =\; 5\; lb$ olan bir normal dağılım çizin.

Adım 2: 35 lbs’lik bir ağırlık, ortalamanın üzerinde bir standart sapmadır. Bu noktanın üzerindeki yüzdeleri normal dağılıma ekleyin.

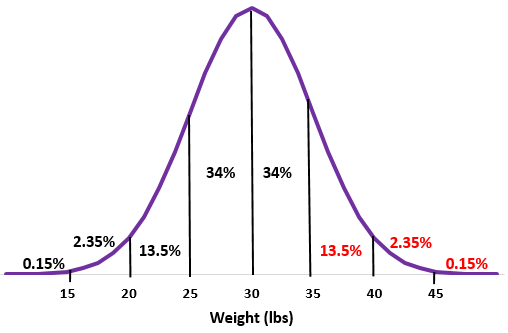
%13,5 + %2,35 + %0,15 = %16

Adım 3: Kolonide 200 su samuru olduğundan, 200’ün %16’sı = 0,16 * 200 = 32

Bu kolonideki yaklaşık 32 su samuru 35 poundun üzerindedir.

Bu kolonide yaklaşık olarak kaç su samuru 30 poundun altındadır?

Yukarıda attığımız tüm adımları takip etmek yerine, normal dağılımın medyanının ortalamaya eşit olduğunu, yani bu durumda 30 pound olduğunu fark edebiliriz.

Bu, su samurularının yarısının 30 pounddan fazla, diğer yarısının ise 30 pounddan az olduğu anlamına gelir. Bu, 200 su samuru’nun %50’sinin 30 pound’dan daha hafif olduğu anlamına gelir; yani 0,5 * 200 = 100 su samuru .

Ek kaynaklar

Aşağıdaki eğitimler normal dağılım hakkında ek bilgi sağlar:

Normal dağılımın 6 somut örneği
Normal dağılım ve t dağılımı: fark
Excel’de Çan Eğrisi Nasıl Oluşturulur
Python’da Çan Eğrisi Nasıl Oluşturulur