Normal dağılım ve t dağılımı: fark nedir?

Normal dağılım tüm istatistiklerde en sık kullanılan dağılımdır ve simetrik ve çan şeklinde olduğu bilinmektedir.

Yakından ilişkili bir dağılım da simetrik ve çan şeklinde olan ancak normal dağılımdan daha ağır “kuyruklara” sahip olan t dağılımıdır .

Başka bir deyişle, normal dağılıma göre dağılımda daha fazla değer merkeze göre uçlarda yer alır:

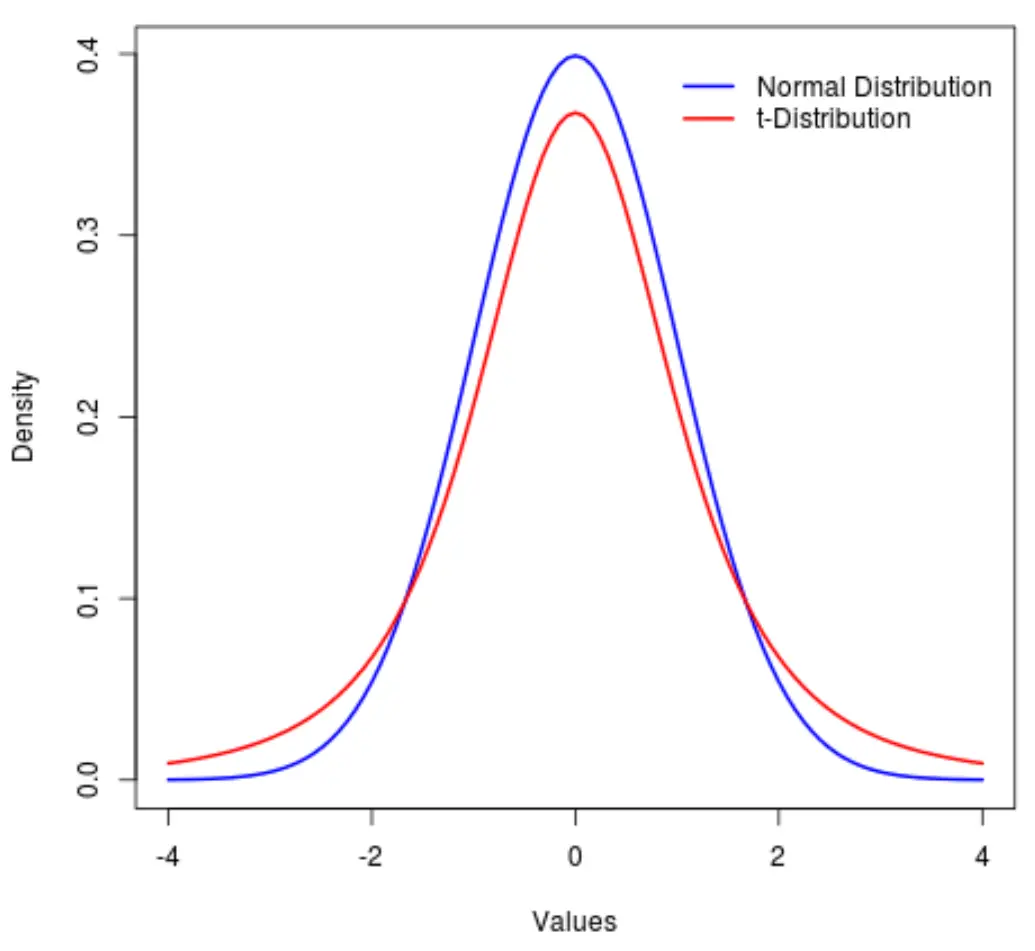
İstatistik jargonunda, bir dağılımın ne kadar “ağır” olduğunu ölçmek için basıklık adı verilen bir ölçüm kullanırız. Dolayısıyla, bir t dağılımının basıklığının normal dağılımdan daha büyük olduğunu söyleyebiliriz.

Uygulamada, hipotez testi yaparken veyagüven aralıkları oluştururken çoğunlukla t dağılımını kullanırız.

Örneğin, popülasyon ortalaması için güven aralığını hesaplama formülü şöyledir:

Güven aralığı = x +/- t _{1-α/2, n-1} *(s/√ n )

Altın:

• x : örnek ortalama
• t: anlamlılık düzeyi α ve örneklem büyüklüğü n’ye dayalı olarak kritik t değeri
• s: numune standart sapması
• n: örneklem büyüklüğü

Bu formülde, aşağıdaki koşullardan biri doğru olduğunda z tablosunun kritik değeri yerine t tablosunun kritik değerini kullanırız:

• Popülasyon standart sapmasını bilmiyoruz.
• Örneklem büyüklüğü 30’dan küçük veya ona eşittir.

Aşağıdaki akış şeması, kritik değeri tablo t’den mi yoksa tablo z’den mi kullanmanız gerektiğini bilmenin yararlı bir yolunu sağlar:

Güven aralıklarını oluştururken t dağılımını kullanmak ile normal dağılımı kullanmak arasındaki temel fark, t dağılımının kritik değerlerinin daha büyük olacağı ve dolayısıyla daha geniş güven aralıklarına yol açacağıdır.

Örneğin, aşağıdaki bilgilerle rastgele bir kaplumbağa örneği toplamak amacıyla bir kaplumbağa popülasyonunun ortalama ağırlığı için %95’lik bir güven aralığı oluşturmak istediğimizi varsayalım:

• Örneklem büyüklüğü n = 25
• Ortalama numune ağırlığı x = 300
• Örneklem standart sapması s = 18,5

%95 güven düzeyi için kritik z değeri 1,96 iken df = 25-1 = 24 serbestlik derecesi ile %95 güven aralığı için kritik t değeri 2,0639’dur .

Dolayısıyla, z-kritik değeri kullanılarak popülasyon ortalaması için %95 güven aralığı şöyledir:

%95 GA = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Popülasyon ortalaması için %95 güven aralığı t-kritik değeri kullanıldığında şu şekildedir:

%95 GA = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

T-kritik değeri ile güven aralığının daha geniş olduğuna dikkat edin.

Buradaki fikir, küçük örneklem boyutlarına sahip olduğumuzda, gerçek popülasyon ortalamasından daha az emin olduğumuz, bu nedenle, gerçek popülasyon ortalamasını içerme şansı daha fazla olan daha geniş güven aralıkları üretmek için t dağılımını kullanmanın yararlı olduğudur.

T dağılımı için serbestlik derecelerinin görselleştirilmesi

Serbestlik derecesi arttıkça t dağılımının normal dağılıma yaklaştığını belirtmek gerekir.

Bunu göstermek için, t dağılımının şeklini aşağıdaki serbestlik dereceleriyle gösteren aşağıdaki grafiği düşünün:

• sd = 3
• sd = 10
• sd = 30

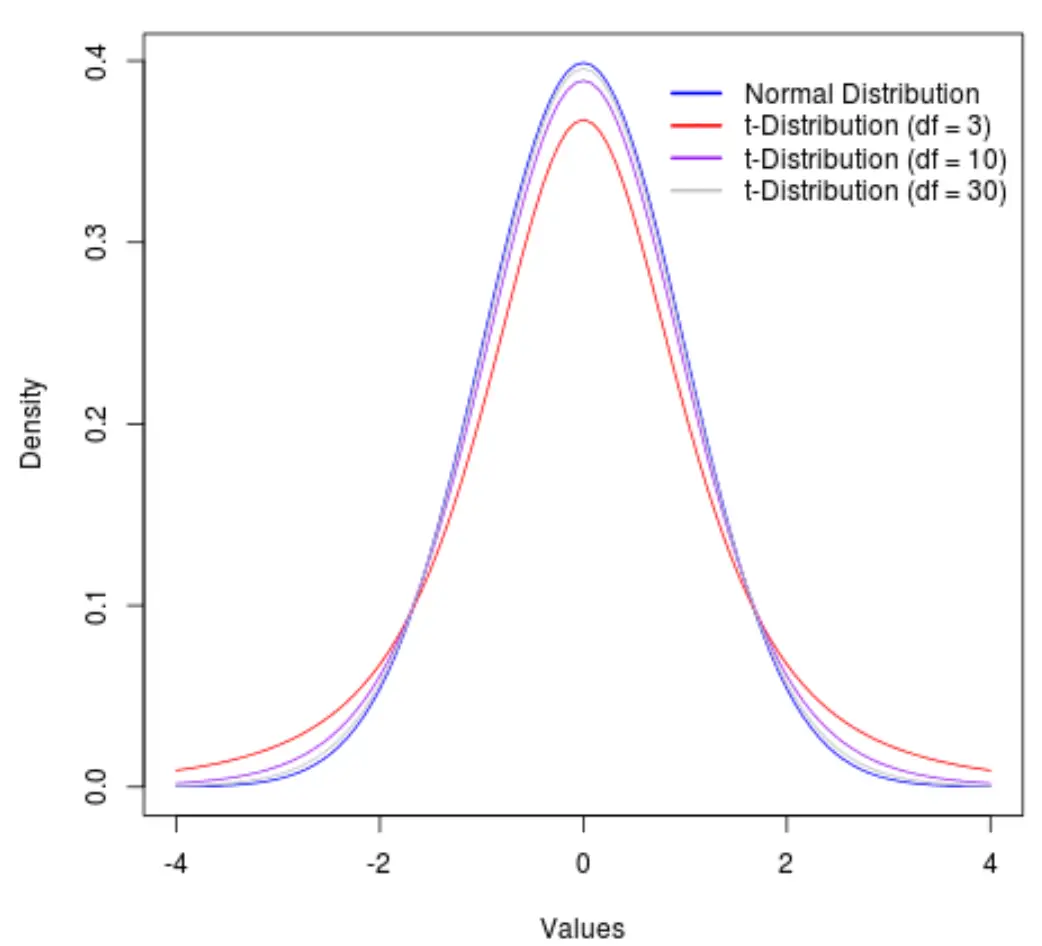
30 serbestlik derecesinin ötesinde, t dağılımı ve normal dağılım o kadar benzer hale gelir ki, formüllerde t-kritik değeri ile z-kritik değeri kullanımı arasındaki farklar ihmal edilebilir hale gelir.