Standart normal dağılım

İle Dr.benjamin anderson Ağustos 4, 2023 Olasılık 0 Yorum

Bu makalede standart normal dağılımın ne olduğu ve ne için kullanıldığı açıklanmaktadır. Ayrıca standart normal dağılımın özelliklerini, karakteristik değerlerini içeren tabloyu ve ayrıca çözülmüş bir alıştırmayı bulacaksınız.

Standart normal dağılım nedir?

Birim normal dağılım olarak da adlandırılan standart normal dağılım , normal dağılımın en basit halidir. Daha doğrusu standart normal dağılım, ortalama ve standart sapma değerleri sırasıyla 0 ve 1’e eşit olan bir normal dağılımdır.

Bu nedenle standart normal dağılım N(0,1) olarak tanımlanır; burada birinci parametre dağılımın ortalaması, ikinci parametre ise standart sapmasıdır (veya SD).

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Standart normal dağılımın grafiği bu nedenle aşağıdaki gibidir:

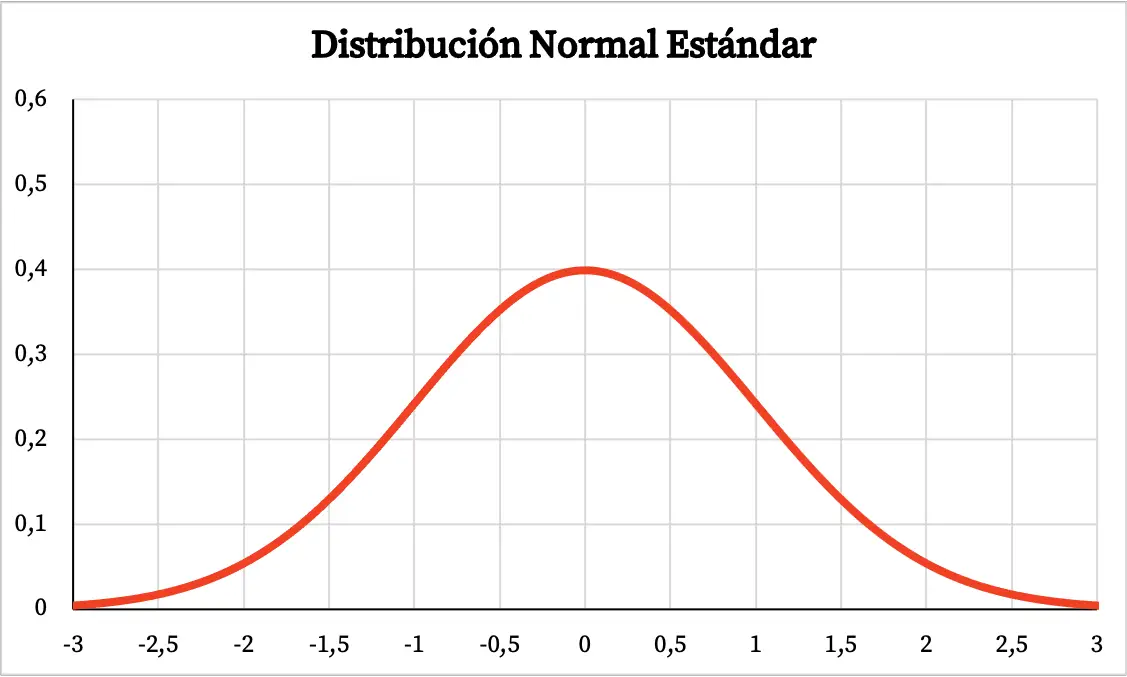
Standart normal dağılım formülü

Herhangi bir normal dağılımı standart normal dağılıma dönüştürmek için normal dağılımın ortalamasını tüm değerlerinden çıkarmanız ve ardından normal dağılımın standart sapmasına bölmeniz gerekir.

Standart normal dağılım formülü bu nedenle aşağıdaki gibidir:

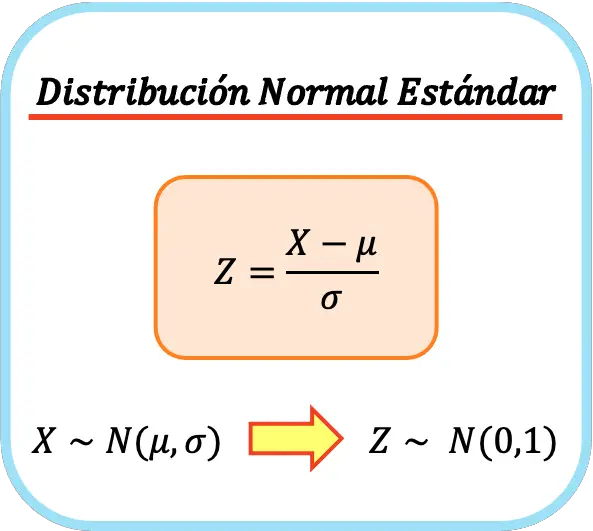
Bu sayede yeni değişkenin aritmetik ortalaması ve standart sapması sırasıyla 0 ve 1 olacağından standart normal dağılım elde etmiş oluruz. Bu işleme aynı zamanda tek değişkenli normalizasyon veya tek değişkenli normalizasyon da denir.

Standart normal dağılım tablosu

Standart normal dağılım tablosu, gözlemlenen bir değerin standart normal dağılımın belirli bir değerinden küçük olma olasılıklarını içeren bir tablodur.

Ek olarak, normal dağılımın işlevi ortalamasına ve standart sapmasına bağlı olduğundan, herhangi bir normal dağılımın olasılıklarını belirlemek için standart normal dağılım tablosu da kullanılır. Bunu yapmak için normal dağılım standart normal dağılıma yazılır ve ardından tabloya hangi olasılığın buna karşılık geldiğine bakarız.

Yani standart normal dağılım tablosundaki değerler şu şekildedir:

Standart Normal Dağılım Örneği

Artık standart normal dağılımın tanımını ve formülünü bildiğimize göre, kavramı daha iyi anlamak için aşağıda somut bir örnek vereceğiz.

Sürekli bir rastgele değişken, ortalaması 45 ve standart sapması 15 olan normal bir dağılım izlemektedir; 58’den küçük veya buna eşit bir değer elde etme olasılığı nedir?

$N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}$

Normal dağılım olasılığını bulmak için özellik tablosunu kullanmamız gerekir ancak bunu yapabilmek için öncelikle standart normal dağılım elde edecek şekilde yazma işlemini yapmamız gerekir. Bu nedenle standart normal dağılım formülünü kullanıyoruz:

$Z=\cfrac{X-\mu}{\sigma}$

Yani ortalamayı olasılık değerinden çıkarıyoruz ve sonra standart sapmaya bölüyoruz

$\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]$

Değişkeni standartlaştırdıktan sonra, 0,87 değerinin hangi olasılığa karşılık geldiğini görmek için standart normal dağılım olasılık tablosuna gideriz (yukarıya bakın):

$\displaystyle P[Z\leq 0,87]=0,8078$

Dolayısıyla 58’e eşit veya daha küçük bir değer elde etme olasılığı %80,78’dir.

Standart normal dağılımın özellikleri

Standart normal dağılım aşağıdaki özelliklere sahiptir:

Standart normal dağılım 0 merkezli simetrik bir dağılımdır.
Normal dağılım gibi, standart normal dağılım grafiği de çan şeklindedir ve grafik alanının çoğu ortalamanın etrafında düşer.
Bu nedenle normal dağılımın ortalaması, modu ve medyanı aynı değere yani 0’a sahiptir.
Standart normal dağılımın maksimumu z=0’dadır.
Benzer şekilde, standart normal dağılımın z=-1 ve z=+1 olmak üzere iki dönüm noktası vardır.
Temel kurala göre, değerlerin %68’inin +1 ile -1 arasındaki standart normal dağılıma, %95’inin +2 ile -2 arasındaki değerlerin ve %99,7’sinin +1 ile -2 arasındaki standart normal dağılıma düştüğünü biliyoruz. 3 ve – 3.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil