Nüfus anlamına gelir

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makale istatistikte nüfusun ne anlama geldiğini açıklamaktadır. Aynı şekilde popülasyon ortalaması formülünün ne olduğunu, popülasyon ortalamasının güven aralığının nasıl hesaplandığını ve ayrıca popülasyon ortalaması ile ‘örneklem’ ortalaması arasındaki farkın ne olduğunu öğreneceksiniz.

Nüfus ortalaması nedir?

Nüfus ortalaması, istatistiksel popülasyonun tüm öğelerinin aritmetik ortalamasıdır. Bu nedenle popülasyon ortalamasını hesaplamak için tüm popülasyon değerlerinin toplanması ve ardından popülasyondaki toplam element sayısına bölünmesi gerekir.

Popülasyon ortalamasının sembolü Yunanca μ harfidir.

Benzer şekilde popülasyon ortalaması da bir popülasyonu temsil eden değişkenin beklenen değeri olarak tanımlanabilir.

Nüfus ortalaması nasıl hesaplanır

Nüfus ortalamasının tanımını gördükten sonra, anlamını daha iyi anlamak için nüfus ortalamasının nasıl hesaplandığına bakalım.

İstatistiksel popülasyondaki tüm değerler biliniyorsa, popülasyon ortalamasını hesaplamak için aritmetik ortalama formülü basitçe uygulanmalıdır. Yani bu durumda nüfus ortalamasını hesaplamak için tüm nüfus değerlerini toplayıp ardından toplam veri sayısına bölmemiz gerekiyor.

Dolayısıyla, popülasyonun tüm unsurlarının değerini biliyorsak, popülasyon ortalamasını hesaplama formülü aşağıdaki gibidir:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Bakınız: Aritmetik ortalamayı hesaplama örneği

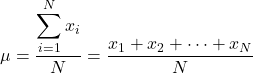
Ancak genel olarak tüm popülasyon değerleri bilinmediğinden, normalde popülasyon ortalamasının değeri aralıklarla tahmin edilir .

Nüfus ortalaması için güven aralığı

Uygulamada, bir popülasyondaki tüm bireyleri incelemek imkansızdır, bu nedenle normal olarak popülasyonun rastgele bir örneği seçilir ve bu örneklemin değerlerine dayalı olarak popülasyon ortalamasının değerinin bir tahmini yapılır. Daha kesin olarak, tüm popülasyonun ortalamasının büyük olasılıkla bulunacağı bir aralık hesaplıyoruz; bu aralığa popülasyon ortalamasının güven aralığı denir.

Popülasyon ortalaması için güven aralığı, Z _α/2 değerinin standart sapma (σ) ile çarpılması ve numune yüksekliğinin (n) kareköküne bölünmesiyle numune ortalamasından toplanıp çıkarılarak hesaplanır. Bu nedenle popülasyon ortalaması için güven aralığını hesaplama formülü şöyledir:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

Popülasyon varyansı bilindiğinde yukarıdaki formül kullanılır. Bununla birlikte, en yaygın durum olan popülasyon varyansı bilinmiyorsa, ortalamanın güven aralığı aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Altın:

$\overline{x}$

örnek anlamına gelir.
$t_{\alpha/2}$

α/2 olasılıkla n-1 serbestlik derecesinin Öğrenci t dağılımının değeridir. Büyük örneklem büyüklükleri ve %95 güven düzeyi için genellikle 1,96’ya, %99 güven düzeyi için ise genellikle 2,576’ya yakındır.
$s$

örnek standart sapmasıdır.
$n$

örneklem büyüklüğüdür.

➤ Bakınız: Popülasyon ortalaması için güven aralığını hesaplama örneği

Nüfus ortalaması ve örnek ortalaması

Son olarak, özet olarak, bu iki istatistiksel kavramın net olması için popülasyon ortalaması ile örnek ortalaması arasındaki farkları gözden geçireceğiz.

Popülasyon ortalaması ile örnek ortalaması arasındaki fark, ortalamanın hesaplandığı değer aralığıdır. Popülasyon ortalaması tüm istatistiksel popülasyonun ortalamasıdır, örnek ortalaması ise popülasyonun bir örneğinin ortalamasıdır.

Ayrıca popülasyon ortalamasını örnek ortalamasından ayırt etmek için farklı sembollerle temsil edilirler. Nüfus anlamına gelen sembol

$\mu$

, diğer taraftan, örnek ortalamanın sembolü

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Bu iki ortalama türü arasındaki farklar konusunda hâlâ şüpheleriniz varsa veya örneklem ortalamasının hesaplanması hakkında daha fazla bilgi edinmek istiyorsanız aşağıdaki makaleye başvurabilirsiniz:

➤ Bakınız: Örnek ne anlama geliyor?

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil