Örnek oranı
Bu makale istatistikte örneklem oranının ne olduğunu açıklamaktadır. Böylece örnek oranının nasıl hesaplanacağını, çözülmüş bir alıştırmayı ve ayrıca örnek oranı ile nüfus oranı arasındaki farkın ne olduğunu keşfedeceksiniz.
Örnek oranı nedir?
Örnek oranı, bir örneklemdeki başarılı vakaların örneklem büyüklüğüne oranıdır. Bu nedenle örneklem oranını hesaplamak için örneklemdeki başarı sayısının toplam veri sayısına bölünmesi gerekir.
Numune oranının sembolü
![]()
.
İstatistiklerde, bir anket yürütülürken genellikle nüfus verilerinin tamamı bilinmez; bu nedenle genellikle temsili bir örnek üzerinde çalışma yapılır ve daha sonra çıkarılan sonuçlar tüm nüfusa yansıtılır. nüfus. Bu nedenle, örneklem oranı tüm popülasyonun oranını tahmin etmek için kullanılır. Aşağıda bunun nasıl yapıldığını göreceğiz.
Oran Formülü Örneği
Örnek oranı, örnekteki başarılı vaka sayısının örneklem büyüklüğüne bölünmesine eşittir. Bu nedenle numune oranını hesaplama formülü şöyledir:
![]()
Altın:
-

örnek oranıdır.
-

örnekteki başarılı vakaların sayısıdır.
-

örnekteki veri öğelerinin toplam sayısıdır.
Örnek Oran Hesaplama Örneği
Bu bölümde örnek oranın tanımını ve formülünün ne olduğunu gördükten sonra örnek oranın nasıl hesaplandığını görebilmeniz için basit bir örnek çözeceğiz.
- Bir firma bir oyuncak üretiyor ve onun bir parçasını dışarıdan başka bir firmadan satın alıyor. Ancak satın aldığı partiler içerisinde hatalı parçalar ortaya çıktığından, iyi durumdaki parçaların oranını ve kusurlu parçaların oranını bulmak için istatistiksel bir çalışma yapmaya karar verir. Yani 1000 adetlik bir numune sipariş ediyorsunuz ve 138 adet hatalı parça buluyorsunuz. Numunedeki iyi durumdaki parçaların oranı nedir? Peki numunedeki kusurlu parçaların oranı nedir?
Numunedeki hasarsız parçaların sayısı 1000 eksi kusurlu parçaların sayısıdır:
![]()
Örnek oranını bulmak için yukarıda gördüğümüz formülü uyguluyoruz:
![]()
Dolayısıyla iyi durumdaki parça örneklerinin oranı %86,2’dir.
Öte yandan, kusurlu parçaların oranı, bir eksi iyi parçaların oranına eşittir:
![]()
Bu nedenle kusurlu parçaların örnek oranı %13,8’dir.
Örnek oranı ve popülasyon oranı
Nüfus oranı istatistiksel nüfusun oranıdır. Yani nüfus oranı, incelenen bir popülasyonun başarı durumlarının söz konusu popülasyonun parçası olan tüm unsurlarla ilişkisidir.
Bu nedenle, ulusal oran ile nüfus oranı arasındaki fark, ulusal oranın çoğunluğun vakalarının oranı olmasıdır; değişimde nüfus oranı, Nüfusun tüm unsurlarına ilişkin olayların vakalarının oranını ifade etmektedir.
Örnek oranını nüfus oranından ayırmak için farklı sembollerle temsil edilirler. Numune oranının sembolü
![]()
nüfus oranının simgesi ise
![]()
.
Genelde tüm nüfus değerleri bilinmediğinden nüfus oranı kesin olarak belirlenemez. Bunun yerine, nüfus oranının değeri genellikle aşağıdaki formülle bir güven aralığı kullanılarak tahmin edilir:
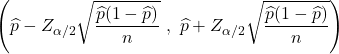
Nüfus oranının nasıl tahmin edildiğini görmek için aşağıdaki bağlantıya tıklayın:
Oranların örnekleme dağılımı
Son olarak, örnekleme oranıyla ilgili istatistiksel bir kavram olduğundan, oranların örnekleme dağılımının nelerden oluştuğunu göreceğiz.
Öncelikle örnekleme dağılımının ne olduğunu tanımlayarak başlayalım. Örnekleme dağılımı, istatistiksel bir popülasyondan olası tüm örneklerin dikkate alınmasından kaynaklanan dağılımdır.
Bu nedenle, orantıların örnekleme dağılımı , bir popülasyondaki olası her örneğin oranının hesaplanmasından kaynaklanan dağılımdır. Yani, bir popülasyondan olası tüm örnekleri incelersek ve örneklerin her birinin oranını hesaplarsak, hesaplanan değerler kümesi, örnek oranlarının örnekleme dağılımı olur.