Öğrencinin t dağılımı

İle Ağustos 4, 2023 Olasılık 0 Yorum

Bu makalede, Öğrenci t dağılımının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Ayrıca, Öğrenci t dağılımının grafiği ve bu tür olasılık dağılımının özelliklerinin neler olduğu gösterilmiştir.

Öğrenci dağılımı nedir?

Öğrenci t dağılımı istatistikte yaygın olarak kullanılan bir olasılık dağılımıdır. Özellikle, Öğrenci t dağılımı, iki numunenin ortalamaları arasındaki farkı belirlemek ve güven aralıklarını oluşturmak için Öğrenci t testinde kullanılır.

Öğrencinin t dağılımı, istatistikçi William Sealy Gosset tarafından 1908 yılında “Öğrenci” takma adı altında geliştirildi.

Öğrencinin t dağılımı, toplam gözlem sayısından bir birimin çıkarılmasıyla elde edilen serbestlik derecesi sayısıyla tanımlanır. Bu nedenle, Öğrenci t dağılımının serbestlik derecesini belirleme formülü ν=n-1’dir .

\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}

Öğrencinin t dağılım grafiği

Artık Öğrenci t dağılımının tanımını bildiğimize göre grafiğinin ne olduğuna bakalım. Aşağıda, farklı serbestlik derecelerine sahip Öğrenci t dağılımlarının birkaç örneğini grafiksel olarak görebilirsiniz.

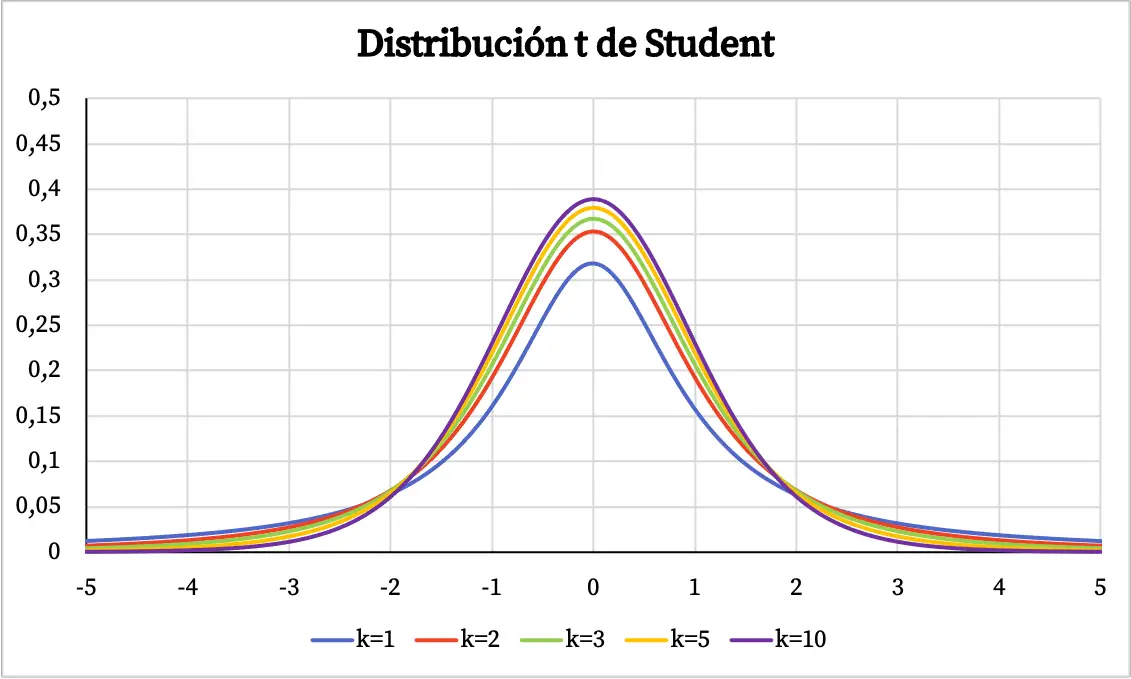
Öğrencinin t dağılım grafiği

Öğrenci t dağılımının grafiğinden aşağıdaki özellikler çıkarılabilir:

  • Öğrenci t dağılımı 0’da simetrik merkezlidir ve çan şeklindedir.
  • Öğrenci t dağılımı normal dağılıma göre daha dağınıktır, yani Öğrenci t dağılımının eğrisi daha geniştir.
  • Öğrencinin t dağılımının serbestlik derecesi ne kadar fazlaysa, dağılımı da o kadar düşük olur.

Yukarıdaki grafikte, Öğrenci t dağılımının yoğunluk fonksiyonu, serbestlik derecesine göre çizilmiştir. Ancak aşağıda Öğrenci t dağılımının kümülatif olasılık fonksiyonunun nasıl değiştiğini görebilirsiniz:

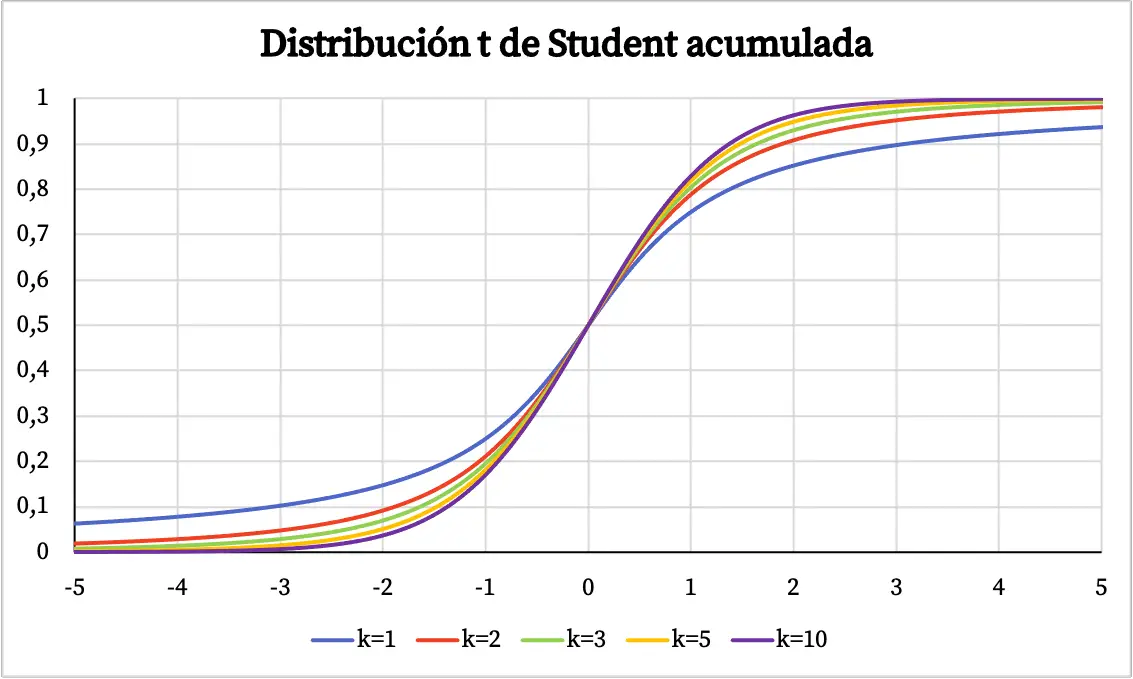
Öğrencinin kümülatif t dağılımının grafiği

Öğrenci t dağılımının özellikleri

Öğrenci t dağılımının en önemli özellikleri aşağıda gösterilmiştir.

  • Öğrenci t dağılımının alanı gerçek sayılardan oluşur.

x\in (-\infty, +\infty)

  • Birden fazla serbestlik derecesine sahip Öğrenci t dağılımları için dağılımın ortalaması 0’a eşittir.

\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Öğrenci t dağılımının varyansı aşağıdaki ifade kullanılarak hesaplanabilir:</li> </ul> <p class=\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Serbestlik derecesine bakılmaksızın Öğrenci t dağılımının medyanı ve modu her zaman 0’dır.</li> </ul> <p class=\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}

  • Öğrenci t dağılımının yoğunluk fonksiyonu aşağıdaki formülle tanımlanır:

\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}

  • Öğrenci t dağılımının kümülatif olasılık dağılım fonksiyonu aşağıdaki formülle tanımlanır:

\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}

  • Serbestlik derecesi 3’ten büyük olan Öğrenci t dağılımları için asimetri katsayısı sıfırdır çünkü bu dağılım simetriktir.

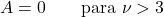
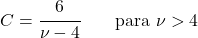\displaystyle A=0\qquad \text{para }\nu>3″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”164″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Öğrenci t dağılımının serbestlik derecesi dörtten büyükse basıklık, altının serbestlik derecesi eksi dört’e bölünmesiyle hesaplanabilir. </li> </ul> <p class=\displaystyle C=\cfrac{6}{\nu-4}\qquad \text{para }\nu>4″ title=”Rendered by QuickLaTeX.com” height=”38″ width=”198″ style=”vertical-align: -12px;”></p> </p> <h2 class= Öğrenci t dağılımının uygulamaları

Öğrenci t dağılımı istatistikte yaygın olarak kullanılan bir olasılık dağılımıdır. Aslında hipotezleri ve güven aralıklarını test etmek için kullanılan Öğrenci t testi bile vardır.

Böylece, Öğrenci t dağılımı iki örneğin ortalamaları arasındaki farkı analiz etmemizi sağlar; daha doğrusu, iki örneğin anlamlı derecede farklı ortalamalara sahip olup olmadığını belirlemek için kullanılır. Benzer şekilde, doğrusal regresyon analizinden elde edilen doğrunun eğimi olup olmadığının belirlenmesinde de Öğrenci t testi kullanılır.

Kısacası, Öğrenci t dağılımının uygulamaları teorik olarak normal bir dağılım izleyen veri setlerinin analizine dayanır ancak toplam gözlem sayısı bu tür bir dağılımı kullanmak için çok küçüktür.

yazar hakkında

Dr.Benjamin Anderson
Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yorum ekle

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir