Öğrenci t testi

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede, Öğrenci t testinin ne olduğu ve istatistikte ne için kullanıldığı açıklanmaktadır. Böylece, Öğrenci t testinin nasıl yapıldığını, farklı Öğrenci t testi türlerinin neler olduğunu ve her birinin formülünü keşfedeceksiniz.

Öğrenci t testi nedir?

Aynı zamanda T testi veya basitçe t testi olarak da adlandırılan Öğrenci t testi , test istatistiğinin Öğrencinin t dağılımını takip ettiği istatistiksel bir testtir. Bu nedenle istatistikte, Öğrenci t testi bir hipotez testinin sıfır hipotezini reddetmek veya kabul etmek için kullanılır.

Spesifik olarak, Öğrenci t testi, incelenen popülasyonun normal bir dağılım izlediği ancak örneklem boyutunun popülasyon varyansını bilmek için çok küçük olduğu hipotez testlerinde kullanılır.

Kısacası, Öğrenci t testi belirli hipotez testlerinin çalışma hipotezini reddetmek veya kabul etmek için kullanılır. Örneğin, Öğrenci t testi bir örnek, bağımsız örnekler veya ilgili örnekler için hipotezleri test etmek için kullanılır. Daha sonra her durumda Öğrenci t testinin nasıl hesaplandığını göreceğiz.

Öğrenci t-testi türleri

Üç tür Öğrenci t testi vardır:

Tek örnekli Öğrenci t testi – örnek ortalamanın değeri hakkındaki hipotezi test etmek için kullanılır.
İki bağımsız örnek için Öğrenci t testi : iki bağımsız örneğin ortalamaları arasındaki farka ilişkin hipotezi test etmenize olanak tanır.
İki eşleştirilmiş örnek (veya ilgili örnek) için Öğrenci t testi – iki kez test edilen bir örneğin ortalaması hakkındaki hipotezi araştırmak için kullanılır.

Öğrenci t testi örneği

Örnek ortalamaya yönelik hipotez testleri, testin sıfır hipotezinin ve alternatif hipotezinin popülasyon ortalamasının değeri hakkında bir şeyler söylediği testlerdir.

Tek örnekli Öğrenci t testinin formülü aşağıdaki gibidir:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Altın:

$t$

Öğrenci t dağılımı ile tanımlanan ortalamaya ilişkin hipotez testi istatistiğidir.
$\overline{x}$

örnek anlamına gelir.
$\mu$

hipotez testinde önerilen ortalamanın değeridir.
$s$

örnek standart sapmasıdır.
$n$

örneklem büyüklüğüdür.

Öğrenci t testinin değeri hesaplandıktan sonra, kritik değere sahip istatistiksel testin sonucu, sıfır hipotezinin reddedilip reddedilmeyeceği şeklinde yorumlanmalıdır:

Ortalama için hipotez testi iki taraflı ise, Öğrenci t testinin mutlak değeri _tα/2|n-1 kritik değerinden büyükse sıfır hipotezi reddedilir.
Ortalama için hipotez testi sağ kuyrukla eşleşiyorsa, Öğrencinin t-testi değeri tα _|n-1 kritik değerinden büyükse sıfır hipotezi reddedilir.
Ortalama için hipotez testi sol kuyrukla eşleşiyorsa, Öğrencinin t-testi değeri -t _α|n-1 kritik değerinden küçükse sıfır hipotezi reddedilir.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Kritik test değerlerinin Öğrenci dağılım tablosundan elde edildiğini unutmayın.

➤ Bakınız: Ortalama için hipotez testinin somut örneği

Bağımsız örnekler için student’s t testi

Bağımsız örnekler için Öğrenci t testi, iki popülasyonun ortalamaları arasındaki bir ilişkinin hipotezini reddetmek veya kabul etmek için kullanılır; örneğin, iki popülasyonun ortalamaları farklıdır veya A popülasyonunun ortalaması, ortalamadan daha büyüktür. . nüfus B.

Ancak bu durumda Öğrenci t-testi formülü popülasyon varyanslarının eşit olup olmadığına bağlı olarak değişir. Daha sonra iki olası durumu göreceğiz.

Bilinmeyen ve eşit sapmalar

Popülasyon varyanslarının bilinmediği ancak eşit olduğu varsayıldığında bağımsız örnekler için Öğrenci t testinin hesaplanmasına yönelik formül aşağıdaki gibidir:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Altın:

$t$

n ₁ + n ₂ -2 serbestlik derecesine sahip bir Öğrenci t dağılımını takip eden, bilinmeyen varyanslara sahip ortalamaların farkına yönelik hipotez test istatistiğidir.
$\mu_1$

nüfus 1’in ortalamasıdır.
$\mu_2$

nüfus 2’nin ortalamasıdır.
$\overline{x_1}$

örnek 1’in ortalamasıdır.
$\overline{x_2}$

örnek 2’nin ortalamasıdır.
$s_p$

birleştirilmiş standart sapmadır.
$n_1$

örneklem büyüklüğü 1’dir.
$n_2$

örneklem büyüklüğü 2’dir.

İki numunenin birleşik standart sapması aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Bilinmeyen ve farklı varyasyonlar

Popülasyon varyansları bilinmediğinde ve ayrıca farklı olduğu varsayıldığında, bağımsız örnekler için Öğrenci t testinin hesaplanmasına yönelik formül aşağıdaki gibidir:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Altın:

$t$

Öğrenci t dağılımını takip eden, bilinmeyen varyanslara sahip ortalamaların farkına yönelik hipotez test istatistiğidir.
$\mu_1$

nüfus 1’in ortalamasıdır.
$\mu_2$

nüfus 2’nin ortalamasıdır.
$\overline{x_1}$

örnek 1’in ortalamasıdır.
$\overline{x_2}$

örnek 2’nin ortalamasıdır.
$\sigma_1$

popülasyon 1’in standart sapmasıdır.
$\sigma_2$

popülasyon 2’nin standart sapmasıdır.
$n_1$

örneklem büyüklüğü 1’dir.
$n_2$

örneklem büyüklüğü 2’dir.

Ancak bu durumda Öğrenci t dağılımının serbestlik dereceleri aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Bakınız: Ortalamalar arasındaki farka yönelik hipotez testinin somut örneği

Eşleştirilmiş veya ilgili örnekler için Öğrenci t testi

Bu test, üzerinde çalışılan iki numune birbiriyle ilişkili olduğunda kullanılır; dolayısıyla bu, aslında iki kez (her seferinde farklı koşullar altında) analiz edilen tek bir birey numunesidir.

Örneğin, bir matematik ve istatistik dersindeki öğrenci notlarını analiz ederek iki dersin ortalamaları arasında anlamlı bir fark olup olmadığını görebilirsiniz. Bu durumda her öğrencinin matematik notu aynı öğrencinin istatistik notuna bağlanır.

Eşleştirilmiş veya ilgili örnekler için Öğrenci t-testi formülü şöyledir:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

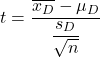
Altın:

$t$

Öğrenci t dağılımı ile tanımlanan eşleştirilmiş ortalamalar için hipotez test istatistiğidir.
$\overline{x_D}$

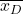
veriler arasındaki farkın oluşturduğu örneklemin ortalamasıdır.
$\mu_D$

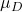
hipotez testinde önerilen ortalamanın değeridir.
$s_D$

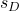
verilerdeki farkın oluşturduğu numunenin standart sapmasıdır.
$n$

örneklem büyüklüğüdür.

Öğrencinin t-testi varsayımları

Öğrenci t testini gerçekleştirmek için aşağıdaki koşulların karşılanması gerekir:

Süreklilik – Örnek veriler süreklidir.
Rastgelelik : Veri örnekleri rastgele seçilmiştir.
Homojenlik : Veri örneğinin varyansı homojendir.
Normallik – Veri örneğini tanımlayan dağılım yaklaşık olarak normaldir.

Öğrenci t testi nasıl yapılır

Son olarak, özet olarak, Öğrenci t testini gerçekleştirmek için izlenecek adımlar ayrıntılı olarak açıklanmıştır.

Hipotez testinin boş ve alternatif hipotezlerini tanımlayın.
Hipotez testinin anlamlılık düzeyini (α) belirleyin.
Öğrenci t testinin varsayımlarının karşılandığını doğrulayın.
İlgili Öğrenci t-testi formülünü uygulayın ve test istatistiğini hesaplayın.
Öğrenci t testinin sonucunu testin kritik değeriyle karşılaştırarak yorumlayın.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Öğrenci t testi nedir?

Öğrenci t-testi türleri

Öğrenci t testi örneği

Bağımsız örnekler için student’s t testi

Bilinmeyen ve eşit sapmalar

Bilinmeyen ve farklı varyasyonlar

Eşleştirilmiş veya ilgili örnekler için Öğrenci t testi

Öğrencinin t-testi varsayımları

Öğrenci t testi nasıl yapılır

yazar hakkında

Dr.benjamin anderson

Yorum ekle