Olasılık dağılımının varyansı nasıl hesaplanır

Olasılık dağılımı bize bir rastgele değişkenin belirli değerleri alma olasılığını anlatır.

Örneğin, aşağıdaki olasılık dağılımı bize belirli bir futbol takımının belirli bir maçta belirli sayıda gol atma olasılığını söyler:

Bir olasılık dağılımının varyansını bulmak için aşağıdaki formülü kullanabiliriz:

σ ² = Σ(x _ben -μ) ² * P(x _ben )

Altın:

• x _i : ^i’inci değer
• μ: Dağılımın ortalaması
• P(x _i ): ^i’inci değerin olasılığı

Örneğin futbol takımı için olasılık dağılımımızı düşünün:

Futbol takımının ortalama gol sayısı şu şekilde hesaplanacaktır:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 gol.

Daha sonra varyansı şu şekilde hesaplayabiliriz:

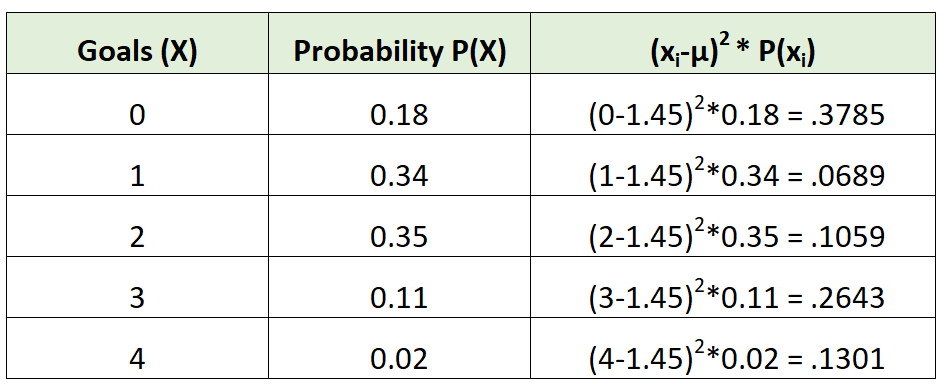
Varyans basitçe üçüncü sütundaki değerlerin toplamıdır. Yani bunu şu şekilde hesaplayacağız:

^σ2 = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475

Aşağıdaki örnekler, bir olasılık dağılımının varyansının diğer birkaç senaryoda nasıl hesaplanacağını göstermektedir.

Örnek 1: Araç arızalarındaki değişim

Aşağıdaki olasılık dağılımı bize belirli bir aracın 10 yıllık bir süre boyunca belirli sayıda akü arızası yaşama olasılığını gösterir:

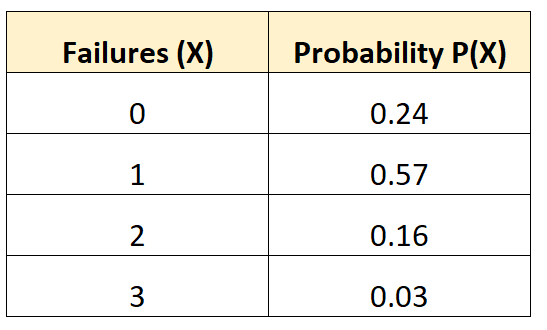
Bu olasılık dağılımının varyansını bulmak için öncelikle beklenen hataların ortalama sayısını hesaplamamız gerekir:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 başarısızlık.

Daha sonra varyansı şu şekilde hesaplayabiliriz:

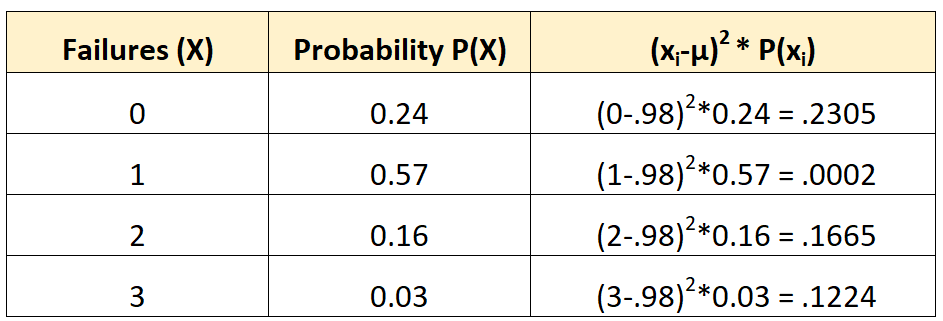
Varyans üçüncü sütundaki değerlerin toplamıdır. Yani bunu şu şekilde hesaplayacağız:

^σ2 = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196

Örnek 2: Satış varyasyonu

Aşağıdaki olasılık dağılımı bize belirli bir satıcının gelecek ay belirli sayıda satış yapma olasılığını gösterir:

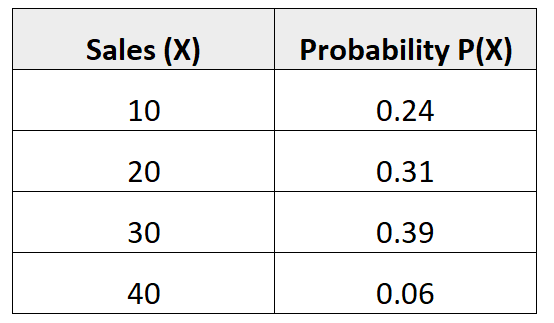
Bu olasılık dağılımının varyansını bulmak için öncelikle beklenen satışların ortalama sayısını hesaplamamız gerekir:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 kirli.

Daha sonra varyansı şu şekilde hesaplayabiliriz:

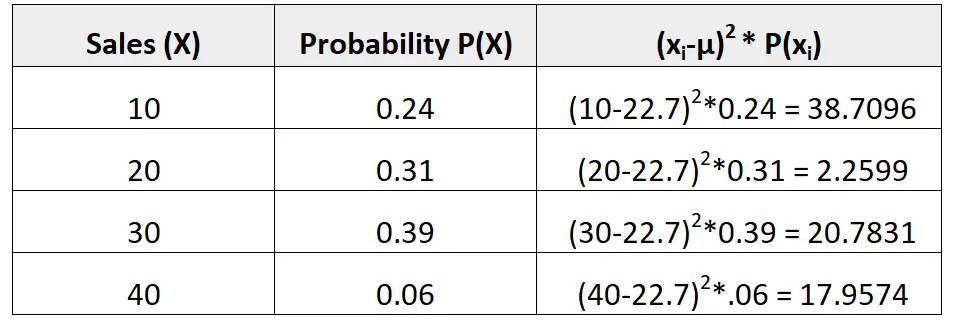
Varyans üçüncü sütundaki değerlerin toplamıdır. Yani bunu şu şekilde hesaplayacağız:

^σ2 = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71

Bu dağılımın varyansını otomatik olarak hesaplamak için olasılık dağılım hesaplayıcısını da kullanabileceğimizi unutmayın:

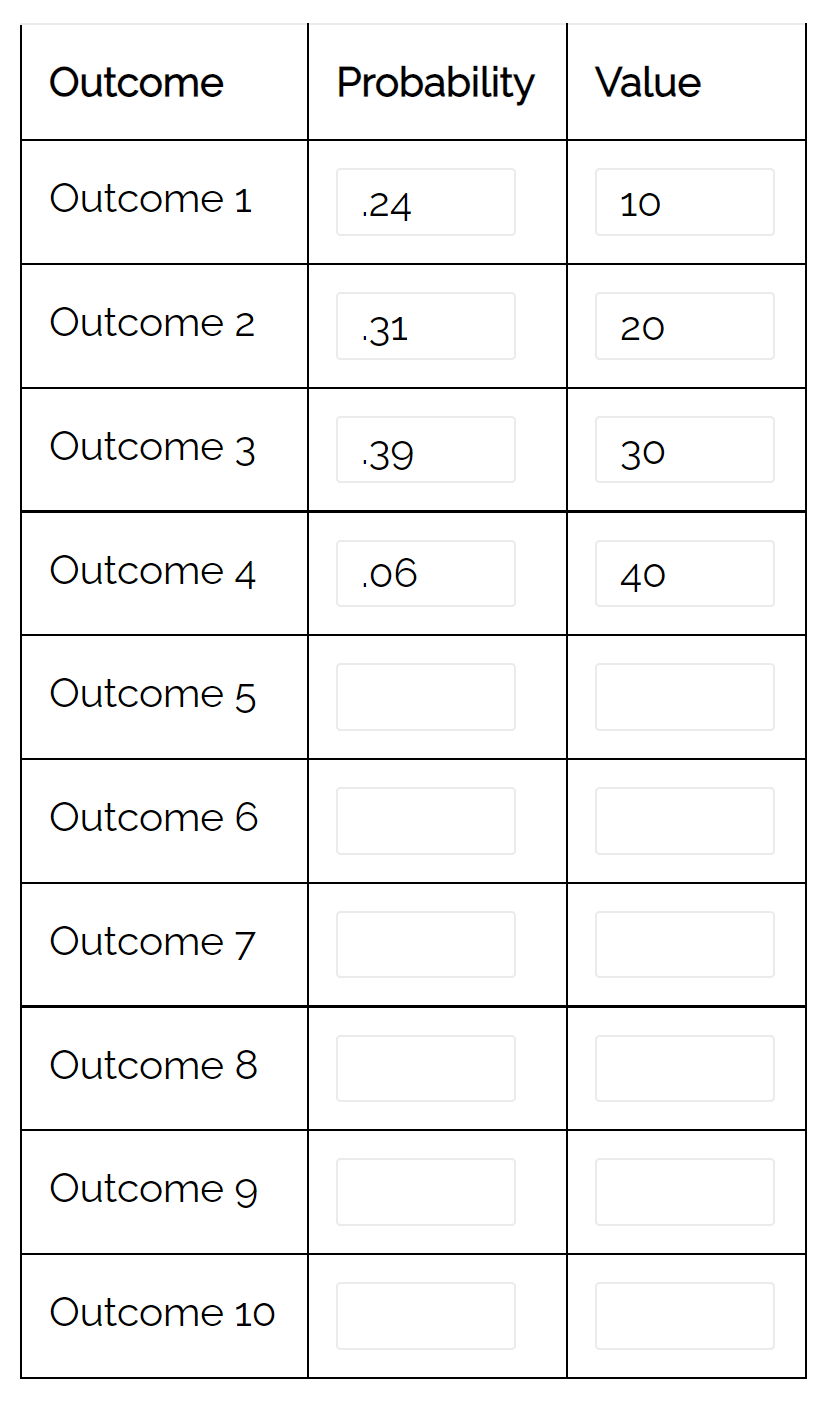
Fark 79,71 . Bu bizim manuel olarak hesapladığımız değere karşılık geliyor.