Olasılık fonksiyonu

Bu makalede olasılık fonksiyonlarının ne olduğu açıklanmaktadır. Böylece olasılık fonksiyonunun anlamını, özelliklerini ve olasılık fonksiyonunu hesaplamanın somut bir örneğini bulacaksınız. Ek olarak, bir olasılık fonksiyonu ile diğer olasılıksal fonksiyon türleri arasındaki farklar sunulmaktadır.

Olasılık fonksiyonu nedir?

Olasılık kütle fonksiyonu olarak da adlandırılan olasılık fonksiyonu, ayrı bir rastgele değişkenin belirli bir değeri alma olasılığını tanımlayan matematiksel bir fonksiyondur.

Yani bir olasılık fonksiyonu, ayrık bir değişkenin bir değere tam olarak eşit olma olasılığını döndürür.

Örneğin, bir zar atıldığında herhangi bir sayının gelme olasılığı 1/6’dır (bir zarın altı kenarı vardır), dolayısıyla bu örnek uzayla ilişkili olasılık fonksiyonu, hangi değer olursa olsun n için 1/6’ya eşit olacaktır.

Olasılık fonksiyonunun özellikleri

Olasılık fonksiyonları aşağıdaki özelliklere sahiptir:

• Olasılıklar negatif olamaz, dolayısıyla olasılık fonksiyonu herhangi bir x değeri için sıfır veya pozitiftir.

• Aynı şekilde maksimum olasılık birliktir, yani olay her zaman meydana gelecektir. Bu nedenle olasılık fonksiyonunun maksimum değeri 1’e eşittir.

• Son olarak, bir olasılık fonksiyonunun tüm değerlerinin toplamı, örnek uzaydaki tüm olasılıkların toplamı olduğundan 1 verir.

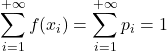
Olasılık Fonksiyonu Örneği

Artık olasılık fonksiyonunun tanımını ve özelliklerini bildiğimize göre, bu tür olasılık fonksiyonunun bir örneğini görelim.

• Dört bağımsız yazı-tura atışı yaparak 0, 1, 2, 3 ve 4 kez tura gelme olasılığını hesaplayın. Daha sonra bulunan olasılık fonksiyonunun grafiğini çizin.

Öncelikle tura gelme olasılıklarını hesaplamalıyız, bunun için olası vakaları toplam vaka sayısına bölmeliyiz. Tüm olasılıkların hesaplamasını aşağıdaki tabloda görebilirsiniz:

Ve tüm olasılıkları hesapladıktan sonra olasılık fonksiyonunun değerlerini bir grafik üzerinde gösterebiliriz:

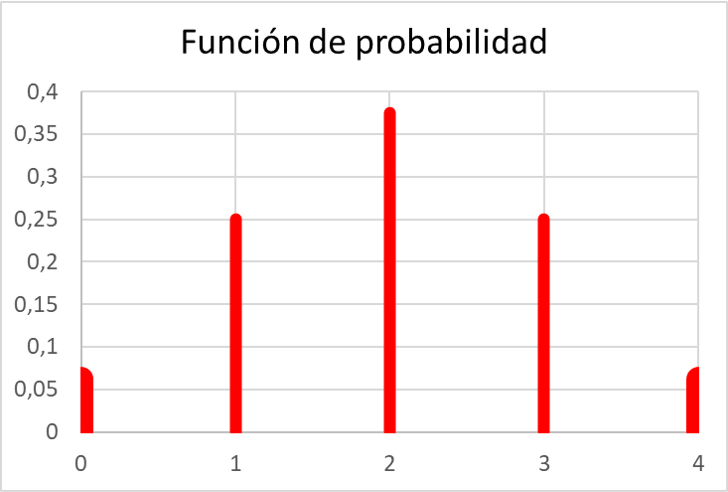
Gördüğünüz gibi alıştırmadaki olasılık fonksiyonu, tüm değerleri 0 ile 1 arasında olduğundan ve üstelik tüm değerlerinin toplamı 1’e eşit olduğundan olasılık fonksiyonlarının tüm özelliklerini karşılamaktadır.

Olasılık fonksiyonu ve yoğunluk fonksiyonu

Bu bölümde olasılık fonksiyonu ile yoğunluk fonksiyonu arasındaki farkı göreceğiz çünkü bunlar aynı amaca sahip ancak farklı durumlarda kullanılan iki tür olasılık fonksiyonudur.

Olasılık fonksiyonu ile yoğunluk fonksiyonu arasındaki fark, olasılıkların tanımladığı değişken türüdür. Olasılık fonksiyonu ayrık bir değişkenin olasılıklarını tanımlamak için kullanılırken, yoğunluk fonksiyonu sürekli bir değişkenin olasılıklarını tanımlamak için kullanılır.

Dolayısıyla değişkene bağlı olarak bir olasılık fonksiyonu veya yoğunluk fonksiyonu kullanılır.

Yoğunluk işlevi hakkında daha fazla bilgi edinmek için aşağıdaki bağlantıya tıklayın:

Olasılık fonksiyonu ve dağılım fonksiyonu

Bir olasılık fonksiyonu ile bir dağılım fonksiyonu arasındaki fark, tanımladıkları olasılık türüdür. Olasılık fonksiyonu değişkenin belirli bir değer alma olasılığını belirtirken, dağılım fonksiyonu değişkenin kümülatif olasılığını açıklar.

Bu nedenle dağılım fonksiyonu olasılık fonksiyonundan hesaplanır.

Örnek olarak aşağıdaki bağlantıda, yukarıdaki alıştırmada bulunan olasılık fonksiyonuna dayalı olarak, dört yazı-tura atıldığında tura gelmesine yönelik dağıtım fonksiyonunun hesaplanmasını görebilirsiniz.