Olayların kesişme olasılığı

Bu makalede olayların kesişme olasılığının nasıl hesaplanacağı açıklanmaktadır. Böylece olayların kesişme olasılığının formülünün ne olduğunu ve ayrıca adım adım çözülen alıştırmaları öğreneceksiniz.

Olayların kesişimi nedir?

Olasılık teorisinde olayların kesişmesi , sonucu operasyonun tüm olaylarında ortak olan temel olaylardan oluşan olayların bir operasyonudur. Yani A ve B olaylarının kesişimi, aynı anda A ve B’ye ait olan tüm olayların birleşiminden oluşur.

İki olayın kesişimi ⋂ sembolü ile ifade edilir. Böylece A ve B olaylarının kesişimi A⋂B olarak yazılır.

Örneğin, bir zarın rastgele atılması deneyinde, eğer bir olay bir çift sayının A={2, 4, 6} atılmasıysa ve başka bir olay da üçten büyük bir sayının B={4, 5 atılmasıysa, 6 } ise iki olayın kesişimi A⋂B={4, 6}’tır.

Olayların kesişme olasılığı formülü

İki olayın kesişme olasılığı, bir olayın meydana gelme olasılığı ile ilk olay göz önüne alındığında diğer olayın koşullu olasılığının çarpımına eşittir.

Bu nedenle, iki olayın kesişme olasılığı formülü P(A⋂B)=P(A) P(B|A)=P(B) P(A|B) şeklindedir.

Altın:

• 

  Ve

  

  Bunlar iki bağımlı olaydır.

• 

  A olayı ile B olayının kesişme olasılığıdır.

• 

  A olayının gerçekleşme olasılığıdır.

• 

  A olayı verildiğinde B olayının meydana gelme koşullu olasılığıdır.

• 

  B olayının gerçekleşme olasılığıdır.

• 

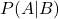
  verilen B olayının meydana gelmesinin koşullu olasılığıdır.

Ancak iki olay bağımsızsa bu, bir olayın meydana gelme olasılığının diğer olayın meydana gelip gelmemesine bağlı olmadığı anlamına gelir. Bu nedenle iki bağımsız olayın kesişme olasılığı formülü aşağıdaki gibidir:

Altın:

• 

  Ve

  

  Bunlar iki bağımsız olaydır.

• 

  A olayı ile B olayının kesişme olasılığıdır.

• 

  A olayının gerçekleşme olasılığıdır.

• 

  B olayının gerçekleşme olasılığıdır.

Olay kesişme olasılığına ilişkin gerçek dünyadan örnekler

Daha sonra size adım adım çözülmüş iki örnek bırakıyoruz, böylece iki olayın kesişme olasılığının nasıl hesaplandığını görebilirsiniz. Önce iki bağımsız olayın, sonra da iki bağımlı olayın kesişimine ilişkin bir örnek göreceğiz, böylece her iki durumu da görebilirsiniz.

İki bağımsız olayın kesişme olasılığı

• Art arda üç kez çekiliş başlatılır. Her üç atışta da tura gelme olasılığını bulun.

Bu durumda ortak olasılığını hesaplamak istediğimiz olaylar bağımsızdır çünkü bir çekilişin sonucu bir önceki çekilişte elde edilen sonuca bağlı değildir. Bu nedenle, ardı ardına üç tura gelme olasılığını belirlemek için bağımsız olaylara ilişkin kesişim olasılığı formülünü kullanmalıyız:

Kura çekerken yalnızca iki olası sonuç vardır; tura veya yazı gelebilir. Buna göre, bir para atıldığında yazı veya tura gelme olasılığı:

Dolayısıyla, üç yazı tura atışında da tura gelme olasılığını bulmak için, tura gelme olasılığını üçle çarpmamız gerekir:

Kısacası art arda üç kez tura gelme olasılığı %12,5’tir.

İki bağımlı olayın kesişme olasılığı

• Boş bir kutuya 8 mavi top, 4 turuncu top ve 2 yeşil top koyuyoruz. İlk çekilen topu kutuya geri koymadan önce bir top, sonra başka bir top çekersek, ilk topun mavi, ikinci topun turuncu olma olasılığı nedir?

Bu durumda olaylar bağımlıdır çünkü ikinci çekilişte turuncu bir top alma olasılığı, ilk çekilişte çekilen topun rengine bağlıdır. Bu nedenle, problemin bize sorduğu olasılığı hesaplamak için bağımlı olayların kesişme olasılığı formülünü kullanmalıyız:

İlk çekilişte mavi top alma olasılığını belirlemek kolaydır; mavi topların sayısını toplam top sayısına bölmeniz yeterlidir:

Öte yandan, mavi bir top aldıktan sonra turuncu bir top çekme olasılığı, turuncu topların sayısı farklı olduğundan ve ayrıca kutunun içinde artık bir top eksildiğinden farklı şekilde hesaplanır:

Böylece önce mavi, sonra turuncu top çekme olasılığı yukarıda bulunan iki olasılığın çarpılmasıyla hesaplanır:

Olay Kavşak Özellikleri

Olasılık teorisinde olayların kesişimi aşağıdaki özelliklere sahiptir:

• Değişme özelliği: Kesişme olaylarının sırası işlemin sonucunu değiştirmez.

• İlişkisel özellik: Sonuç aynı olduğundan, üç olayın kesişimi herhangi bir sırayla hesaplanabilir.

• Dağıtıcı özellik: Olayların kesişimi, olayların birleşimindeki dağıtıcı özelliği karşılar.