Python'da ols regresyon nasıl gerçekleştirilir (örnekle)

Sıradan en küçük kareler (OLS) regresyonu, bir veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi en iyi tanımlayan doğruyu bulmamızı sağlayan bir yöntemdir.

Bu yöntem aşağıdaki denklemi bulmamızı sağlar:

ŷ = b ₀ + b ₁ x

Altın:

• ŷ : Tahmini yanıt değeri
• b ₀ : Regresyon çizgisinin başlangıcı
• b ₁ : Regresyon çizgisinin eğimi

Bu denklem, yordayıcı ile yanıt değişkeni arasındaki ilişkiyi anlamamıza yardımcı olabilir ve yordayıcı değişkenin değeri göz önüne alındığında bir yanıt değişkeninin değerini tahmin etmek için kullanılabilir.

Aşağıdaki adım adım örnek, Python’da OLS regresyonunun nasıl gerçekleştirileceğini gösterir.

1. Adım: Verileri oluşturun

Bu örnekte 15 öğrenci için aşağıdaki iki değişkeni içeren bir veri seti oluşturacağız:

• Toplam çalışılan saat sayısı
• Sınav sonucu

Tahmin edici değişken olarak saatleri ve yanıt değişkeni olarak sınav puanını kullanarak bir OLS regresyonu gerçekleştireceğiz.

Aşağıdaki kod, bu sahte veri kümesinin pandalarda nasıl oluşturulacağını gösterir:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

2. Adım: Bir OLS regresyonu gerçekleştirin

Daha sonra, tahmin değişkeni olarak saatleri ve yanıt değişkeni olarak puanı kullanarak bir OLS regresyonu gerçekleştirmek için statsmodels modülündeki işlevleri kullanabiliriz:

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Katsayı sütunundan regresyon katsayılarını görebilir ve aşağıdaki uygun regresyon denklemini yazabiliriz:

Puan = 65,334 + 1,9824*(saat)

Bu, çalışılan her ek saatin ortalama 1,9824 puanlık sınav puanı artışıyla ilişkili olduğu anlamına gelir.

Orijinal değeri olan 65.334 bize sıfır saat ders çalışan bir öğrencinin ortalama beklenen sınav puanını anlatır.

Bu denklemi, öğrencinin ders çalıştığı saat sayısına göre beklenen sınav puanını bulmak için de kullanabiliriz.

Örneğin 10 saat ders çalışan bir öğrencinin sınav puanının 85.158 olması gerekir:

Puan = 65,334 + 1,9824*(10) = 85,158

Model özetinin geri kalanını şu şekilde yorumlayabilirsiniz:

• P(>|t|): Model katsayılarıyla ilişkili p değeridir. Saatlere ilişkin p değeri (0,000) 0,05’ten küçük olduğundan saat ile puan arasında istatistiksel olarak anlamlı bir ilişkinin olduğunu söyleyebiliriz.
• R-kare: Bu bize sınav puanlarındaki değişim yüzdesinin çalışılan saat sayısıyla açıklanabileceğini söyler. Bu durumda puanlardaki değişimin %83,1’i çalışılan saatlerle açıklanabilir.
• F istatistiği ve p değeri: F istatistiği ( 63.91 ) ve karşılık gelen p değeri ( 2.25e-06 ) bize regresyon modelinin genel önemini, yani modeldeki yordayıcı değişkenlerin varyasyonu açıklamada yararlı olup olmadığını anlatır. yanıt değişkeninde. Bu örnekteki p değeri 0,05’ten küçük olduğundan modelimiz istatistiksel olarak anlamlıdır ve saatlerin puan değişimini açıklamada faydalı olduğu düşünülmektedir.

3. Adım: En uygun çizgiyi görselleştirin

Son olarak, gerçek veri noktalarına uygun regresyon çizgisini görselleştirmek için matplotlib veri görselleştirme paketini kullanabiliriz:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

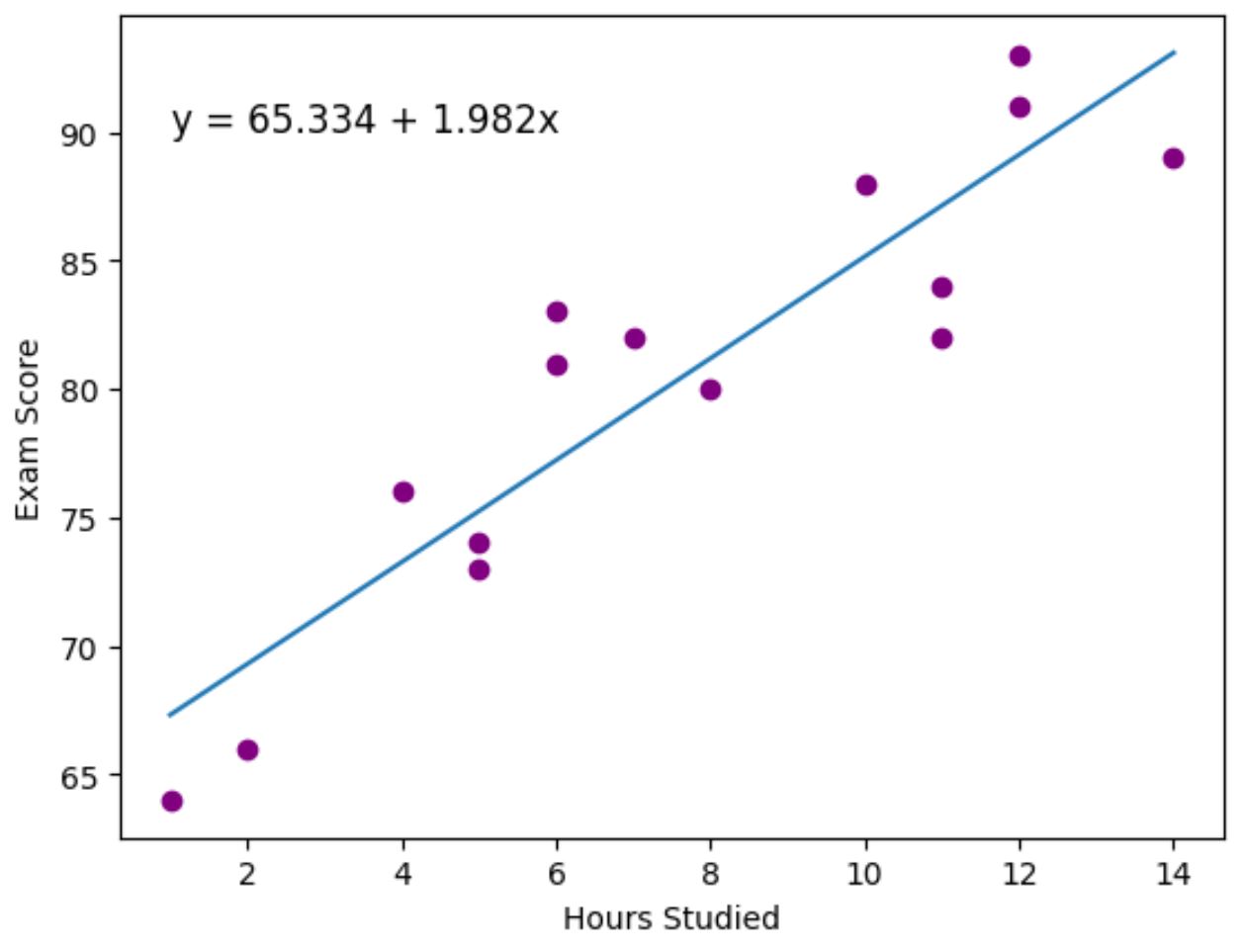
Mor noktalar gerçek veri noktalarını temsil eder ve mavi çizgi ise takılan regresyon çizgisini temsil eder.

Ayrıca uygun regresyon denklemini grafiğin sol üst köşesine eklemek için plt.text() fonksiyonunu kullandık.

Grafiğe bakıldığında, uygun regresyon çizgisinin saat değişkeni ile puan değişkeni arasındaki ilişkiyi oldukça iyi yakaladığı görülmektedir.

Ek kaynaklar

Aşağıdaki eğitimlerde Python’da diğer genel görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Python’da Lojistik Regresyon Nasıl Gerçekleştirilir
Python’da Üstel Regresyon Nasıl Gerçekleştirilir
Python’da regresyon modellerinin AIC’si nasıl hesaplanır