Ondalık
Bu yazıda ondalık sayıların ne olduğunu ve nasıl hesaplandıklarını açıklıyoruz. Ayrıca, ondalık hesaplamaların birkaç adım adım çözülmüş örneğini bulacaksınız ve buna ek olarak, çevrimiçi bir hesap makinesiyle herhangi bir istatistiksel örneğin ondalıklarını hesaplayabileceksiniz.
Ondalık dilimler nedir?
İstatistikte ondalık sayılar, sıralı bir veri kümesini on eşit parçaya bölen dokuz değerdir. Böylece birinci, ikinci, üçüncü,… ondalık dilim numunenin veya popülasyonun %10, %20, %30,…’unu temsil eder.
Örneğin dördüncü ondalık değer, verinin %40’ından yüksek, ancak geri kalan veriden düşüktür.
Ondalık dilimler büyük D harfi ve ondalık indeks ile temsil edilir, yani ilk ondalık dilim D 1 , ikinci ondalık dilim D 2 , üçüncü ondalık dilim D 3 vb.
👉Herhangi bir veri kümesi için ondalık değerleri hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.
Ondalık dilimlerin, çeyrekler, beşte birlik dilimler ve yüzdelik dilimlerle aynı şekilde merkezi olmayan konumun bir ölçüsü olduğuna dikkat edilmelidir. Bu nicelik türlerinin her birinin anlamını web sitemizden kontrol edebilirsiniz.
Ayrıca beşinci ondalık dilim, tüm veri setini iki eşit parçaya böldüğü için medyan ve ikinci çeyreğe eşdeğerdir.
Ondalık sayı nasıl hesaplanır
Bir dizi istatistiksel verinin ondalık konumunu hesaplamak için, ondalık sayıyı toplam veri sayısının toplamının bir artısıyla çarpın ve sonucu ona bölün.
Bu nedenle ondalık formül şu şekildedir:
![]()
Lütfen unutmayın: Bu formül bize ondalık dilimin değerini değil, ondalık dilimin konumunu söyler. Ondalık kısım, formül tarafından elde edilen konumda bulunan veriler olacaktır.
Ancak bazen bu formülün sonucu bize ondalık sayı verir, bu nedenle sonucun ondalık sayı olup olmadığına bağlı olarak iki durumu ayırmamız gerekir:
- Formülün sonucu ondalık kısmı olmayan bir sayı ise, ondalık kısım yukarıdaki formülün sağladığı konumda bulunan verilerdir.
- Formülün sonucu ondalık kısmı olan bir sayı ise, ondalık değer aşağıdaki formül kullanılarak hesaplanır:
![]()
Burada x i ve x i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.
Şimdi istatistiksel bir örneğin ondalık rakamlarını almanın karmaşık olduğunu düşünebilirsiniz, ancak pratikte oldukça basittir. Aşağıdaki iki örneği okursanız mutlaka çok daha iyi anlayacaksınız.
Not : Bilim camiası ondalık sayıların nasıl hesaplanacağı konusunda tam olarak fikir birliğine varmamıştır, dolayısıyla bunu biraz farklı açıklayan istatistik kitaplarını bulabilirsiniz.
Ondalık hesaplama örneği
Yukarıda gördüğünüz gibi ondalık sayıların hesaplanması, ilk formülün bize verdiği sayının ondalık olup olmamasına bağlıdır, bu yüzden aşağıda her durum için bir tane olmak üzere iki çözümlü örnek hazırladık. Her durumda, ondalık dilimlerin bileşimi hakkında herhangi bir sorunuz varsa, bunları yorumlarda sorabileceğinizi unutmayın.
örnek 1
- Aşağıdaki veriler göz önüne alındığında, en küçükten en büyüğe, numunenin birinci, üçüncü ve sekizinci dilimini bulun.

Bu alıştırmadaki veriler zaten sıralanmıştır, bu nedenle sırayı değiştirmeye gerek yoktur, aksi takdirde önce verileri en küçükten en büyüğe doğru sıralamak zorunda kalırız.
Yukarıda açıklandığı gibi ondalık sayıların konumlarını bulmayı mümkün kılan formül aşağıdaki gibidir:
![]()
Bu alıştırmanın örneklem büyüklüğü 29 gözlemdir, dolayısıyla ilk ondalık dilimin konumunu hesaplamak için n yerine 29 ve k yerine 1 koymalısınız:
![]()
Formülün sonucu 3 olduğundan ilk ondalık dilim sıralı listenin üçüncü konumunda olacaktır ve bu değer 85’e karşılık gelir.
Şimdi aynı işlemi üçüncü ondalık dilimle tekrar uyguluyoruz. K’yı 3 ile değiştirerek formülü kullanırız:
![]()
Bu nedenle üçüncü ondalık dilim dokuzuncu konumdaki öğe olacaktır, yani 97.
Son olarak aynı işlemi yapıyoruz ancak sekizinci ondalık dilimi belirlemek için formüle 8 koyuyoruz:
![]()
Sekizinci ondalık dilim, sıralı veri listesinin 24. pozisyonundaki sayı olacaktır, dolayısıyla sekizinci ondalık dilim 131 olacaktır.
Örnek 2
- Aşağıdaki tablodaki verilerden 4, 7 ve 9 ondalıklarını hesaplayın.

Önceki örnekte olduğu gibi, ondalık sayıların konumlarını elde etmek için aşağıdaki formülü kullanmanız gerekir:
![]()
Bu durumda örneklem büyüklüğü 42’dir, dolayısıyla dördüncü ondalık dilimin konumunu bulmak için n parametresini 42 ve k parametresini 4 ile değiştirmeniz gerekir:
![]()
Ancak bu sefer formülden ondalık bir sayı aldık, dolayısıyla tam ondalık değeri hesaplamak için aşağıdaki formülü uygulamamız gerekiyor:
![]()
İlk formülden elde edilen sayı 17,2’dir, yani dördüncü ondalık dilim, sırasıyla 109 ve 112 olan on yedinci ve on sekizinci sayılar arasındadır. Bu nedenle x i 109, x i+ 1 112 ve d ondalık kısımdır. elde edilen sayının 0,2’si.
![]()
Yedinci ondalık dilimi bulmak için aynı işlemi tekrarlıyoruz. İlk önce ondalık dilimin konumunu hesaplıyoruz:
![]()
Formülden 30.1 sayısını elde ettik, bu da ondalık dilimin 30 ile 31 konumları arasında olacağı anlamına gelir, değerleri 154 ve 159’dur. Bu nedenle tam ondalık hesaplama şu şekildedir:
![]()
Son olarak dokuzuncu ondalık dilimi elde etmek için aynı yöntemi tekrar uyguluyoruz. Ondalığın konumunu belirliyoruz:
![]()
Elde edilen sayı ondalıktır ve 38 ile 39 arasındadır ve konumları 189 ile 196 değerlerine karşılık gelir. Dolayısıyla ondalık 9’un hesaplanması şu şekildedir:
![]()
Ondalık Hesaplayıcı
Ondalıkları hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti takın. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Gruplandırılmış verilerdeki ondalık sayılar
Veriler aralıklar halinde gruplandırıldığında ondalık dilimleri hesaplamak için öncelikle aşağıdaki formülü kullanarak ondalık dilimin düştüğü aralığı veya bölmeyi bulmamız gerekir:
![]()
Dolayısıyla ondalık dilim, mutlak frekansı önceki ifadede elde edilen sayıdan hemen büyük olan aralıkta olacaktır.
Ve ondalık dilimin ait olduğu aralığı zaten bildiğimizde, ondalık dilimin tam değerini bulmak için aşağıdaki formülü uygulamamız gerekir:
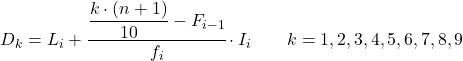
Altın:
- L i, ondalık dilimin bulunduğu aralığın alt sınırıdır.
- n , istatistiksel verilerin toplam sayısıdır.
- F i-1 önceki aralığın kümülatif mutlak frekansıdır.
- f i, ondalık dilimin bulunduğu aralığın mutlak frekansıdır.
- ben i ondalık aralığın genişliğidir.
Bunun nasıl yapıldığını görebilmeniz için aşağıda, aralıklara göre gruplandırılmış aşağıdaki verilerin 3, 5 ve 8’inci ondalıklarının hesaplandığı tamamlanmış bir alıştırmanız var.
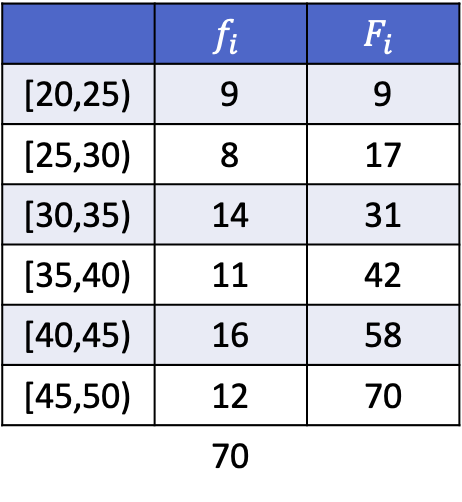
Veriler gruplandırıldığı için her ondalık dilimin hesaplanması iki adımdan oluşur: önce ondalık dilimin düştüğü aralığı bulun, ardından ondalık dilimin tam değerini hesaplayın. Bu nedenle üçüncü ondalık dilimin aralığını buluyoruz:
![]()
![]()
Ondalık aralık, mutlak kümülatif frekansı 21,3’ten hemen büyük olan aralık olacaktır ve bu durumda mutlak kümülatif frekansı 31 olan aralıktır [30,35). Artık ondalık aralığını bildiğimize göre, bulmak için aşağıdaki formülü uygularız. ondalık dilimin tam değeri:
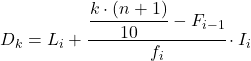
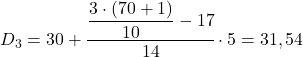
Şimdi beşinci ondalık dilimi elde etmek için yöntemi yeniden uygulamamız gerekiyor. İlk önce bulunduğu aralığı belirleriz:
![]()
Sonuç 35, [35,40) aralığında olduğu anlamına gelir, ancak aralık ifadesinde 35 olduğu için değil, birikmiş mutlak frekansının (42) en doğrudan yüksek olması nedeniyle. Aralık belirlendikten sonra sürecin ikinci formülünü uygularız:
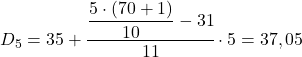
Son olarak sekizinci ondalık dilimi buluyoruz. Bunu yapmak için önce aralığını hesaplıyoruz:
![]()
56,8’in hemen üzerindeki kümülatif mutlak frekans 58’dir, yani sekizinci ondalık aralık [40,45’tir. Bu nedenle ondalık dilimin tam değerini belirlemek yeterlidir: