Ondalık sayılarla kök ve yaprak grafiği nasıl oluşturulur

Kök ve yaprak grafiği, bir veri kümesindeki her değeri bir “kök” ve “yaprak” olarak bölerek verileri görüntüleyen bir grafik türüdür.

Örneğin aşağıdaki veri setine sahip olduğumuzu varsayalım:

Veri kümesi: 12, 14, 18, 22, 22, 23, 25, 25, 28, 45, 47, 48

Her değerin ilk rakamını “gövde”, ikinci rakamını da “yaprak” olarak tanımlarsak aşağıdaki kök ve yaprak diyagramını oluşturabiliriz:

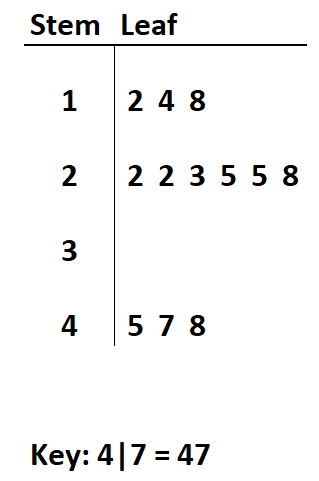
Kök ve yaprak grafikleri genellikle tamsayı değerlerle kullanılsa da ondalık basamaklı değerler için de kullanılabilir.

Aşağıdaki örnekler, ondalık sayılarla kök ve yaprak grafiklerinin nasıl oluşturulacağını göstermektedir.

Örnek 1: Tek Ondalık Basamaklı Gövde ve Yaprak Grafiği

Aşağıdaki veri setine sahip olduğumuzu varsayalım:

Veri kümesi: 11.6, 12.2, 12.5, 12.6, 13.7, 13.8, 14.1, 15.2

Virgülden önceki sayıları kök, virgülden sonraki sayıları da yaprak olarak tanımlarsak aşağıdaki kök ve yaprak diyagramını oluşturabiliriz:

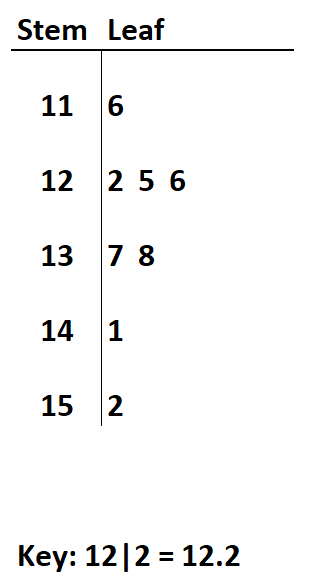
Bu gövde ve yaprak grafiğini oluştururken, okuyucunun gövde ve yaprak değerlerini nasıl yorumlayacağını bilmesi için alt tarafa bir anahtar eklemek önemlidir.

Örnek 2: Çoklu Ondalık Basamağa Sahip Gövde ve Yaprak Grafiği

Aşağıdaki veri setine sahip olduğumuzu varsayalım:

Veri kümesi: 3,26, 3,28, 3,34, 3,38, 3,41, 3,42, 3,44, 3,59, 3,63

Tam sayıyı ve virgülden sonraki ilk değeri kök, virgülden sonraki ikinci değeri ise yaprak olarak ayarlarsak, aşağıdaki kök ve yaprak grafiğini oluşturabiliriz:

Yine grafiğin alt kısmındaki anahtar bize grafik değerlerinin nasıl yorumlanacağını anlatır.

Örnek 3: Bir Kök ve Yaprak Diyagramını Ondalık Sayılarla Yorumlama

Diyelim ki ondalık sayılarla birlikte aşağıdaki kök ve yaprak diyagramına sahibiz:

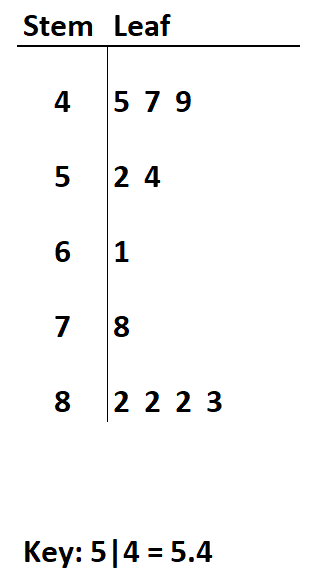
Soru 1: Veri kümesindeki maksimum değer nedir?

Maksimum değer 8,3 olacaktır.

Soru 2: Veri setinin kapsamı nedir?

Veri kümesinin aralığı en büyük ve en küçük değer arasındaki farktır. Yani aralık 8,3 – 4,5 = 3,8 olacaktır.

Soru 3: Veri kümesinin modu nedir?

Mod, en sık görünen değerdir. Bu 8.2 olurdu.

Soru 4: Veri setinin medyanı nedir?

Medyan, veri setinin “ortalama” değeri olarak tanımlanır. Bu değeri bulmak için tek tek değerlerin her birini veri setine yazıp ortanca değerini bulabiliriz:

Veri kümesi: 4.5, 4.7, 4.9, 5.2, 5.4, 6.1 , 7.8, 8.2, 8.2, 8.2, 8.3

Medyan 6,1’dir .

Ek kaynaklar

Kök ve Yaprak Grafiklerine Giriş
Sırt sırta gövde ve yaprak grafiklerine giriş
Kök ve Yaprak Grafiği Oluşturucu
Excel’de Kök ve Yaprak Grafiği Nasıl Oluşturulur