Oran oranları nasıl yorumlanır?

İstatistikte olasılık , bir olayın meydana gelme ihtimalini ifade eder. Aşağıdaki şekilde hesaplanır:

OLASILIK:

P(olay) = (# arzu edilen sonuçlar) / (# olası sonuçlar)

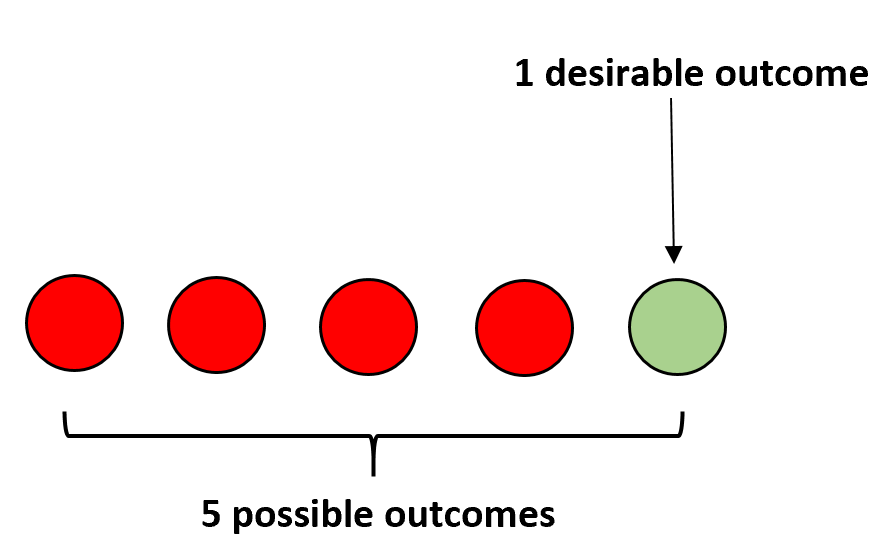
Örneğin bir torbada dört kırmızı ve bir yeşil topumuz olduğunu varsayalım. Gözlerinizi kapatıp rastgele bir top seçerseniz yeşil top seçme olasılığınız şu şekilde hesaplanır:

P(yeşil) = 1/5 = 0,2 .

Bir olayın gerçekleşme olasılığı şu şekilde hesaplanabilir:

Oranlar:

Şans (olay) = P (olay meydana gelir) / 1-P (olay meydana gelir)

Örneğin yeşil topa atış yapma ihtimali (0,2)/1-(0,2) = 0,2/0,8 = 0,25’tir .

Olasılık oranı iki olasılığın oranıdır.

ŞANS RAPORU:

Oran Oranı = A Olayının Oranı / B Olayının Oranı

Örneğin, kırmızı top ile yeşil topun seçilmesi arasındaki olasılık oranını hesaplayabiliriz.

Kırmızı topun çekilme olasılığı 4/5 = 0,8’dir .

Kırmızı top çekme şansı (0,8) / 1-(0,8) = 0,8 / 0,2 = 4’tür .

Yeşil top yerine kırmızı topun seçilmesine ilişkin olasılık oranı şu şekilde hesaplanır:

Oranlar (kırmızı) / Oranlar (yeşil) = 4 / 0,25 = 16 .

Yani kırmızı topa vurma şansı, yeşil topa vurma şansından 16 kat daha fazladır.

Gerçek dünyada olasılık oranları ne zaman kullanılır?

Gerçek dünyada olasılık oranları, araştırmacıların iki olayın meydana gelme olasılığını karşılaştırmak istediği çeşitli bağlamlarda kullanılır. İşte bazı örnekler.

Örnek #1: Olasılık oranlarının yorumlanması

Araştırmacılar, yeni bir tedavinin, mevcut tedaviye kıyasla hastanın olumlu bir sağlık sonucu yaşama şansını artırıp artırmadığını bilmek istiyor. Aşağıdaki tablo, tedaviye bağlı olarak olumlu veya olumsuz sağlık sonucu yaşayan hastaların sayısını göstermektedir.

Bir hastanın yeni tedaviden olumlu sonuç alma şansı şu şekilde hesaplanabilir:

Şans = P(pozitif) / 1 – P(pozitif) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25

Bir hastanın mevcut tedaviyle olumlu bir sonuç elde etme şansı şu şekilde hesaplanabilir:

Şans = P(pozitif) / 1 – P(pozitif) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875

Böylece yeni tedavinin mevcut tedaviye göre olumlu sonuç elde etme olasılık oranı şu şekilde hesaplanabilir:

Olasılık oranı = 1,25 / 0,875 = 1,428 .

Bunu , bir hastanın yeni tedaviyi kullanarak olumlu sonuç alma şansının, bir hastanın mevcut tedaviyi kullanarak olumlu sonuç alma şansının 1,428 katı olduğu şeklinde yorumluyoruz.

Yani yeni tedaviyle olumlu sonuç alma şansı yüzde 42,8 arttı.

Örnek #2: Olasılık oranlarının yorumlanması

Pazarlamacılar, bir reklamın müşterilerin belirli bir ürünü başka bir reklama göre daha sık satın almasını sağlayıp sağlamadığını bilmek ister. Yani her reklamı 100 kişiye gösteriyorlar. Aşağıdaki tablo, gördükleri reklama göre ürünü satın alan kişilerin sayısını göstermektedir:

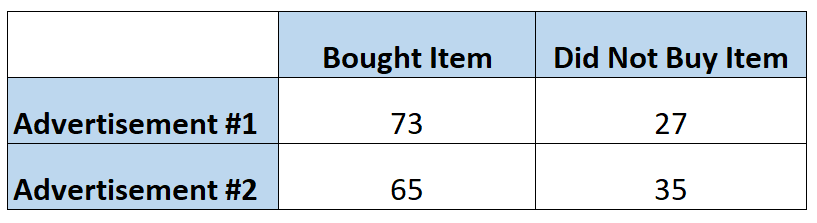
Bir kişinin ilk reklamı gördükten sonra ürünü satın alma şansı şu şekilde hesaplanabilir:

Oranlar = P(alındı) / 1 – P(alındı) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704

Bir kişinin ikinci reklamı gördükten sonra ürünü satın alma şansı şu şekilde hesaplanabilir:

Oranlar = P(alındı) / 1 – P(alındı) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857

Dolayısıyla, bir müşterinin ilk reklamı gördükten sonra ürünü satın alması ile ikinci reklamı gördükten sonra satın alması arasındaki olasılık oranı şu şekilde hesaplanabilir:

Olasılık oranı = 2,704 / 1,857 = 1,456 .

Bunu , bir kişinin ilk reklamı gördükten sonra ürünü satın alma ihtimalinin, bir kişinin ikinci reklamı gördükten sonra ürünü satın alma ihtimalinin 1,456 katı olduğu şeklinde yorumluyoruz.

Yani ilk listeleme sayesinde ürünü satın alma şansı %45,6 artıyor.

Ek kaynaklar

Excel’de Oran Oranı ve Göreli Risk Nasıl Hesaplanır?
1’den küçük bir olasılık oranı nasıl yorumlanır?
Göreceli risk nasıl yorumlanır?