Oranlardaki farkın örnekleme dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede orantısal örnekleme dağılımındaki farkın ne olduğu ve istatistikte ne için kullanıldığı açıklanmaktadır. Oranlardaki fark örnekleme dağılım formülü ve adım adım çözülmüş bir alıştırma da sunulmaktadır.

Oranlardaki farkın örneklem dağılımı nedir?

Orantısal örnekleme dağılımındaki fark , iki farklı popülasyondan olası tüm örneklerin örnekleme oranları arasındaki farkların hesaplanmasından kaynaklanan dağılımdır.

Yani, oranlardaki farkın örnekleme dağılımını elde etme süreci, ilk olarak iki farklı popülasyondan olası tüm örneklerin çıkarılması, ikinci olarak çıkarılan her örneğin oranının belirlenmesi ve son olarak tüm popülasyonlar arasındaki farkın belirlenmesidir. oranlar farkının oranları. iki popülasyon. Böylece bu işlemler yapıldıktan sonra elde edilen sonuçlar kümesi, orantısal farkın örnekleme dağılımını oluşturur.

İstatistikte, orantısal örnekleme dağılımındaki fark, rastgele seçilen iki örneğin örneklem oranları arasındaki farkın popülasyon oranlarındaki farka yakın olma olasılığını hesaplamak için kullanılır.

➤ Bakınız: Orantılı Örnekleme Tahsisi

Oran Farkının Örnekleme Dağılımı Formülü

Orantı örnekleme dağılımındaki fark için seçilen örnekler binom dağılımlarıyla tanımlanır, çünkü pratik amaçlar için oran, başarılı vakaların toplam gözlem sayısına oranıdır.

Bununla birlikte, merkezi limit teoremi nedeniyle binom dağılımları normal olasılık dağılımlarına yaklaştırılabilir. Bu nedenle oranlardaki farkın örnekleme dağılımı, aşağıdaki özelliklerle normal bir dağılıma yaklaştırılabilir:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Not: Oranlardaki farkın örnekleme dağılımı ancak aşağıdaki durumlarda normal dağılıma yaklaşabilir:

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Dolayısıyla oranlardaki farkın örnekleme dağılımı normal bir dağılıma yakınlaştırılabileceğinden, oranlardaki farkın örnekleme dağılımının istatistiğini hesaplama formülü aşağıdaki gibidir:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Altın:

$\widehat{p_i}$

örnek oranı i’dir.
$p_i$

i nüfus oranıdır.
$q_i$

i popülasyonunun başarısızlık olasılığıdır,

$q_i=1-p_i$

.
$n_i$

örneklem büyüklüğü i’dir.
$Z$

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.

Bu formül, oranlar arasındaki fark için hipotez testi formülüne benzer.

Oranlar farkının örnekleme dağılımının somut örneği

Oranlar Farkı Örnekleme Dağılımı’nın tanımını ve formülünün ne olduğunu gördükten sonra, kavramı anlamayı tamamlamak için adım adım çözülmüş bir örneği aşağıda görebilirsiniz.

İki üretim tesisinin doğruluğunu analiz etmek istiyorsunuz; bir fabrika, üretilen parçaların yalnızca %5’inde kusur olacak şekilde üretim yaparken, başka bir fabrikanın hatalı parça yüzdesi %8 olacak şekilde üretim yapıyor. Birinci fabrikadan 200 parçalık bir numune ve ikinci fabrikadan da 280 parçalık bir numune alırsak, ilk üretim tesisindeki kusur yüzdesinin ikinci fabrikadaki kusur yüzdesinden daha büyük olma olasılığı nedir? üretme?

Sorunun tüm verilerini bilmeyi tamamlamak için öncelikle her fabrikanın iyi üretilen parçalarının oranını hesaplayacağız:

$\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}$

Eğer birinci fabrikadaki kusur oranı ikinci fabrikadaki kusur oranından büyükse bu, aşağıdaki denklemin doğru olacağı anlamına gelir:

$\widehat{p_1}-\widehat{p_2}>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”89″ style=”vertical-align: -4px;”> Dolayısıyla oranlardaki farklılığın örnekleme dağılım olasılığını belirlemek için yukarıdaki bölümde açıklanan formülü uygulamamız gerekir: <p class=$ $Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}=\cfrac{0-(0,05-0,08)}{\displaystyle\sqrt{\frac{0,05\cdot 0,95}{200}+\frac{0,08\cdot 0,92}{280}}}=1,34$

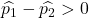
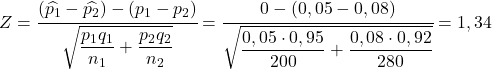
Dolayısıyla, birinci fabrikanın kusur oranının ikinci fabrikanın kusur oranından büyük olma olasılığı, Z değişkeninin 1,34’ten büyük olma olasılığına eşdeğerdir:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”> Son olarak, <a href=$ normal dağılım tablosunda karşılık gelen olasılığı aramamız yeterli; sorunu zaten çözmüş olacağız:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”> Kısaca birinci fabrikadaki kusur oranının ikinci fabrikadaki kusur oranından büyük olma olasılığı %9,01’dir. <div style=$ ➤ Bakınız: Ortalamalardaki farkın örnekleme dağılımı

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Oranlardaki farkın örneklem dağılımı nedir?

Oran Farkının Örnekleme Dağılımı Formülü

Oranlar farkının örnekleme dağılımının somut örneği

yazar hakkında

Dr.benjamin anderson

Yorum ekle